The complex number system:

PYQ-2023-Complex_Number-Q9

• $ z=a+i b$, then $a-i b$ is called conjugate of $z$ and is denoted by $\bar{z}$.

• Algebraic Form: If z = x + iy; then $|z| = \sqrt{x^2-y^2}$; $\bar{z} = x-iy $ and $\theta = \tan^{-1}(\frac{y}{x})$

• Polar Form: z = x + iy = r (cosθ + i sinθ ) = r cisθ where | z | = r ; principal value of z = θ .

• Exponential Form: For any complex number z = r (cosθ + i sinθ ), $z = r e^{iθ}$ is the exponential representation.

Equality in complex number:

$\quad z_{1}=z_{2} \Rightarrow \operatorname{Re}\left(z_{1}\right)=\operatorname{Re}\left(z_{2}\right)$ and $I_{m}\left(z_{1}\right)=I_{m}\left(z_{2}\right)$.

Representation of a complex number:

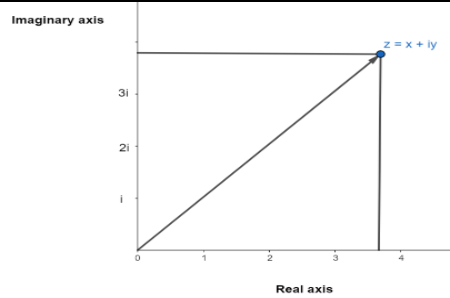
Properties of arguments:

• $\arg \left(z_{1} z_{2}\right)=\arg \left(z_{1}\right)+\arg \left(z_{2}\right)+2 m \pi$ for some integer $m$.

• $\arg \left(\frac{z_{1}}{ z_{2}}\right)=\arg \left(z_{1}\right)-\arg \left(z_{2}\right)+2 m \pi$ for some integer $m$.

• $\arg \left(z^{2}\right)=2 \arg (z)+2 m \pi$ for some integer $m$.

• $\arg (\mathrm{z})=0 \quad \Leftrightarrow \quad \mathrm{z}$ is a positive real number

• $\arg (\mathrm{z})= \pm \frac{\pi} {2 \Leftrightarrow \quad \mathrm{z}}$ is purely imaginary and $\mathrm{z} \neq 0$

Properties of conjugate:

PYQ-2023-Complex_Number-Q1, PYQ-2023-Complex_Number-Q2, PYQ-2023-Complex_Number-Q6, PYQ-2023-Complex_Number-Q7, PYQ-2023-Complex_Number-Q9

• $|z|=|\bar{z}|$

• $z \bar{z}=|z|^{2}$

• $\overline{z_{1}+z_{2}}=\bar{z}_1 + \bar{z}_2$

• $\overline{z_{1}-z_{2}}=\bar{z}_1 + \bar{z}_2$

• $\overline{z_{1} z_{2}}=\bar{z}_1 \bar{z}_2$

• $(\overline{\frac{z_1}{z_2}}) = \frac{\bar{z}_1}{\bar{z}_2} \quad (z_2 \neq 0)$

• $|z_1 + z_2|^2 = (z_1 + z_2) \overline{(z_1 + z_2) } = |z_1|^2 + |z_2|^2 + z_1 \bar{z}_2 + \bar{z}_1 z_2 $

• $\overline{\left(\bar{z}_{1}\right)}=z$

• If $w=f(z)$, then $\bar{w}=f(\bar{z})$

• $ \arg (\mathrm{z})+\arg (\overline{\mathrm{z}})$

• $z+\bar{z}=2 \operatorname{Re}(z)$

• $z-\bar{z}=2 i \operatorname{lm}(z)$

Rotation theorem:

$\quad $ If $P\left(z_{1}\right), Q\left(z_{2}\right)$ and $R\left(z_{3}\right)$ are three complex numbers and $\angle P Q R=\theta$, then

$$\left(\frac{z_{3}-z_{2}}{z_{1}-z_{2}}\right)=\left|\frac{z_{3}-z_{2}}{z_{1}-z_{2}}\right| e^{i \theta}$$

Demoivre’s theorem :

PYQ-2023-Complex_Number-Q1, PYQ-2023-Complex_Number-Q2

$\quad$ Case I : If $\mathrm{n}$ is any integer then

$\quad$ $(i)\hspace{1mm} (\cos \theta+i \sin \theta)^{\mathrm{n}}=\cos n \theta+i \sin n \theta$

$\quad$ $(ii)\hspace{1mm} (\cos \theta_{1} + i\sin \theta_{1})(\cos \theta_{2}+ i\sin \theta_{2})(\cos \theta_{3}+i \sin \theta_{3}) \ldots .(\cos \theta_{n}+i \sin \theta_{n}) = \cos (\theta_{1}+\theta_{2}+\theta_{3}+\ldots \ldots . . \theta_{n})+i \sin (\theta_{1}+\theta_{2}+\theta_{3}+\ldots .+\theta_{n})$

$\quad$ Case II : If $p, q \in Z$ and $q \neq 0$ then $(\cos \theta+i \sin \theta)^{p / q}=\cos \left(\frac{2 k \pi+p \theta}{q}\right)+i \sin \left(\frac{2 k \pi+p \theta}{q}\right)$ where $\mathrm{k}=0,1,2,3, \ldots \ldots, \mathrm{q}-1$

Cube root Of unity :

• The cube roots of unity are $1, \frac{-1+i \sqrt{3}}{2}, \frac{-1-i \sqrt{3}}{2}$

• If $\omega$ is one of the imaginary cube roots of unity then $1+\omega+\omega^{2}=0$. In general $1+\omega^{r}+\omega^{2 r}=0$; where $r \in I$ but is not the multiple of 3 .

Logarithm of a complex quantity :

$\quad \log _{e}(\alpha+i \beta)=\frac{1}{2} \log _{e}\left(\alpha^{2}+\beta^{2}\right)+i\left(2 n \pi+\tan ^{-1} \frac{\beta}{\alpha}\right) \text { where } n \in I . $

Geometrical properties:

PYQ-2023-Complex_Number-Q3, PYQ-2023-Complex_Number-Q4, PYQ-2023-Complex_Number-Q8, PYQ-2023-Complex_Number-Q10, PYQ-2023-Complex_Number-Q11

• Distance formula : $\left|z_{1}-z_{2}\right|$.

• Section formula : $z=\frac{m z_{2}+n z_{1}}{m+n}$ (internal division), $z=\frac{m z_{2}-n z_{1}}{m-n}$ (external division)

• $\operatorname{amp}(z)=\theta$ is a ray emanating from the origin inclined at an angle $\theta$ to the $x-$ axis

• $|z-a|=|z-b|$ is the perpendicular bisector of the line joining a to $b$.

• The equation of a line joining $z_{1}$ & $z_{2}$ is given by, $z=z_{1}+t\left(z_{1}-z_{2}\right)$ where $t$ is a real parameter.

• The equation of circle having centre $z_{0}$ & radius $\rho$ is:

$$\left|z-z_{0}\right|=\rho ~ \text{or}~ z \bar{z} - z_0 \bar{z} - \bar{z}_0 z + \bar{z}_0 z_0 - \rho^{2} = 0 ~ \text{ which is of the form} ~$$

$$\mathrm{z} \overline{\mathrm{z}}+\bar{\alpha} \mathrm{z}+\alpha \overline{\mathrm{z}}+\mathrm{k}=0, \mathrm{k} \text{~ is real. Centre is ~} \alpha ~\text{and radius}~ = \sqrt{\alpha \bar{\alpha}- k}$$

$\qquad \qquad$ Circle will be real if $\alpha \bar{\alpha}-\mathrm{k} \geq 0$..

• If $\left|z_{1}-z_{1}\right|+\left|z-z_{2}\right|=K>\left|z_{1}-z_{2}\right|$ then locus of $z$ is an ellipse whose focii are $z_{1}$ & $z_{2}$

• If $\left|\frac{z-z_{1}}{z-z_{2}}\right|=k \neq 1,0$, then locus of $z$ is circle.

• If ||$z-z_{1}|-| z-z_{2}||=K<\left|z_{1}-z_{2}\right|$ then locus of $z$ is a hyperbola, whose focii are $z_{1}$ & $z_{2}$

Algebra of complex numbers

PYQ-2023-Complex_Number-Q2, PYQ-2023-Complex_Number-Q4, PYQ-2023-Complex_Number-Q5, PYQ-2023-Complex_Number-Q6, PYQ-2023-Complex_Number-Q7, PYQ-2023-Complex_Number-Q11

• Addition: $(a+i b)+(c+i d)=(a+c)+i(b+d)$

• Subtraction: $(a+i b)-(c+i d)=(a-c)+i(b-d)$

• Multiplication: $(a+i b)(c+i d)=(a c-b d)+i(a d+b c)$

• Reciprocal: If at least one of $\mathrm{a}$, $\mathrm{b}$ is non-zero, then the reciprocal of $\mathrm{a}+\mathrm{ib}$ is given by

$$\frac{1}{a+i b}=\frac{a-i b}{(a+i b)(a-i b)}=\frac{a}{a^2+b^2}-i \frac{b}{a^2+b^2}$$

• Quotient: If at least one of c, d is non-zero, then quotient of a +ib and c +id is given by $$\frac{a+i b}{c+i d}=\frac{(a+i b)(c-i d)}{(c+i d)(c-i d)}=\frac{(a c+b d)+i(b c-a d)}{c^2+d^2}=\frac{a c+b d}{c^2+d^2}+i \frac{b c-a d}{c^2+d^2}$$

Properties of modulus:

PYQ-2023-Complex_Number-Q4, PYQ-2023-Complex_Number-Q11

• $|z| \geq 0 ;|z| \geq \operatorname{Re}(z) ;|z| \geq \operatorname{Im}(z) ;|z|=|\bar{z}|=|-z|$

• $z \bar{z}=|z|^2$; if $|z|=1$, then $z=\frac{1}{\bar{z}}$

• $\left|z_1 z_2\right|=\left|z_1\right| \cdot\left|z_2\right|$

• $\left|\frac{z_1}{z_1}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}, z_2 \neq 0$

• $\left|z^n\right|=|z|^n$

• $\left|z_1+z_2\right|^2+\left|z_1- z_2\right|^2=2\left[\left|z_1\right|^2+\left|z_2\right|^2\right]$

• ||$z_1|-| z_2|| \leq\left|z_1+z_2\right| \leq\left|z_1\right|+\left|z_2\right|$ [Triangle Inequality]

Properties of principal argument(Arg):

PYQ-2023-Complex_Number-Q7

• $ \operatorname{Arg}\left(z_1 \cdot z_2\right)=\operatorname{Arg} z_1+\operatorname{Arg} z_2+2 k \pi, k \in I$

• $ \operatorname{Arg}\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)=\operatorname{Arg} \mathrm{z}_1-\operatorname{Arg} z_2+2 \mathrm{k} \pi, k \in \mathrm{I}$

• $\operatorname{Arg}\left(z^n\right)=n \operatorname{Arg}(z)+2 k \pi$, where the value of $k$ should be such that RHS lies in $(-\pi, \pi]$

• Based on the above information, we have the following:

  • $|\operatorname{Re}(z)|+|\operatorname{Im}(z)| \leq \sqrt{2}|z|$

  • ||$z_1|-| z_2|| \leq\left|z_1-z_2\right| \leq\left|z_1\right|+\left|z_2\right|$. Thus $\left|z_1\right|+\left|z_2\right|$ is the greatest possible value of $\left|z_1+z_2\right|$ and ||$z_1|-| z_2||$ is the least possible value of $\left|z_1+z_2\right|$.

  • If $\left|z+\frac{1}{z}\right|=a$, the greatest and least values of $|z|$ are respectively $\frac{a+\sqrt{a^2+4}}{2}$ and $\frac{-a+\sqrt{a^2+4}}{2}$.

  • $\left|z_1+\sqrt{z_1^2-z_2^2}\right|+\left|z_2-\sqrt{z_1^2-z_2^2}\right|=\left|z_1+z_2\right|+\left|z_1-z_2\right|$

  • If $z_1=z_2 \Leftrightarrow\left|z_1\right|=\left|z_2\right|$ and $\arg z_1=\arg z_2$

  • $\left|z_1+z_2\right|=\left|z_1\right|+\left|z_2\right| \Leftrightarrow \arg \left(z_1\right)=\arg \left(z_2\right)$ i.e. $z_1$ and $z_2$ are parallel.

  • $\left|z_1+z_2\right|=\left|z_1\right|+\left|z_2\right| \Leftrightarrow \arg \left(z_1\right)-\arg \left(z_2\right)=2 n \pi$, where $n$ is some integer.

  • $\left|z_1-z_2\right|=|| z_1|-| z_2|| \Leftrightarrow \arg \left(z_1\right)-\arg \left(z_2\right)=2 n \pi$, where $n$ is some integer.

  • $\left|z_1+z_2\right|=\left|z_1-z_2\right| \Leftrightarrow \arg \left(z_1\right)-\arg \left(z_2\right)=(2 n+1) \frac{\pi}{2}$, where $n$ is some integer.

  • If $\left|z_1\right| \leq 1,\left|z_2\right| \leq 1$, then $\left|z_1+z_2\right|^2 \leq\left(\left|z_1\right|-\left|z_2\right|\right)^2+\left(\arg \left(z_1\right)-\arg \left(z_2\right)\right)^2$, and $ \left|z_1+z_2\right|^2 \geq\left(\left|z_1\right|+\left|z_2\right|\right)^2-\left(\arg \left(z_1\right)-\arg \left(z_2\right)\right)^2 $

Cube root of unity:

• The cube roots of unity are $1, \frac{-1+i \sqrt{3}}{2}, \frac{-1-i \sqrt{3}}{2}$

• If $\omega$ is one of the imaginary cube roots of unity then $1+\omega+\omega^2=0$.

$\quad$ $\quad$ In general $1+\omega^r+\omega^{2 r}=0$; where $r=1$, and not a multiple of 3 .

• In polar form the cube roots of unity are: $\cos 0+i \sin 0 ; \cos \frac{2 \pi}{3}+i \sin \frac{2 \pi}{3} ; \cos \frac{4 \pi}{3}+i \sin \frac{4 \pi}{3}$

• The three cube roots of unity when plotted on the argand plane constitute the vertices of an equilateral triangle.

$\quad \quad $ [Note that the 3 cube roots of $\mathrm{i}$ lies on the vertices of an isosceles triangle]

• The following factorization should be remembered.

  For $a, b, c \in R$ and $\omega$ being the cube root of unity,

  • $a^3-b^3=(a-b)(a-\omega b)\left(a-\omega^2 b\right)$

  • $x^2+x+1=(x-\omega)\left(x-\omega^2\right)$

  • $a^3+b^3=(a+b)(a+\omega b)\left(a+\omega^2 b\right)$

  • $\mathrm{a}^3+\mathrm{b}^3+\mathrm{c}^3-3 \mathrm{abc}=(\mathrm{a}+\mathrm{b}+\mathrm{c})\left(\mathrm{a}+\omega \mathrm{b}+\omega^2 \mathrm{c}\right)\left(\mathrm{a}+\omega^2 \mathrm{~b}+\omega \mathrm{c}\right)$

$n^{\text {th }}$ roots of unity:

$\quad$ If $1, \alpha_1, \alpha_2, \alpha_3, \ldots \ldots, \alpha_{n-1}$ are the $n, n^{\text {th }}$ roots of unity then,

• They are in G.P. with common ratio $\mathrm{e}^{i\left(\frac{2 \pi}{n}\right)}=\cos \frac{2 \pi}{n}+i \sin \frac{2 \pi}{n}$

• $1^{\mathrm{p}}+\alpha_1^{\mathrm{p}}+\alpha_2^{\mathrm{p}}+\ldots \ldots+\alpha_{\mathrm{n}-1}^{\mathrm{p}}=0$ if $\mathrm{p}$ is not an integral multiple of $\mathrm{n}$ $1^p+\left(\alpha_1\right)^p+\left(\alpha_2\right)^p+\ldots \ldots .+\left(\alpha_{n-1}\right)^p=n$ if $p$ is an integral multiple of $n$.

• $\left(1-\alpha_1\right)\left(1-\alpha_2\right) \ldots \ldots\left(1-\alpha_{n-1}\right)=n$.

Steps to determine nth roots of a complex number:

• Represent the complex number whose roots are to be determined in polar form.

• Add $2 m \pi$ to the argument.

• Apply De Moivre’s Theorem.

• Put m = 0, 1, 2, 3, ……. (n - 1) to get all the n-th roots.

Summation of series using complex number:

• $\cos \theta+\cos 2 \theta+\cos 3 \theta+\ldots \ldots+\cos n \theta=\frac{\sin \left(\frac{n \theta}{2}\right)}{\sin \left(\frac{\theta}{2}\right)} \cos \left(\frac{n+1}{2}\right) \theta$

• $\sin \theta+\sin 2 \theta+\sin 3 \theta+\ldots \ldots+\sin n \theta=\frac{\sin \left(\frac{\mathrm{n} \theta}{2}\right)}{\sin \left(\frac{\theta}{2}\right)} \sin \left(\frac{\mathrm{n}+1}{2}\right) \theta$

Equation of a straight line:

$\quad$ The general equation of a straight line is $\bar{a}z + a \bar{z} + b = 0$ where, a is non-zero complex number and b is a real number.

Equation of circle:

$\quad$ An equation of the circle with centre $z_0$ and radius r is $|z - z_0 |= r$ or $z = z_0 + r e^{i \theta}$ (parametric form)

Equation of ellipse:

PYQ-2023-Complex_Number-Q8

$\quad$ Complex number $z + \frac{1}{z}$ on the complex plane is a standard ellipse where | z | = a, where a ≠ 0, 1.

Triangle on complex plane:

$\quad$ In a $\triangle A B C$, the vertices $A, B$ and $C$ are represented by the complex numbers $z_{1}, z_{2}$ and $z_{3}$ respectively, then

• Centroid: The centroid ’ $G$ ’ is given by $\frac{z_{1}+z_{2}+z_{3}}{3}$. Refer to Fig for centroid.

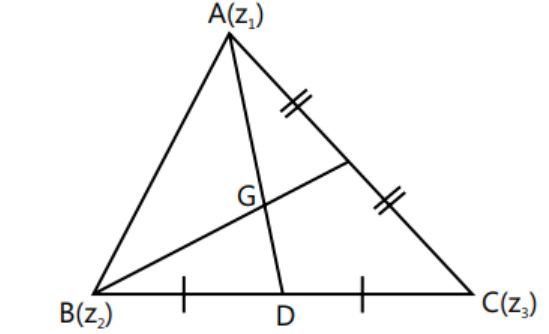
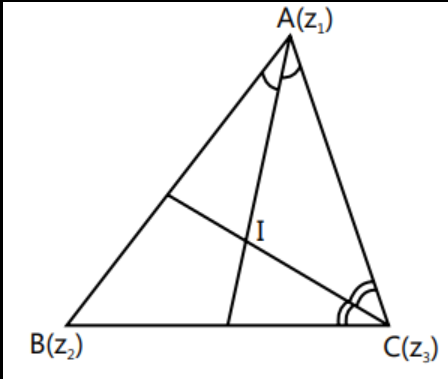
• Incentre: The incentre ’ $I$ ’ is given by $\frac{a z_{1}+b z_{2}+c z_{3}}{a+b+c}$. Refer to Fig for incentre .

• Orthocentre: The orhtocentre ’ $H$ ’ is given by $\frac{\mathrm{z} _{1} \tan A+\mathrm{z} _{2} \tan B+\mathrm{z} _{3} \tan C}{\sum \tan A}$

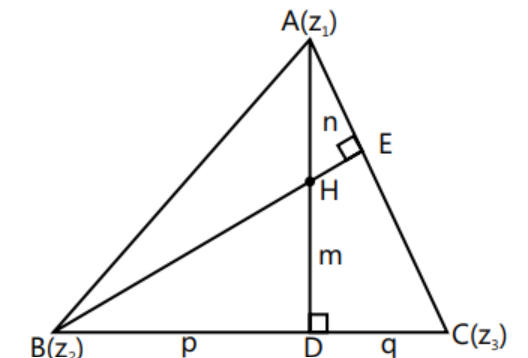
• Circumcentre:

$\quad$ Let $\mathrm{R}$ be the circumradius and the complex number $\mathrm{z}_{0}$ represent the circumcentre of the triangle as shown in the Figure.

$$\therefore\left|z_{1}-z_{0}\right|=\left|z_{2}-z_{0}\right|=\left|z_{3}-z_{0}\right|$$

$\quad$ Consider, $\left|z_{1}-z_{0}\right|^{2}=\left|z_{2}-z_{0}\right|^{2},$

$$ \begin{aligned} & \left(z _{1}-z _{0}\right)\left(\bar{z} _{1}-\bar{z} _{0}\right)=\left(z _{2}-z _{0}\right)\left(\bar{z} _{2}-\bar{z} _{0}\right) \\ & \overline{\mathrm{z}} _{1}\left(\mathrm{z} _{1}-\mathrm{z} _{0}\right)-\overline{\mathrm{z}} _{2}\left(\mathrm{z} _{2}-\mathrm{z} _{0}\right)=\overline{\mathrm{z}} _{0}\left[\left(\mathrm{z} _{1}-\mathrm{z} _{0}\right)-\left(\mathrm{z} _{2}-\mathrm{z} _{0}\right)\right] \\ & \overline{\mathrm{z}} _{1}\left(\mathrm{z} _{1}-\mathrm{z} _{0}\right)-\overline{\mathrm{z}} _{2}\left(\mathrm{z} _{2}-\mathrm{z} _{0}\right)=\overline{\mathrm{z}} _{0}\left(\mathrm{z} _{1}-\mathrm{z} _{2}\right) \end{aligned} $$

$\quad$ Similarly $1^{\text {st }}$ and $3^{\text {rd }}$ gives

$$\bar{z} _{1}\left(z _{1}-z _{0}\right)-\bar{z} _{3}\left(z _{3}-z _{0}\right)=\bar{z} _{0}\left(z _{1}-z _{3}\right)$$

$\quad$ On dividing (i) by (ii), $\bar{z} _{0}$ gets eliminated and we obtain $z _{0}$.

$\quad$ Alternatively: From Fig of circumcentre , we have

$$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{m}}{\mathrm{n}}=\frac{\text { Ar. } \triangle \mathrm{ABD}}{\text { Ar. } \triangle \mathrm{ADC}}=\frac{\text { Ar. } \triangle \mathrm{PBD}}{\text { Ar. } \triangle \mathrm{PDC}}$$

$$\therefore \frac{\mathrm{m}}{\mathrm{n}}=\frac{\text { Ar. } \triangle \mathrm{ABD}-\mathrm{Ar} \cdot \triangle \mathrm{PBD}}{\text { Ar. } \triangle \mathrm{ADC}-\mathrm{Ar} \cdot \Delta \mathrm{PDC}}=\frac{\Delta_{3}}{\Delta_{2}}$$

$$\therefore \frac{m}{n}=\frac{\frac{R^{2}}{2} \sin 2 C}{\frac{R^{2}}{2} \sin 2 B}=\frac{\sin 2 C}{\sin 2 B}$$

$\quad$ Hence, $Z_{D}=\frac{\sin 2 B\left(Z_{2}\right)+\sin 2 C\left(Z_{3}\right)}{\sin 2 B+\sin 2 C}$

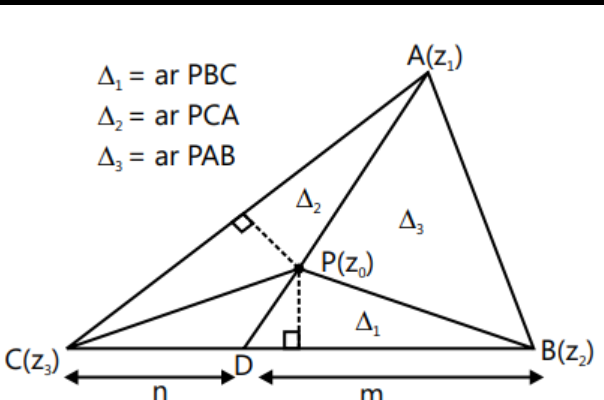
$\quad$ Now,

$$\frac{\mathrm{PA}}{\mathrm{PD}}=\frac{l}{\mathrm{k}}=\frac{\Delta \mathrm{ABP}}{\Delta \mathrm{PBD}}=\frac{\Delta \mathrm{APC}}{\triangle \mathrm{CPD}}=\frac{\Delta \mathrm{ABP}+\Delta \mathrm{APC}}{\Delta \mathrm{PBD}+\Delta \mathrm{CPD}} \therefore \frac{l}{\mathrm{k}}=\frac{\Delta_{3}+\Delta_{2}}{\Delta_{1}}=\frac{\sin 2 \mathrm{C}+\sin 2 \mathrm{~B}}{\sin 2 \mathrm{~A}}$$

$\quad$ Hence,

$$\mathrm{z} _{0}=\frac{\mathrm{kz _{1 }}+l \mathrm{z} _{\mathrm{D}}}{\mathrm{k}+l}=\frac{\mathrm{z} _{1} \sin 2 \mathrm{~A}+\mathrm{z} _{2} \sin 2 \mathrm{~B}+\mathrm{z} _{3} \sin 2 \mathrm{C}}{\sum \sin 2 \mathrm{~A}}$$

More results of triangle on complex plane:

• The area of the triangle whose vertices are $z_{1} i z$ and $z+i z$ is $\frac{1}{2}|z|^{2}$.

• The area of the triangle with vertices $z_{1} \omega z$ and $z+\omega z$ is $\frac{\sqrt{3}}{4}|z|^{2}$.

• If $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}$ be the vertices of an equilateral triangle and $\mathrm{z} _{0}$ be the circumcentre, then $\mathrm{z} _{1}^{2}+\mathrm{z} _{2}^{2}+\mathrm{z} _{3}^{2}=3 \mathrm{z} _{0}^{2}$.

• If $z_{1}, z_{2}, z_{3}, \ldots \ldots z_{n}$ be the vertices of a regular polygon of $n$ sides and $z_{0}$ be its centroid, then $z_{1}^{2}+z_{2}^{2}+\ldots \ldots+z_{n}^{2}=n z_{0}^{2}$.

• If $z_{1}, z_{2}, z_{3}$ be the vertices of a triangle, then the triangle is equilateral if

$\quad \left(z_{1}-z_{2}\right)^{2}+\left(z_{2}-z_{3}\right)^{2}+\left(z_{3}-z_{1}\right)^{2}=0$ or $z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}$ or $\frac{1}{z_{1}-z_{2}}+\frac{1}{z_{2}-z_{3}}+\frac{1}{z_{3}-z_{1}}=0$.

• If $z_{1}, z_{2}, z_{3}$ are the vertices of an isosceles triangle, right angled at $z_{2}$ then $z_{1}^{2}+2 z_{2}^{2}+z_{3}^{2}=2 z_{2}\left(z_{1}+z_{3}\right)$.

• If $z_{1}, z_{2}, z_{3}$ are the vertices of a right-angled isosceles triangle, then $\left(z_{1}-z_{2}\right)^{2}=2\left(z_{1}-z_{3}\right)\left(z_{3}-z_{2}\right)$.

• If $z_{1}, z_{2}, z_{3}$ be the affixes of the vertices $A, B, C$ respectively of a triangle $A B C$, then its orthocentere is $$\frac{a(\sec A) z_{1}+b(\sec B) z_{2}+c(\sec C) z_{3}}{a \sec A+b \sec B+c \sec C}$$