SATHEE: System of Particles and Rotational Motion

System of Particles and Rotational Motion - Result Question 53

57. From a disc of radius $R$ and mass $M$ , a circular hole of diameter $R$ , whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

[2016]

(a) $15 M R^{2} / 32$

(b) $13 M R^{2} / 32$

(d) $9 M R^{2} / 32$

Show Answer

Answer:

Correct Answer: 57. (b)

Solution:

(b) Moment of inertia of complete disc about point ’ $O$ ‘.

$I_{Total disc} = \frac{M R^{2}}{2}$

Mass of removed disc

$M_{Removed} = \frac{M}{4}$ (Mass $\propto$ area $)$

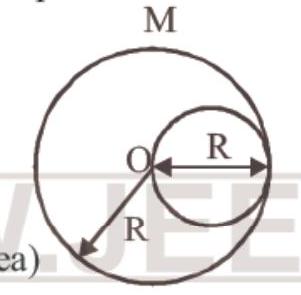
Moment of inertia of removed disc about point ‘O’.

$I_{Removed}$ (about same perpendicular axis)

$= I_{c m} + m x^{2}$

$= \frac{M}{4} \frac{(R / 2)^{2}}{2} + \frac{M}{4} (\frac{R}{2})^{2} = \frac{3 M R^{2}}{32}$

Therefore the moment of inertia of the remaining part of the disc about a perpendicular axis passing through the centre,

$I_{Remaing disc} = I_{Total} - I_{Removed}$

$= \frac{M R^{2}}{2} - \frac{3}{32} M R^{2} = \frac{13}{32} M R^{2}$

Moment of inertia of a part of a rigid body (Symmetrically cut from the whose mass) is the same as that of the whole body when whole mass is replaced by mass of that part.

System of Particles and Rotational Motion - Result Question 53

57. From a disc of radius $R$ and mass $M$ , a circular hole of diameter $R$ , whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

System of Particles and Rotational Motion - Result Question 53

57. From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

57. From a disc of radius $R$ and mass $M$ , a circular hole of diameter $R$ , whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?