System of Particles and Rotational Motion - Result Question 53
57. From a disc of radius $R$ and mass $M$, a circular hole of diameter $R$, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
[2016]
(a) $15 MR^{2} / 32$
(c) $11 MR^{2} / 32$
(b) $13 MR^{2} / 32$
(d) $9 MR^{2} / 32$
Show Answer
Answer:
Correct Answer: 57. (b)
Solution:
- (b) Moment of inertia of complete disc about point ’ $O$ ‘.
$I _{\text{Total disc }}=\frac{MR^{2}}{2}$
Mass of removed disc
$M _{\text{Removed }}=\frac{M}{4}$ (Mass $\propto$ area $)$
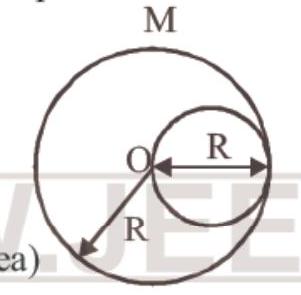
Moment of inertia of removed disc about point ‘O’.
$I _{\text{Removed }}$ (about same perpendicular axis)
$=I _{cm}+mx^{2}$
$=\frac{M}{4} \frac{(R / 2)^{2}}{2}+\frac{M}{4}(\frac{R}{2})^{2}=\frac{3 MR^{2}}{32}$
Therefore the moment of inertia of the remaining part of the disc about a perpendicular axis passing through the centre,
$I _{\text{Remaing disc }}=I _{\text{Total }}-I _{\text{Removed }}$
$=\frac{MR^{2}}{2}-\frac{3}{32} MR^{2}=\frac{13}{32} MR^{2}$
Moment of inertia of a part of a rigid body (Symmetrically cut from the whose mass) is the same as that of the whole body when whole mass is replaced by mass of that part.










