Ray Optics and Optical Instruments - Result Question 26
26. Two similar thin equi-convex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is
(a)
(b)
(c)
(d)
[2019]
Show Answer
Answer:
Correct Answer: 26. (b)
Solution:
- (b)
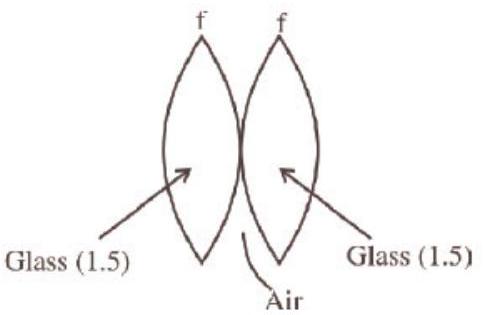
Equivalent focal length in air
When glycerin is filled inside, it behaves like a concave lens of focal length (-f)
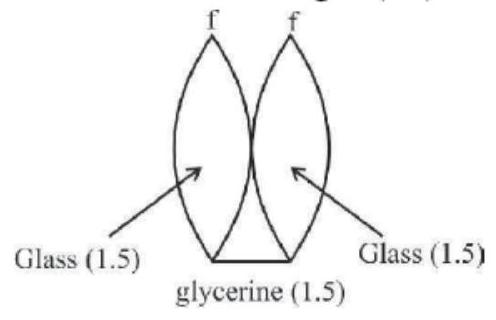
Dividing (i) by (ii), we get






