Ray Optics and Optical Instruments - Result Question 26
«««< HEAD:content/english/neet-pyq-chapterwise/physics/ray-optics-and-optical-instruments/ray-optics-and-optical-instruments-result-question-26.md
26. Two similar thin equi-convex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is $F_1$. When the space between the two lenses is filled with glycerin (which has the same refractive index ( $=1.5)$ as that of glass) then the equivalent focal length is $F_2$. The ratio $F_1: F_2$ will be:
======= ####26. Two similar thin equi-convex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is $F_1$. When the space between the two lenses is filled with glycerin (which has the same refractive index ( $=1.5)$ as that of glass) then the equivalent focal length is $F_2$. The ratio $F_1: F_2$ will be:
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/ray-optics-and-optical-instruments/ray-optics-and-optical-instruments—result-question-26.md (a) $2: 1$
(b) $1: 2$
(c) $2: 3$
(d) $3: 4$
[2019]
Show Answer
Answer:
Correct Answer: 26. (b)
Solution:
- (b)
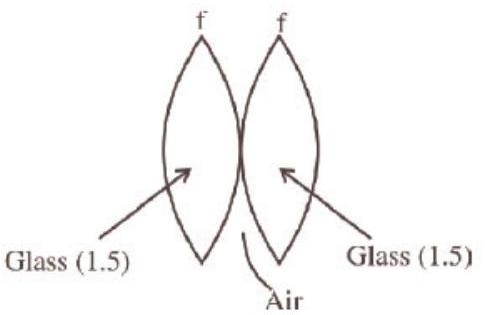
Equivalent focal length in air
$\frac{1}{F_1}=\frac{1}{f}+\frac{1}{f}=\frac{2}{f}$
$\Rightarrow F_1=\frac{f}{2}$
When glycerin is filled inside, it behaves like a concave lens of focal length (-f)
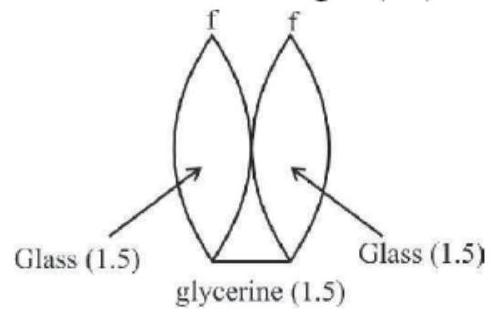
$\therefore \frac{1}{F_2}=\frac{1}{f}+\frac{1}{f}-\frac{1}{f} \quad \Rightarrow F_2=f$
Dividing (i) by (ii), we get
$\frac{F_1}{F_2}=\frac{1}{2}$










