Gravitation - Result Question 3
3. The figure shows elliptical orbit of a planet
[2009]
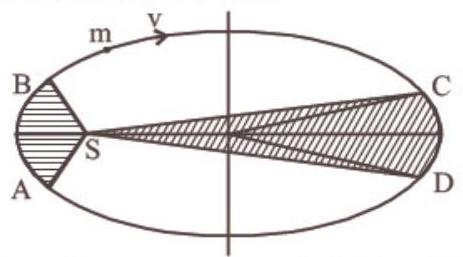
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- (b) According to Kepler’s law, the areal velocity of a planet around the sun always remains constant.
The area covered by radius vector in
It follows that speed of the planet is maximum when it is closest to the sun and is minimum when the planet is farthest from the sun.






