Gravitation - Result Question 3
3. The figure shows elliptical orbit of a planet $m$ about the sun $S$. The shaded area SCD is twice the shaded area $S A B$. If $t_1$ is the time for the planet to move from $C$ to $D$ and $t_2$ is the time to move from $A$ to $B$ then :
[2009]
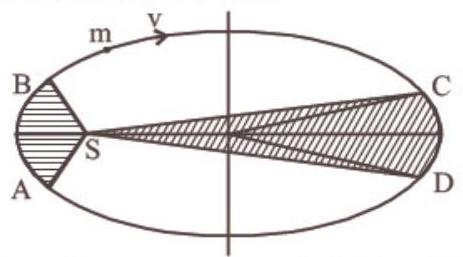
(a) $t_1=4 t_2$
(b) $t_1=2 t_2$
(c) $t_1=t_2$
(d) $t_1>t_2$
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- (b) According to Kepler’s law, the areal velocity of a planet around the sun always remains constant.
$SCD: A_1-t_1$ (areal velocity constant)
$SAB: A_2-t_2$
$\frac{A_1}{t_1}=\frac{A_2}{t_2}$,
$t_1=t_2 \cdot \frac{A_1}{A_2} \quad(.$ given $.A_1=2 A_2)$
$ \begin{aligned} & =t_2 \cdot \frac{2 A_2}{A_2} \\ & \therefore \quad t_1=2 t_2 \end{aligned} $
The area covered by radius vector in $d t$ seconds $=$
$\frac{1}{2} r^{2} d \theta$
$ \begin{gathered} \text{ Area velocity }=\frac{1}{2} r^{2} \frac{d \theta}{d t}=\frac{1}{2} r^{2} \omega \quad(\because \omega \frac{d \theta}{d t}) \\ =\frac{1}{2} r v \quad(\because v=\omega r) \end{gathered} $
It follows that speed of the planet is maximum when it is closest to the sun and is minimum when the planet is farthest from the sun.










