Dual Nature of Radiation and Matter - Result Question 4
4. An electron of mass $m$ with an initial velocity $\vec{V}=V_0 \hat{i} \quad(V_0>0)$ enters an electric field $\vec{E}=-E_0 \hat{i}(E_0=.$ constant $.>0)$ at $t=0$. If $\lambda_0$ is its de-Broglie wavelength initially, then its deBroglie wavelength at time $t$ is [2018]
«««< HEAD
======= ####4. An electron of mass $m$ with an initial velocity $\vec{V}=V_0 \hat{i} \quad(V_0>0)$ enters an electric field $\vec{E}=-E_0 \hat{i}(E_0=.$ constant $.>0)$ at $t=0$. If $\lambda_0$ is its de-Broglie wavelength initially, then its deBroglie wavelength at time $t$ is [2018]
c3eec34ec6b1fad69db54a20ad4b2dca40c2aa54 (a) $\frac{\lambda_0}{(1+\frac{e E_0}{m V_0} t)}$
(b) $\lambda_0(1+\frac{e E_0}{m V_0} t)$
(c) $\lambda_0$
(d) $\lambda_0 t$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- (a) Initial de-Brogile wavelength
$ \begin{equation*} \lambda_0=\frac{h}{m V_0} \tag{i} \end{equation*} $
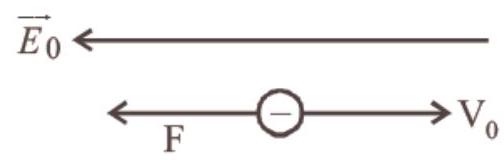
Acceleration of electron
$ a=\frac{e E_0}{m} \quad(\because F=m a=e E_0) $
Velocity after time ’ $t$ '
$ \begin{aligned} V & =(V_0+\frac{e E_0}{m} t) \\ \text{ So, } \lambda & =\frac{h}{m V}=\frac{h}{m(V_0+\frac{e E_0}{m} t)} \end{aligned} $
$ \begin{equation*} =\frac{h}{m V_0[1+\frac{e E_0}{m V_0} t]}=\frac{\lambda_0}{[1+\frac{e E_0}{m V_0} t]} \tag{ii} \end{equation*} $
Dividing eqs. (ii) by (i),
de-Broglie wavelength $\lambda=\frac{\lambda_0}{[1+\frac{e E_0}{m V_0} t]}$






