Atoms - Result Question 18
19. Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelength $\lambda_1: \lambda_2$ emitted in the two cases is
«««< HEAD
======= ####19. Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelength $\lambda_1: \lambda_2$ emitted in the two cases is
c3eec34ec6b1fad69db54a20ad4b2dca40c2aa54 (a) $7 / 5$
(b) $27 / 20$
(c) $27 / 5$
(d) $20 / 7$
[2012]
Show Answer
Answer:
Correct Answer: 19. (d)
Solution:
- (d)
$n=1$ (excited state)
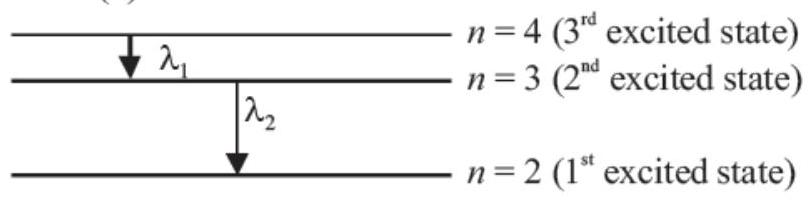
According to Rydberg formula
$\frac{1}{\lambda}=R[\frac{1}{n_f^{2}}-\frac{1}{n_i^{2}}]$
In first case, $n_f=3, n_i=4$
$\therefore \frac{1}{\lambda_1}=R[\frac{1}{3^{2}}-\frac{1}{4^{2}}]=R[\frac{1}{9}-\frac{1}{16}]=\frac{7}{144} R$ In second case, $n_f=2, n_i=3$
$\therefore \frac{1}{\lambda_2}=R[\frac{1}{2^{2}}-\frac{1}{3^{2}}]=R[\frac{1}{4}-\frac{1}{9}]=\frac{5}{36} R$
Divide (ii) by (i), we get
$\frac{\lambda_1}{\lambda_2}=\frac{5}{36} \times \frac{144}{7}=\frac{20}{7}$
