Atoms - Result Question 18
«««< HEAD:content/english/neet-pyq-chapterwise/physics/atoms/atoms-result-question-18.md
19. Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelength $\lambda_1: \lambda_2$ emitted in the two cases is
======= ####19. Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelength $\lambda_1: \lambda_2$ emitted in the two cases is
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/atoms/atoms—result-question-18.md (a) $7 / 5$
(b) $27 / 20$
(c) $27 / 5$
(d) $20 / 7$
[2012]
Show Answer
Answer:
Correct Answer: 19. (d)
Solution:
- (d)
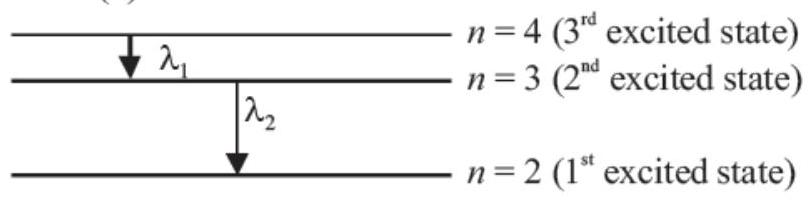
$n=1$ (excited state)
According to Rydberg formula
$\frac{1}{\lambda}=R[\frac{1}{n_f^{2}}-\frac{1}{n_i^{2}}]$
In first case, $n_f=3, n_i=4$
$\therefore \frac{1}{\lambda_1}=R[\frac{1}{3^{2}}-\frac{1}{4^{2}}]=R[\frac{1}{9}-\frac{1}{16}]=\frac{7}{144} R$ In second case, $n_f=2, n_i=3$
$\therefore \frac{1}{\lambda_2}=R[\frac{1}{2^{2}}-\frac{1}{3^{2}}]=R[\frac{1}{4}-\frac{1}{9}]=\frac{5}{36} R$
Divide (ii) by (i), we get
$\frac{\lambda_1}{\lambda_2}=\frac{5}{36} \times \frac{144}{7}=\frac{20}{7}$










