Solution

A loaded die is thrown such that

$P(1)=P(2)=0.2, P(3)=P(5)=P(6)=0.1$ and $P(4)=0.3$ and die is thrown two times. Also given that:

$A=$ Same number each time and

$B=$ Total score is 10 or more.

$ \begin{aligned} & \text{ So, } P(A)=[P(1,1)+P(2,2)+P(3,3)+P(4,4)+P(5,5)+P(6,6)] \\ & =P(1) \cdot P(1)+P(2) \cdot P(2)+P(3) \cdot P(3)+P(4) \cdot P(4) \\ & +P(5) \cdot P(5)+P(6) \cdot P(6) \\ & =0.2 \times 0.2+0.2 \times 0.2+0.1 \times 0.1+0.3 \times 0.3+0.1 \times 0.1 \\ & +0.1 \times 0.1 \\ & =0.04+0.04+0.01+0.09+0.01+0.01=0.20 \end{aligned} $

Now $B=[(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)]$

$P(B)=[P(4) \cdot P(6)+P(6) \cdot P(4)+P(5) \cdot P(5)+P(5) \cdot P(6)$ $+P(6) \cdot P(5)+P(6) \cdot P(6)$

$=0.3 \times 0.1+0.1 \times 0.3+0.1 \times 0.1+0.1 \times 0.1+0.1 \times 0.1$ $+0.1 \times 0.1$

$=0.03+0.03+0.01+0.01+0.01+0.01=0.10$

$A$ and $B$ both events will be independent if

$$ \begin{equation*} P(A \cap B)=P(A) \cdot P(B) \tag{i} \end{equation*} $$

Here,

$ (A \cap B)={(5,5),(6,6)} $

$ \therefore \quad P(A \cap B)=P(5,5)+P(6,6)=P(5) \cdot P(5)+P(6) \cdot P(6) $

$ =0.1 \times 0.1+0.1 \times 0.1=0.02 $

From eq. (i) we get

$ \begin{aligned} & 0.02=0.20 \times 0.10 \\ & 0.02=0.02 \end{aligned} $

Hence, $A$ and $B$ are independent events.

Solution

According to the solution of Q. 1 , we have

$A={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}$

$\therefore n(A)=6$ and $n(S)=6 \times 6=36$

So, $P(A)=\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}$

and $\quad B={(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)}$

$n(B)=6$ and $n(S)=36$

$\therefore \quad P(B)=\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}$

$A \cap B={(5,5),(6,6)}$

$\therefore P(A \cap B)=\frac{2}{36}=\frac{1}{18}$

Therefore, if $A$ and $B$ are independent, then

$P(A \cap B)=P(A) \cdot P(B)$

$\Rightarrow \quad \frac{1}{18} \neq \frac{1}{6} \times \frac{1}{6} \Rightarrow \frac{1}{18} \neq \frac{1}{36}$

Hence, $A$ and $B$ are not independent events.

Solution

We know that:

$A \cup B$ denotes that atleast one of the events occurs and $A \cap B$ denotes that the two events occur simultaneously.

$ \begin{matrix} \text{ So, } P(A \cup B) =P(A)+P(B)-P(A \cap B) \\ \Rightarrow 0.6 =P(A)+P(B)-0.3 \\ \Rightarrow 0.9 =P(A)+P(B) \\ \Rightarrow 0.9 =1-P(\overline{A})+1-P(\overline{B}) \\ \Rightarrow P(\overline{A})+P(\overline{B}) =2-0.9=1.1 \end{matrix} $

Hence, the required answer is 1.1.

Solution

Let red marbles be represented with $R$ and black marble with B. The following three conditions are possible, if atleast one of the three marbles drawn be black and the first marble is red.

(i) $E_1$ : II ball is black and III is red

(ii) $E_2$ : II ball is black and III is also black

(iii) $E_3:$ II ball is red and III is black

$ \begin{aligned} & \therefore \quad P(E_1)=P(R_1) \cdot P(B_1 / R_1) \cdot P(R_2 / R_1 B_1)=\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{4}{6}=\frac{60}{336}=\frac{5}{28} \\ & \quad P(E_2)=P(R_1) \cdot P(B_1 / R_1) \cdot P(B_2 / R_1 B_1)=\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{2}{6}=\frac{30}{336}=\frac{5}{56} \\ & \text{ and } P(E_3)=P(R_1) \cdot P(R_2 / R_1) \cdot B(B_1 / R_1 R_2)=\frac{5}{8} \cdot \frac{4}{7} \cdot \frac{3}{6}=\frac{60}{336}=\frac{5}{28} \\ & \therefore \quad P(E)=P(E_1)+P(E_2)+P(E_3)=\frac{5}{28}+\frac{5}{56}+\frac{5}{28}=\frac{25}{56} \end{aligned} $

Hence the required probability is $\frac{25}{56}$.

Solution

Two dice are thrown together

$\therefore n(S)=36$

$E=\text{ A total of } 4={(2,2),(1,3),(3,1)} \quad \therefore n(E)=3$

$F=\text{ A total of } 9 \text{ or more } $

$=\{(3,6),(6,3),(5,4),(4,5),(5,5),(4,6),(6,4),(5,6),(6,5),(6,6)\}$

$\therefore n(F)=10 ; G=\text{ A total divisible by } 5 $

$={(1,4),(4,1),(2,3),(3,2),(4,6),(6,4),(5,5)} \therefore n(G)=7$

Here, we see that $(E \cap F)=\phi$ and $(E \cap G)=\phi$

and $ (F \cap G)={(4,6),(6,4),(5,5)} $

$ \begin{aligned} \therefore \quad n(F & \cap G)=3 \text{ and }(E \cap F \cap G)=\phi \\ \therefore \quad P(E) & =\frac{n(E)}{n(S)}=\frac{3}{36}=\frac{1}{12} \\ P(F) & =\frac{n(F)}{n(S)}=\frac{10}{36}=\frac{5}{18} ; P(G)=\frac{n(G)}{n(S)}=\frac{7}{36} \\ P(F \cap G) & =\frac{3}{36}=\frac{1}{12} \text{ and } P(F) \cdot P(G)=\frac{5}{18} \cdot \frac{7}{36}=\frac{35}{648} \end{aligned} $

Since, $P(F \cap G) \neq P(F) . P(G)$

Hence, there is no pair of independent events.

Solution

We know that random variable $X$ takes values $0,1,2,3, \ldots, n$ is said to be binomial distribution having parameters $n$ and $p$, if the probability is given by $P(X=r)={ }^{n} C_r p^{r} q^{n-r}$, where $q=1-p$ and $r=0,1,2,3, \ldots$

Similarly in case of tossing a coin 3 times,

$n=3$ and $X$ has the values $0,1,2,3$ with $p=\frac{1}{2}, q=\frac{1}{2}$.

Hence, it is said to have a binomial distribution.

Solution

We have $P(A)=\frac{1}{2}, P(B)=\frac{1}{3}$ and $P(A \cap B)=\frac{1}{4}$

$ \begin{aligned} P(A^{\prime}) & =1-\frac{1}{2}=\frac{1}{2}, P(B^{\prime})=1-\frac{1}{3}=\frac{2}{3} \\ P(A^{\prime} \cap B^{\prime}) & =1-P(A \cup B)=1-[P(A)+P(B)-P(A \cap B)] \\ & =1-[\frac{1}{2}+\frac{1}{3}-\frac{1}{4}]=1-[\frac{6+4-3}{12}]=1-\frac{7}{12}=\frac{5}{12} \end{aligned} $

(i) $P(A / B)=\frac{P(A \cap B)}{P(B)}=\frac{1 / 4}{1 / 3}=\frac{3}{4}$

(ii) $P(B / A)=\frac{P(A \cap B)}{P(A)}=\frac{1 / 4}{1 / 2}=\frac{1}{2}$

(iii) $P(A^{\prime} / B)=\frac{P(A^{\prime} \cap B)}{P(B)}=\frac{P(B)-P(A \cap B)}{P(B)}$

$ =1-\frac{P(A \cap B)}{P(B)}=1-\frac{1 / 4}{1 / 3}=1-\frac{3}{4}=\frac{1}{4} $

(iv) $P(A^{\prime} / B^{\prime})=\frac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\frac{5 / 12}{2 / 3}=\frac{5}{12} \times \frac{3}{2}=\frac{5}{8}$

Solution

We have $P(A)=\frac{2}{5}, P(B)=\frac{1}{3}$ and $P(C)=\frac{1}{2}$

$ \begin{aligned} & P(A \cap C)=\frac{1}{5} \text{ and } P(B \cap C)=\frac{1}{4} \\ & \therefore \quad P(C / B)=\frac{P(B \cap C)}{P(B)}=\frac{1 / 4}{1 / 3}=\frac{3}{4} \\ & P(A^{\prime} \cap C^{\prime})=1-P(A \cup C) \\ & =1-[P(A)+P(C)-P(A \cap C)] \end{aligned} $

$ =1-[\frac{2}{5}+\frac{1}{2}-\frac{1}{5}]=1-\frac{7}{10}=\frac{3}{10} $

Hence, the required probabilities are $\frac{3}{4}$ and $\frac{3}{10}$.

Solution

Here,

$ P(E_1)=p_1 \text{ and } P(E_2)=p_2 $

(i)

$ p_1 p_2=P(E_1) \cdot P(E_2)=P(E_1 \cap E_2) $

So, $E_1$ and $E_2$ occur.

(ii)

$ (1-p_1) \cdot p_2=P(E_1)^{\prime} \cdot P(E_2)=P(E_1^{\prime} \cap E_2) $

So, $E_1$ does not occur but $E_2$ occurs.

(iii) $1-(1-p_1)(1-p_2)=1-P(E_1)^{\prime} P(E_2)^{\prime}=1-P(E_1^{\prime} \cap E_2^{\prime})$

$ =1-[1-P(E_1 \cup E_2)]=P(E_1 \cup E_2) $

So, either $E_1$ or $E_2$ or both $E_1$ and $E_2$ occur.

(iv)

$ \begin{aligned} p_1+p_2-2 p_1 p_2 & =P(E_1)+P(E_2)-2 P(E_1) \cdot P(E_2) \\ & =P(E_1)+P(E_2)-2 P(E_1 \cap E_2) \\ & =P(E_1 \cup E_2)-2 P(E_1 \cap E_2) \end{aligned} $

So, either $E_1$ or $E_2$ occurs but not both.

Solution

For a probability distribution, we know that if $P_i \geq 0$

(i) $\sum _{i=1}^{n} P_i=1 \Rightarrow k+k^{2}+2 k^{2}+k=1$

$ \begin{aligned} & \Rightarrow \quad 3 k^{2}+2 k-1=0 \Rightarrow 3 k^{2}+3 k-k-1=0 \\ & \Rightarrow \quad 3 k(k+1)-1(k+1)=0 \Rightarrow(3 k-1)(k+1)=0 \\ & \therefore \quad k=\frac{1}{3} \text{ and } k=-1 \end{aligned} $

But $k \geq 0 \quad \therefore k=\frac{1}{3}$

(ii) Mean of the distribution

$ E(X)=\sum _{i=1}^{n} X_i P_i=0.5 k+1 . k^{2}+1.5(2 k^{2})+2 k $

Solution

(i) To prove: $P(A)=P(A \cap B)+P(A \cap \overline{B})$ R.H.S. $=P(A \cap B)+P(A \cap \bar{{}B})$

$ \begin{aligned} & =P(A) \cdot P(B)+P(A) \cdot P(\overline{B})=P(A)[P(B)+P(\overline{B})] \\ & =P(A) \cdot 1 \\ & =P(A)=\text{ L.H.S. Hence proved. } \end{aligned} $

(ii) To prove: $P(A \cup B)=P(A \cap B)+P(A \cap \overline{B})+P(\overline{A} \cap B)$

R.H.S. $=P(A) \cdot P(B)+P(A) \cdot P(\bar{{}B})+P(\bar{{}A}) \cdot P(B)$

$ \begin{aligned} & =P(A) \cdot P(B)+P(A)[1-P(B)]+[1-P(A)] \cdot P(B) \\ & =P(A) \cdot P(B)+P(A)-P(A) \cdot P(B)+P(B)-P(A) \cdot P(B) \\ & =P(A)+P(B)-P(A \cap B) \\ & =P(A \cup B)=\text{ L.H.S. Hence proved. } \end{aligned} $

Solution

Given that: $X=0,1,2,3$

$\therefore P(X=r)={ }^{n} C_r p^{r} q^{n-r}$

where $n=3, p=\frac{1}{2}, q=\frac{1}{2}$ and $r=0,1,2,3$

$P(X=0)=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8} ; P(X=1)=3 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{3}{8}$

$P(X=2)=3 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{3}{8} ; P(X=3)=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}$

Probability distribution table is:

$\begin{array}{|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 \\ \hline P(X) & \frac{1}{8} & \frac{3}{8} & \frac{3}{8} & \frac{1}{8} \\ \hline \end{array}$

$ \begin{aligned} & E(X)=0+1 \times \frac{3}{8}+2 \times \frac{3}{8}+3 \times \frac{1}{8}=\frac{3}{8}+\frac{6}{8}+\frac{3}{8}=\frac{12}{8}=\frac{3}{2} \\ & E(X^{2})=0+1 \times \frac{3}{8}+4 \times \frac{3}{8}+9 \times \frac{1}{8}=\frac{3}{8}+\frac{12}{8}+\frac{9}{8}=\frac{24}{8}=3 \end{aligned} $

We know that $Var(X)=E(X^{2})-[E(X)]^{2}=3-(\frac{3}{2})^{2}=3-\frac{9}{4}=\frac{3}{4}$

$\therefore$ Standard deviation $=\sqrt{Var(X)}=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}$.

Solution

Let $X$ be the random variable of profit per throw.

$\begin{array}{|l|l|l|l|l|} \hline X & -1 & 1 & 4 \\ \hline P(X) & \frac{1}{2} & \frac{1}{2} & \frac{1}{6} \\ \hline \end{array}$

Since, she loses ₹ 1 for getting any of 2, 4, 5 .

So, $P(X=-1)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{3}{6}=\frac{1}{2}$

$ \begin{matrix} P(X=1)=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3} & (\because \text{ die showing } 1 \text{ or } 6) \\ P(X=4)=\frac{1}{6} & (\because \text{ die shows only a } 3) \end{matrix} $

Player’s expected profit $=\sum p_1 x_i$

$ =-1 \times \frac{1}{2}+1 \times \frac{1}{3}+4 \times \frac{1}{6}=-\frac{1}{2}+\frac{1}{3}+\frac{2}{3}=\frac{1}{2}=₹ 0.50 $

Solution

The dice is thrown three times

$\therefore$ Sample space $n(S)=(6)^{3}=216$

Let $E_1$ be the event when the sum of numbers on the dice was six and $E_2$ be the event when three two’s occur.

$ \begin{aligned} \Rightarrow E_1=\{(1,1,4),(1,2,3),(1,3,2),(1,4,1),(2,1,3),(2,2,2),(2,3,1),(3,1,2),\\(3,2,1),(4,1,1)\}[\therefore E_2=\{2,2,2\}] \end{aligned} $

$\begin{aligned}\Rightarrow n(E_1)=10 \text{ and } n(E_2)=1\end{aligned}$

$\begin{aligned}\therefore P(E_2 / E_1)=\frac{P(E_1 \cap E_2)}{P(E_1)}=\frac{1 / 216}{10 / 216}=\frac{1}{10} . \end{aligned} $

Solution

Let $X$ be the random variable where $X=0,500,2000$ and 3000

$\begin{array}{|l|l|l|l|l|l|} \hline X & 0 & 500 & 2000 & 3000 \\ \hline P(X) & \frac{9995}{10000} & \frac{3}{10000} & \frac{1}{10000} & \frac{1}{10000} \\ \hline \end{array}$

Hence, expectation is ₹ 0.65 .

Solution

Let $W_1$ and $W_2$ be two bags containing ( $4 W, 5 B)$ and (9 W, 7 B) balls respectively.

Let $E_1$ be the event that the

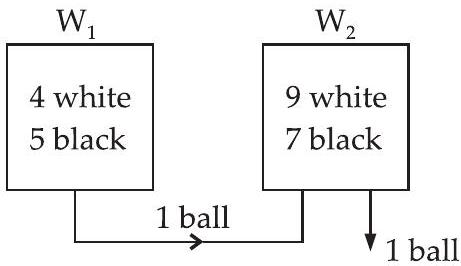
transferred ball from the bag

$W_1$ to $W_2$ is white and $E_2$ the event that the transferred ball is black.

And $E$ be the event that the ball drawn from the second bag is white.

$ \begin{aligned} \therefore P(E / E_1) & =\frac{10}{17}, \quad P(E / E_2)=\frac{9}{17} \\ P(E_1) & =\frac{4}{9} \text{ and } P(E_2)=\frac{5}{9} \\ \therefore \quad P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\frac{4}{9} \times \frac{10}{17}+\frac{5}{9} \times \frac{9}{17}=\frac{40}{153}+\frac{45}{153}=\frac{85}{153}=\frac{5}{9} \end{aligned} $

Hence, the required probability is $\frac{5}{9}$.

Solution

Given that $bag I={3 B, 2 W}$ and $\quad$ bag II $={2 B, 4 W}$

Let $E_1=$ The event that bag I is selected

$ E_2=\text{ The event that bag II is selected } $

and $E=$ The event that a black ball is selected

$ \begin{aligned} \therefore \quad P(E_1) & =\frac{1}{2}, P(E_2)=\frac{1}{2}, P(E _{/} E_1)=\frac{3}{5} \text{ and } P(E_2 E_2)=\frac{1}{3} \\ P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\frac{1}{2} \times \frac{3}{5}+\frac{1}{2} \times \frac{1}{3}=\frac{3}{10}+\frac{1}{6}=\frac{9+5}{30}=\frac{14}{30}=\frac{7}{15} \end{aligned} $

Hence, the required probability is $\frac{7}{15}$.

Solution

Given that the box has 5 blue and 4 red balls.

Let $E_1$ be the event that first ball drawn is blue $E_2$ be the event that first ball drawn is red

and $E$ is the event that second ball drawn is blue.

$ \begin{aligned} \therefore \quad P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\frac{5}{9} \times \frac{4}{8}+\frac{4}{9} \times \frac{5}{8}=\frac{20}{72}+\frac{20}{72}=\frac{40}{72}=\frac{5}{9} \end{aligned} $

Hence, the required probability is $\frac{5}{9}$.

Solution

Let $E_1, E_2, E_3$ and $E_4$ be the events that first, second, third and fourth card is King respectively.

$\therefore P(E_1 \cap E_2 \cap E_3 \cap E_4)$

$=P(E_1) \cdot P(E_2 / E_1) \cdot P[\frac{E_3}{(E_1 \cap E_2)}] \cdot P[\frac{E_4}{(E_1 \cap E_2 \cap E_3 \cap E_4)}]$

$=\frac{4}{52} \times \frac{3}{51} \times \frac{2}{50} \times \frac{1}{49}=\frac{24}{52 \cdot 51 \cdot 50 \cdot 49}=\frac{1}{13 \cdot 17 \cdot 25 \cdot 49}=\frac{1}{27075}$

Hence, the required probability is $\frac{1}{27075}$.

Solution

Here, $p=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2} \Rightarrow q=1-\frac{1}{2}=\frac{1}{2}$ and $n=5$

$ \begin{aligned} \therefore \quad P(x & =r)={ }^{n} C_r p^{r} q^{n-r} \\ & ={ }^{5} C_3(\frac{1}{2})^{3}(\frac{1}{2})^{5-3}=\frac{5 !}{3 ! 2 !} \cdot(\frac{1}{2})^{3} \cdot(\frac{1}{2})^{2}=10 \cdot \frac{1}{8} \cdot \frac{1}{4}=\frac{5}{16} \end{aligned} $

Hence, the required probability is $\frac{5}{16}$.

Solution

Here, $n=10, p=\frac{1}{2}, q=-\frac{1}{2}=\frac{1}{2}$

$ \begin{aligned} & P(X \geq 8)=P(x=8)+P(x=9)+P(x=10) \\ & ={ }^{10} C_8(\frac{1}{2})^{8}(\frac{1}{2})^{10-8}+{ }^{10} C_9(\frac{1}{2})^{9}(\frac{1}{2})^{10-9}+{ }^{10} C _{10}(\frac{1}{2})^{10}(\frac{1}{2})^{0} \\ & =\frac{10 !}{8 ! 2 !} \cdot(\frac{1}{2})^{8} \cdot(\frac{1}{2})^{2}+\frac{10 !}{9 ! 1 !}(\frac{1}{2})^{9}(\frac{1}{2})+(\frac{1}{2})^{10} \\ & =45 \cdot(\frac{1}{2})^{10}+10 \cdot(\frac{1}{2})^{10}+(\frac{1}{2})^{10}=(\frac{1}{2})^{10} \cdot(45+10+1) \\ & =56(\frac{1}{2})^{10}=56 \times \frac{1}{1024}=\frac{7}{128} \end{aligned} $

Hence, the required probability is $\frac{7}{128}$.

Solution

Here $n=7, \quad p=0.25=\frac{25}{100}=\frac{1}{4} \quad$ and $q=1-\frac{1}{4}=\frac{3}{4}$

$ \begin{aligned} P(X \geq 2) & =1-[P(X=0)+P(X=1)] \\ & =1-[{ }^{7} C_0(\frac{1}{4})^{0}(\frac{3}{4})^{7}+{ }^{7} C_1(\frac{1}{4})^{1}(\frac{3}{4})^{6}] \\ & =1-[(\frac{3}{4})^{7}+\frac{7}{4}(\frac{3}{4})^{6}]=1-(\frac{3}{4})^{6}(\frac{3}{4}+\frac{7}{4}) \\ & =1-(\frac{3}{4})^{6}(\frac{10}{4})=1-\frac{729}{4096} \times \frac{10}{4}=1-\frac{7290}{16384} \\ & =\frac{16384-7290}{16384}=\frac{9094}{16384}=\frac{4547}{8192} \end{aligned} $

Hence, the required probability is $\frac{4547}{8192}$.

Solution

Probability of defective watch out of 100 watches $=\frac{10}{100}=\frac{1}{10}$.

Here, $n=8, p=\frac{1}{10}$ and $q=1-\frac{1}{10}=\frac{9}{10}$ and $r \geq 1$

$P(X \geq 1)=1-P(x=0)=1-{ }^{8} C_0(\frac{1}{10})^{0}(\frac{9}{10})^{8-0}=1-(\frac{9}{10})^{8}$

Hence, the required probability is $1-(\frac{9}{10})^{8}$.

Solution

Here, we have

$\begin{array}{|l|l|l|l|l|l|} \hline x & 0 & 1 & 2 & 3 & 4 \\ \hline y & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\ \hline \end{array}$

$=E(X^{2})-[E(X)]^{2}$ |

where $E(X)=\sum _{i=1}^{n} x_i p_i$ and $E(X^{2})=\sum _{i=1}^{n} p_i x_i^{2}$

$\therefore \quad E(X)=0 \times 0.1+1 \times 0.25+2 \times 0.3+3 \times 0.2+4 \times 0.15$

$=0+0.25+0.6+0.6+0.6=2.05$

$E(X^{2})=0 \times 0.1+1 \times 0.25+4 \times 0.3+9 \times 0.2+16 \times 0.15$

$=0+0.25+1.2+1.8+2.40=5.65$

(i) $V(\frac{X}{2})=\frac{1}{4} V(X)=\frac{1}{4}[5.65-(2.05)^{2}]=\frac{1}{4}[5.65-4.2025]$

$=\frac{1}{4} \times 1.4475=0.361875$

$[\because V(\frac{X}{2})=\frac{1}{4} V(X)]$

(ii) $\quad Var(X)=1.4475$

Solution

(i) We know that $P(0)+P(1)+P(2)+P(3)=1$

$ \begin{matrix} \Rightarrow k+\frac{k}{2}+\frac{k}{4}+\frac{k}{8} =1 \\ \Rightarrow \quad \frac{8 k+4 k+2 k+k}{8} =1 \Rightarrow 15 k=8 \\ \therefore \quad k =\frac{1}{15} \end{matrix} $

(ii)

$ \begin{aligned} P(X \leq 2) & =P(X=0)+P(X=1)+P(X=2) \\ & =k+\frac{k}{2}+\frac{k}{4}=\frac{7 k}{4}=\frac{7}{4} \times \frac{8}{15}=\frac{14}{15} \end{aligned} $

and $P(X>2)=P(X=3)=\frac{k}{8}=\frac{1}{8} \times \frac{8}{15}=\frac{1}{15}$

(iii) $P(X \leq 2)+P(X>2)=\frac{14}{15}+\frac{1}{15}=\frac{14+1}{15}=\frac{15}{15}=1$.

Solution

We know that: Standard deviation (S.D.) $=\sqrt{\text{ Variance }}$

$ \begin{aligned} & \therefore \quad Var(X)=E(X^{2})-[E(X)]^{2} \\ & E(X)=2 \times 0.2+3 \times 0.5+4 \times 0.3=0.4+1.5+1.2=3.1 \\ & E(X^{2})=4 \times 0.2+9 \times 0.5+16 \times 0.3=0.8+4.5+4.8=10.1 \\ & V(X)=10.1-(3.1)^{2}=10.1-9.61=0.49 \\ & \therefore \quad \text{ S.D. }=\sqrt{Var(X)}=\sqrt{0.49}=0.7 \end{aligned} $

Solution

Here, random variable $X=0,1,2$

$ \begin{aligned} P(4) & =\frac{1}{10}, P(\overline{4})=1-\frac{1}{10}=\frac{9}{10} \\ P(X=0) & =P(\overline{4}) \cdot P(\overline{4})=\frac{9}{10} \times \frac{9}{10}=\frac{81}{100} \\ P(X=1) & =P(\overline{4}) \cdot P(4)+P(4) \cdot P(\overline{4})=\frac{9}{10} \times \frac{1}{10}+\frac{1}{10} \times \frac{9}{10}=\frac{18}{100} \end{aligned} $

$P(X=2)=P(4) \cdot P(4)=\frac{1}{10} \times \frac{1}{10}=\frac{1}{100}$

$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \\ \hline P(X) & \frac{81}{100} & \frac{18}{100} & \frac{1}{100} \\ \hline \end{array}$

We know that $V(X)=E(X^{2})-[E(X)]^{2}$

$ \begin{aligned} E(X) & =0 \times \frac{81}{100}+1 \times \frac{18}{100}+\frac{2}{100}=\frac{20}{100}=\frac{1}{5} \\ E(X^{2}) & =0 \times \frac{81}{100}+1 \times \frac{18}{100}+4 \times \frac{1}{100}=\frac{22}{100}=\frac{11}{50} \\ \therefore \quad Var(X) & =\frac{11}{50}-(\frac{1}{5})^{2}=\frac{11}{50}-\frac{1}{25}=\frac{9}{50}=0.18 \end{aligned} $

Hence, the required variance $=0.18$.

Solution

Here, we have $X=0,1,2,3 \quad[\because$ die is thrown 3 times] and $p=\frac{1}{6}, q=\frac{5}{6}$

$\therefore P(X=0)=P(not 2) \cdot P(not 2) \cdot P(not 2)=\frac{5}{6} \cdot \frac{5}{6} \cdot \frac{5}{6}=\frac{125}{216}$

$P(X=1)=P(2) \cdot P(not 2) \cdot P(not 2)+P(not 2) \cdot P(2) \cdot P(not 2)$

$+P($ not 2$) . P(not 2) \cdot P(2)$

$=\frac{1}{6} \cdot \frac{5}{6} \cdot \frac{5}{6}+\frac{5}{6} \cdot \frac{1}{6} \cdot \frac{5}{6}+\frac{5}{6} \cdot \frac{5}{6} \cdot \frac{1}{6}=\frac{25}{216}+\frac{25}{216}+\frac{25}{216}=\frac{75}{216}$

$P(X=2)=P(2) \cdot P(2) \cdot P(not 2)+P(2) \cdot P(not 2) \cdot P(2)$

$+P($ not 2$) \cdot P(2) \cdot P(2)$

$=\frac{1}{6} \cdot \frac{1}{6} \cdot \frac{5}{6}+\frac{1}{6} \cdot \frac{5}{6} \cdot \frac{1}{6}+\frac{5}{6} \cdot \frac{1}{6} \cdot \frac{1}{6}=\frac{5}{216}+\frac{5}{216}+\frac{5}{216}=\frac{15}{216}$

$P(X=3)=P(2) \cdot P(2) \cdot P(2)=\frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6}=\frac{1}{216}$

Now $E(X)=\sum _{i=1}^{n} p_i x_i$

$ \begin{aligned} & i=1 \\ & 0 \times \frac{125}{216}+1 \times \frac{75}{216}+2 \times \frac{15}{216}+3 \times \frac{1}{216} \\ = & 0+\frac{75}{216}+\frac{30}{216}+\frac{3}{216}=\frac{75+30+3}{216}=\frac{108}{216}=\frac{1}{2} \end{aligned} $

Hence, the required expectation is $\frac{1}{2}$.

Solution

Given that: for the first die, $P(6)=\frac{1}{2}$ and $P(\overline{6})=1-\frac{1}{2}=\frac{1}{2}$

$\Rightarrow P(1)+P(2)+P(3)+P(4)+P(5)=\frac{1}{2}$

But $P(1)=P(2)=P(3)=P(4)=P(5)$

$\therefore 5 . P(1)=\frac{1}{2} \Rightarrow P(1)=\frac{1}{10}$ and $P(\overline{1})=1-\frac{1}{10}=\frac{9}{10}$

For the second die, $P(1)=\frac{2}{5}$ and $P(\overline{1})=1-\frac{2}{5}=\frac{3}{5}$

Let $X$ be the number of one’s seen

$ \begin{aligned} \therefore X=0,1,2 \\ \Rightarrow \quad \begin{aligned} P(X=0) =P(\overline{1}) \cdot P _{II}(\overline{1})=\frac{9}{10} \cdot \frac{3}{5}=\frac{27}{50}=0.54 \\ P(X=1) =P(\overline{1}) \cdot P_I(1)+P(1) \cdot P _{(\overline{1})} \\ =\frac{9}{10} \cdot \frac{2}{5}+\frac{1}{10} \cdot \frac{3}{5}=\frac{18+3}{50}=\frac{21}{50}=0.42 \\ P(X=2) =\underset{I \hspace{2mm} II}{P(1) \cdot P(1)}=\frac{1}{10} \cdot \frac{2}{5}=\frac{2}{50}=0.04 \end{aligned} \end{aligned} $

Hence, the required probability distribution is

$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \\ \hline P(X) & 0.54 & 0.42 & 0.04 \\ \hline \end{array}$

Solution

First probability distribution is given by

$\begin{array}{|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 \\ \hline P(X) & \frac{1}{5} & \frac{2}{5} & \frac{1}{5} & \frac{1}{5} \\ \hline \end{array}$

We know that, $E(X)=\sum _{i=1}^{n} P_i X_i$

$\Rightarrow E(X)=0 \cdot \frac{1}{5}+1 \cdot \frac{2}{5}+2 \cdot \frac{1}{5}+3 \cdot \frac{1}{5}=0+\frac{2}{5}+\frac{2}{5}+\frac{3}{5}=\frac{7}{5}$

For the second probability distribution,

$\begin{array}{|l|l|l|l|l|} \hline (Y) & 0 & 1 & 2 & 3 \\ \hline P(Y) & \frac{1}{5} & \frac{3}{10} & \frac{2}{5} & \frac{1}{10} \\ \hline \end{array}$

$ \begin{aligned} E(Y^{2}) & =0 \cdot \frac{1}{5}+1 \cdot \frac{3}{10}+4 \cdot \frac{2}{5}+9 \cdot \frac{1}{10} \\ & =0+\frac{3}{10}+\frac{8}{5}+\frac{9}{10}=\frac{28}{10}=\frac{14}{5} \end{aligned} $

Now $E(Y^{2})=\frac{14}{5}$ and $2 E(X)=2 \cdot \frac{7}{5}=\frac{14}{5}$

Hence, $E(Y^{2})=2 E(X)$.

Solution

Let $X$ be the random variable denoting a bulb to be defective.

Here, $n=10, p=\frac{1}{50}, q=1-\frac{1}{50}=\frac{49}{50}$

We know that $P(X=r)={ }^{n} C_r p^{r} q^{n-r}$

(i) None of the bulbs is defective, i.e., $r=0$

$ P(x=0)={ }^{10} C_0(\frac{1}{50})^{0}(\frac{49}{50})^{10-0}=(\frac{49}{50})^{10} $

(ii) Exactly two bulbs are defective

$ \begin{aligned} \therefore \quad P(x=2) & ={ }^{10} C_2(\frac{1}{50})^{2}(\frac{49}{50})^{10-2} \\ & =45 \cdot \frac{(49)^{8}}{(50)^{10}}=45 \times(\frac{1}{50})^{10} \times(49)^{8} \end{aligned} $

(iii) More than 8 bulbs work properly

We can say that less than 2 bulbs are defective

$ P(x<2)=P(x=0)+P(x=1) $

$={ }^{10} C_0(\frac{1}{50})^{0}(\frac{49}{50})^{10}+{ }^{10} C_1(\frac{1}{50})^{1}(\frac{49}{50})^{9}=(\frac{49}{50})^{10}+\frac{1}{5}(\frac{49}{50})^{9}$

$ =(\frac{49}{50})^{9}(\frac{49}{50}+\frac{1}{5})=(\frac{49}{50})^{9}(\frac{59}{50})=\frac{59(49)^{9}}{(50)^{10}} . $

Solution

Let $E_1=$ Event that the coin is fair

$ E_2=\text{ Event that the coin is 2-headed } $

and $H=$ Event that the tossed coin gets head.

$ P(E_1)=\frac{1}{2}, \quad P(E_2)=\frac{1}{2}, \quad P(H / E_1)=\frac{1}{2}, \quad P(H / E_2)=1 $

$\therefore$ Using Bayes’ Theorem, we get

$ \begin{aligned} P(E_1 / H) & =\frac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\frac{\frac{1}{2} \cdot \frac{1}{2}}{\frac{1}{2} \cdot \frac{1}{2}+\frac{1}{2} \cdot 1}=\frac{\frac{1}{4}}{\frac{1}{4}+\frac{1}{2}}=\frac{\frac{1}{3}}{\frac{3}{4}}=\frac{1}{3} \end{aligned} $

Hence the required probability is $\frac{1}{3}$.

Solution

Let $E_1=$ The event that a person selected is of blood group $O$ $E_2=$ The event that the person selected is of other group and $H=$ The event that selected person is left handed

$ \begin{matrix} \therefore \quad P(E_1) & =0.30 \text{ and } & P(E_2)=0.70 \\ P(H / E_1) & =0.06 & P(H / E_2)=0.10 \end{matrix} $

So, from Bayes’ Theorem

$ \begin{aligned} & \quad P(\frac{E_1}{H})=\frac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\frac{0.30 \times 0.06}{0.30 \times 0.06+0.70 \times 0.10}=\frac{0.018}{0.018+0.070}=\frac{0.018}{0.088}=\frac{9}{44} \\ & \text{ Hence, the required probability is } \frac{9}{44} . \end{aligned} $

Solution

Given that: $S={1,2,3, \ldots, n}$

$ \therefore \quad P(r \leq p / s \leq p)=\frac{P(P \cap S)}{P(S)}=\frac{p-1}{n} \times \frac{n}{n-1}=\frac{p-1}{n-1} $

Hence, the required probability is $\frac{p-1}{n-1}$.

Solution

Let $X$ be the random variable scores when a die is thrown twice.

and

$ \begin{aligned} X & =1,2,3,4,5,6 \\ S & =\{(1,1),(1,2),(2,1),(2,2),(1,3),(2,3),(3,1),(3,2),(3,3),(3,4),(3,5),..,(6,6)\} \end{aligned} $

So, $\quad P(X=1)=\frac{1}{6} \cdot \frac{1}{6}=\frac{1}{36}$

$ \begin{aligned} & P(X=2)=\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}=\frac{3}{36} \\ & P(X=3)=\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}+\frac{1}{6} \cdot \frac{1}{6}=\frac{5}{36} \end{aligned} $

Similarly

$ P(X=4)=\frac{7}{36} ; P(X=5)=\frac{9}{36} \text{ and } P(X=6)=\frac{11}{36} $

So, the required distribution is

$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline P(X) & \frac{1}{36} & \frac{3}{36} & \frac{5}{36} & \frac{7}{36} & \frac{9}{36} &\frac{11}{36} \\ \hline \end{array}$

Now, the mean $E(X)=\sum _{i=1}^{n} x_i p_i$

$ \begin{aligned} & =1 \times \frac{1}{36}+2 \times \frac{3}{36}+3 \times \frac{5}{36}+4 \times \frac{7}{36}+5 \times \frac{9}{36}+6 \times \frac{11}{36} \\ & =\frac{1}{36}+\frac{6}{36}+\frac{15}{36}+\frac{28}{36}+\frac{45}{36}+\frac{66}{36}=\frac{161}{36} \end{aligned} $

Hence, the required mean $=\frac{161}{36}$.

Solution

Given that: $\quad X=0,1,2$ and $P(X)$ at $X=0$ and 1 is $p$. Let $P(X)$ at $X=2$ is $x$

$\Rightarrow \quad p+p+x=1 \quad \Rightarrow \quad x=1-2 p$

Now we have the following distributions.

$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \\ \hline P(X) & p & p & 1-2p \\ \hline \end{array}$

$\therefore \quad E(X)=0 . p+1 . p+2(1-2 p)=p+2-4 p=2-3 p$

and $\quad E(X^{2})=0 . p+1 . p+4(1-2 p)=p+4-8 p=4-7 p$

Given that: $\quad E(X^{2})=E(X)$

$\therefore \quad 4-7 p=2-3 p \Rightarrow 4 p=2 \Rightarrow p=\frac{1}{2}$

Hence, the required value of $p$ is $\frac{1}{2}$.

Solution

We know that:

$ \begin{aligned} & \text{ Variance }(X)=E(X^{2})-[E(X)]^{2} \\ & E(X)=\sum _{i=1}^{n} p_i x_i \\ &=0 \times \frac{1}{6}+1 \times \frac{5}{18}+2 \times \frac{2}{9}+3 \times \frac{1}{6}+4 \times \frac{1}{9}+5 \times \frac{1}{18} \\ &=0+\frac{5}{18}+\frac{4}{9}+\frac{3}{6}+\frac{4}{9}+\frac{5}{18}=\frac{5+8+9+8+5}{18}=\frac{35}{18} \\ & E(X^{2})=0 \times \frac{1}{6}+1 \times \frac{5}{18}+4 \times \frac{2}{9}+9 \times \frac{1}{6}+16 \times \frac{1}{9}+25 \times \frac{1}{18} \\ &=\frac{5}{18}+\frac{8}{9}+\frac{9}{6}+\frac{16}{9}+\frac{25}{18}=\frac{5+16+27+32+25}{18}=\frac{105}{18} \\ & \therefore \text{ Var }(X)=\frac{105}{18}-\frac{35}{18} \times \frac{35}{18}=\frac{1890-1225}{324}=\frac{665}{324} \\ & \text{ Hence, the required variance is } \frac{665}{324} . \end{aligned} $

Solution

Let $A_1$ be the event of getting a total of 6

$ ={(2,4),(4,2),(1,5),(5,1),(3,3)} $

and $B_1$ be the event of getting a total of 7

$ ={(2,5),(5,2),(1,6),(6,1),(3,4),(4,3)} $

Let $P(A_1)$ is the probability, if $A$ wins in a throw $=\frac{5}{36}$

and $P(B_1)$ is the probability, if $B$ wins in a throw $=\frac{1}{6}$

$\therefore$ The required probability of winning $A$ in his third throw

$ =P(\overline{A}_1) \cdot P(\overline{B}_1) \cdot P(A_1)=\frac{31}{36} \cdot \frac{5}{6} \cdot \frac{5}{36}=\frac{775}{7776} . $

Solution

Given that:

$A=\{(x, y): x+y=11\} \text{ and } B=\{(x, y): x \neq 5\}$

$\therefore \quad A=\{(5,6),(6,5)\},$

$B=\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),$ $(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(6,1),(6,2),$ $ (6,3),(6,4),(6,5),(6,6)\}$

$ \begin{aligned} & \Rightarrow n(A)=2, n(B)=30 \text{ and } n(A \cap B)=1 \\ & \therefore \quad P(A)=\frac{2}{36}=\frac{1}{18} \text{ and } P(B)=\frac{30}{36}=\frac{5}{6} \\ & \Rightarrow \quad P(A) \cdot P(B)=\frac{1}{18} \cdot \frac{5}{6}=\frac{5}{108} \text{ and } P(A \cap B)=\frac{1}{36} \end{aligned} $

Since $P(A).P(B) \neq P(P \cap B)$

Hence, A and B are not independent.

Solution

Let $A$ be the event having $m$ white and $n$ black balls

$ \begin{aligned} & E_1={\text{ first ball drawn of white colour }} \\ & E_2={\text{ first ball drawn of black colour }} \end{aligned} $

$ \begin{aligned} & E_3={\text{ second ball drawn of white colour }} \\ & \therefore \quad P(E_1)=\frac{m}{m+n} \text{ and } P(E_2)=\frac{n}{m+n} \\ & P(E_3 / E_1)=\frac{m+k}{m+n+k} \text{ and } P(E_3 / E_2)=\frac{m}{m+n+k} \\ & \text{ Now } P(E_3)=P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2) \\ &=\frac{m}{m+n} \times \frac{m+k}{m+n+k}+\frac{n}{m+n} \times \frac{m}{m+n+k} \\ &=\frac{m}{m+n+k}[\frac{m+k}{m+n}+\frac{n}{m+n}] \\ &=\frac{m}{m+n+k}[\frac{m+n+k}{m+n}]=\frac{m}{m+n} \end{aligned} $

Hence, the probability of drawing a white ball does not depend upon $k$.

Solution

Given that:

Bag I: 3 red balls and no white ball

Bag II: 2 red balls and 1 white ball

Bag III: no red ball and 3 white balls

Let $E_1, E_2$ and $E_3$ be the events of choosing Bag I, Bag II and Bag III respectively and a ball is drawn from it.

$\therefore P(E_1)=\frac{1}{6}, P(E_2)=\frac{2}{6}$ and $P(E_3)=\frac{3}{6}$

(i) Let $E$ be the event that red ball is selected

$ \begin{aligned} \therefore P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2)+P(E_3) \cdot P(E / E_3) \\ & =\frac{1}{6} \cdot \frac{3}{3}+\frac{2}{6} \cdot \frac{2}{3}+\frac{3}{6} \cdot 0=\frac{3}{18}+\frac{4}{18}=\frac{7}{18} \end{aligned} $

(ii) Let $F$ be the event that a white ball is selected

$ \begin{matrix} \therefore P(F) & =1-P(E) & {[P(E)+P(F)=1]} \\ & =1-\frac{7}{18}=\frac{11}{18} & \end{matrix} $

Hence, the required probabilities are $\frac{7}{18}$ and $\frac{11}{18}$.

Solution

Referring to Exercise Q.41, we will use here Bayes’ Theorem

$ \begin{aligned} & \text{ (i) } \begin{aligned} P(E_2 / F) & =\frac{P(E_2) \cdot P(F / E_2)}{P(E_1) \cdot P(F / E_1)+P(E_2) \cdot P(F / E_2)+P(E_3) \cdot P(F / E_3)} \\ & =\frac{\frac{2}{6} \cdot \frac{1}{3}}{\frac{1}{6} \cdot 0+\frac{2}{6} \cdot \frac{1}{3}+\frac{3}{6} \cdot 1}=\frac{\frac{2}{18}}{\frac{2}{18}+\frac{3}{6}}=\frac{2}{11} \\ \text{ (ii) } P(E_3 / F) & =\frac{P(E_3) \cdot P(F / E_3)}{P(E_1) \cdot P(F / E_1)+P(E_2) \cdot P(F / E_2)+P(E_3) \cdot P(F / E_3)} \\ & =\frac{\frac{3}{6} \cdot 1}{\frac{1}{6} \cdot 0+\frac{2}{6} \cdot \frac{1}{3}+\frac{3}{6} \cdot 1}=\frac{\frac{3}{6}}{\frac{2}{18}+\frac{3}{6}}=\frac{3}{6} \times \frac{18}{11}=\frac{9}{11} \end{aligned} \\ & \text{ Hence, the required probabilities are } \frac{2}{11} \text{ and } \frac{9}{11} . \end{aligned} $

Solution

Given that $A_1: A_2: A_3=4: 4: 2$

$\therefore P(A_1)=\frac{4}{10}, P(A_2)=\frac{4}{10}$ and $P(A_3)=\frac{2}{10}$

where $A_1, A_2$ and $A_3$ are the three types of seeds.

Let $E$ be the event that a seed germinates and $\overline{E}$ be the event that a seed does not germinate

$\therefore P(\frac{E}{A_1})=\frac{45}{100}, P(\frac{E}{A_2})=\frac{60}{100}$ and $P(\frac{E}{A_3})=\frac{35}{100}$

and $P(\frac{\overline{E}}{A_1})=\frac{55}{100}, P(\frac{\overline{E}}{A_2})=\frac{40}{100}$ and $P(\frac{\overline{E}}{A_3})=\frac{65}{100}$ (i)

$ \begin{aligned} P(E) & =P(A_1) \cdot P(\frac{E}{A_1})+P(A_2) \cdot P(\frac{E}{A_2})+P(A_3) \cdot P(\frac{E}{A_3}) \\ & =\frac{4}{10} \cdot \frac{45}{100}+\frac{4}{10} \cdot \frac{60}{100}+\frac{2}{10} \cdot \frac{35}{100} \\ & =\frac{180}{1000}+\frac{240}{1000}+\frac{70}{1000}=\frac{490}{1000}=0.49 \end{aligned} $

(ii) $P(\overline{E} / A_3)=1-P(E / A_3)=1-\frac{35}{100}=\frac{65}{100}=0.65$

(iii) Using Bayes’ Theorem, we get

$ \begin{aligned} & P(A_2 / \overline{E})=\frac{P(A_2) \cdot P(\overline{E} / A_2)}{P(A_1) \cdot P(\overline{E} / A_1)+P(A_2) \cdot P(\overline{E} / A_2)+P(A_3) \cdot P(\overline{E} / A_3)} \\ &= \frac{\frac{4}{10} \cdot \frac{40}{100}}{\frac{4}{10} \cdot \frac{55}{100}+\frac{4}{10} \cdot \frac{40}{100}+\frac{2}{10} \cdot \frac{65}{100}} \\ &=\frac{\frac{160}{1000}}{\frac{220}{1000}+\frac{160}{1000}+\frac{130}{1000}}=\frac{160}{220+160+130}=\frac{160}{510}=\frac{16}{51}=0.314 \end{aligned} $

Hence, the required probability is $\frac{16}{51}$ or 0.314 .

Solution

Let $E_1$ : The event that the letter comes from TATANAGAR and $E_2$ : The event that the letter comes from CALCUTTA Also $E_3$ : The event that on the letter, two consecutive letters TA are visible

$\therefore P(E_1)=\frac{1}{2}$ and $P(E_2)=\frac{1}{2}$ and $P(\frac{E_3}{E_1})=\frac{2}{8}$ and $P(\frac{E_3}{E_2})=\frac{1}{7}$

$[\because$ For TATA NAGAR, the two consecutive letters visible are TA, AT, TA, AN, NA, AG, GA, AR] $\therefore P(E_3 / E_1)=\frac{2}{8}$ and [For CALCUTTA, the two consecutive letters visible are $CA, AL, LC, CU, UT, TT$ and TA] So, $P(E_3 / E_2)=\frac{1}{7}$ Now using Bayes’ Theorem, we have

$ P(E_1 / E_3)=\frac{P(E_1) \cdot P(E_3 / E_1)}{P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2)} $

$ =\frac{\frac{1}{2} \cdot \frac{2}{8}}{\frac{1}{2} \cdot \frac{2}{8}+\frac{1}{2} \cdot \frac{1}{7}}=\frac{\frac{1}{8}}{\frac{1}{8}+\frac{1}{14}}=\frac{\frac{1}{8}}{\frac{7+4}{56}}=\frac{7}{11} $

Hence, the required probability is $\frac{7}{11}$.

Solution

Let $E_1$ be the event of selecting Bag I and $E_2$ be the event of selecting Bag II

Let $E_3$ be the event that black ball is selected

$ \begin{aligned} \therefore \quad P(E_1) & =\frac{2}{6}=\frac{1}{3} \text{ and } P(E_2)=1-\frac{1}{3}=\frac{2}{3} \\ P(E_3 / E_1) & =\frac{3}{7} \text{ and } P(E_3 / E_2)=\frac{4}{7} \\ \therefore \quad P(E_3) & =P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2) \\ & =\frac{1}{3} \cdot \frac{3}{7}+\frac{2}{3} \cdot \frac{4}{7}=\frac{3+8}{21}=\frac{11}{21} \end{aligned} $

Hence, the required probability is $\frac{11}{21}$.

Solution

We have 3 urns:

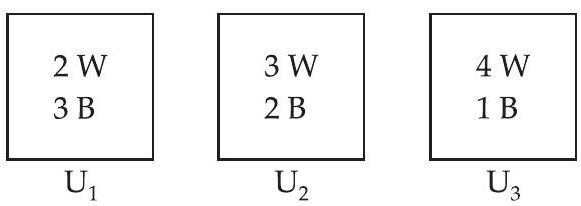
$\therefore$ Probabilities of choosing either of the urns are

$ P(U_1)=P(U_2)=P(U_3)=\frac{1}{3} $

Let $H$ be the event of drawing white ball from the chosen urn.

$ \begin{aligned} & \therefore P(H / U_1)=\frac{2}{5}, P(H / U_2)=\frac{3}{5} \text{ and } P(H / U_3)=\frac{4}{5} \\ & \therefore P(U_2 / H)=\frac{P(U_2) \cdot P(H / U_2)}{P(U_1) \cdot P(H / U_1)+P(U_2) \cdot P(H / U_2)+P(U_3) \cdot P(H / U_3)} \\ & \quad=\frac{\frac{1}{3} \cdot \frac{3}{5}}{\frac{1}{3} \cdot \frac{2}{5}+\frac{1}{3} \cdot \frac{3}{5}+\frac{1}{3} \cdot \frac{4}{5}}=\frac{\frac{3}{5}}{\frac{2}{5}+\frac{3}{5}+\frac{4}{5}}=\frac{3}{9}=\frac{1}{3} \end{aligned} $

Hence, the required probability is $\frac{1}{3}$.

Solution

Let $E_1$ : Event that a person has TB

$ E_2 \text{ : Event that a person does not have TB } $

and $H$ : Event that the person is diagnosed to have TB.

$ \begin{aligned} & \therefore \quad P(E_1)=\frac{1}{1000}=0.001, P(E_2)=1-\frac{1}{1000}=\frac{999}{1000}=0.999 \\ & P(H / E_1)=0.99, P(H / E_2)=0.001 \\ & \therefore P(E_1 / H)=\frac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\frac{0.001 \times 0.99}{0.001 \times 0.99+0.999 \times 0.001}=\frac{0.99}{0.99+0.999} \\ & =\frac{0.990}{0.990+0.999}=\frac{990}{1989}=\frac{110}{221} \end{aligned} $

Hence, the required probability is $\frac{110}{221}$.

Solution

Let $E_1$ : The event that the item is manufactured on machine A

$E_2$ : The event that the item is manufactured on machine $B$

$E_3$ : The event that the item is manufactured on machine C

Let $H$ be the event that the selected item is defective.

$\therefore$ Using Bayes’ Theorem,

$ \begin{aligned} & P(E_1)=\frac{50}{100}, P(E_2)=\frac{30}{100}, P(E_3)=\frac{20}{100} \\ & P(H / E_1)=\frac{2}{100}, P(H / E_2)=\frac{2}{100} \text{ and } P(H / E_3)=\frac{3}{100} \\ & \therefore P(E_1 / H)=\frac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)+P(E_3) \cdot P(H / E_3)} \\ & =\frac{\frac{50}{100} \times \frac{2}{100}}{\frac{50}{100} \times \frac{2}{100}+\frac{30}{100} \times \frac{2}{100}+\frac{20}{100} \times \frac{3}{100}} \\ & =\frac{100}{100+60+60}=\frac{100}{220}=\frac{10}{22}=\frac{5}{11} \end{aligned} $

Solution

(i) Here, $P(X=x)=k(x+1)$ for $x=1,2,3,4$

So, $P(X=1)=k(1+1)=2 k ; P(X=2)=k(2+1)=3 k$

$ P(X=3)=k(3+1)=4 k ; P(X=4)=k(4+1)=5 k $

Also, $P(X=x)=2 k x$ for $x=5,6,7$

$ \begin{aligned} & P(X=5)=2(5) k=10 k ; P(X=6)=2(6) k=12 k \\ & P(X=7)=2(7) k=14 k \end{aligned} $

and for otherwise it is 0 .

$\therefore$ The probability distribution is given by

$\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \text{otherwise} \\ \hline P(X) & 2k & 3k & 4k & 5k & 10k & 12k & 14k & 0 \\ \hline \end{array}$

$ \begin{aligned} & \text{ We know that } \sum _{i=1}^{n} P(X_i)=1 \\ & \text{ So, } 2 k+3 k+4 k+5 k+10 k+12 k+14 k=1 \\ & \Rightarrow \quad 50 k=1 \Rightarrow k=\frac{1}{50} \\ & \text{ Hence, the value of } k \text{ is } \frac{1}{50} \end{aligned} $

(ii) Now the probability distribution is

$\begin{array}{|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline P(X) & \frac{2}{50} & \frac{3}{50} & \frac{4}{50} & \frac{5}{50} & \frac{10}{50} & \frac{12}{50} &\frac{14}{50} \\ \hline \end{array}$

$ \begin{aligned} E(X)=1 \times \frac{2}{50}+2 \times \frac{3}{50}+3 \times \frac{4}{50}+4 \times \frac{5}{50}+5 \times \frac{10}{50}+ & 6 \times \frac{12}{50} \\ & +7 \times \frac{14}{50} \end{aligned} $

$ =\frac{2}{50}+\frac{6}{50}+\frac{12}{50}+\frac{20}{50}+\frac{50}{50}+\frac{72}{50}+\frac{98}{50}=\frac{260}{50}=\frac{26}{5}=5.2 $

(iii) We know that Standard deviation (SD) $=\sqrt{\text{ Variance }}$ Variance $=E(X^{2})-[E(X)]^{2}$

$ \begin{aligned} & \begin{aligned} & E(X^{2})= 1 \times \frac{2}{50}+4 \times \frac{3}{50}+9 \times \frac{4}{50}+16 \times \frac{5}{50}+25 \times \frac{10}{50} \\ &=\frac{2}{50}+\frac{12}{50}+\frac{36}{50}+\frac{80}{50}+\frac{250}{50}+\frac{432}{50}+\frac{686}{50}=\frac{1498}{50} \end{aligned} \\ & \therefore \text{ Variance }(X)=\frac{1498}{50}-(\frac{26}{5})^{2} \\ & =\frac{1498}{50}-\frac{676}{25}=\frac{1498-1352}{50}=\frac{146}{50}=2.92 \\ & \therefore \quad \text{ S.D }=\sqrt{2.92}=1.7 \text{ (approx.) } \end{aligned} $

Solution

(i) We know that: $E(X)=\sum _{i=1}^{n} P_i X_i$

$ \begin{matrix} \therefore & E(X) & =1 \times \frac{1}{2}+2 \times \frac{1}{5}+4 \times \frac{3}{25}+2 A \times \frac{1}{10}+3 A \times \frac{1}{25}+5 A \times \frac{1}{25} \\ & 2.94 & =\frac{1}{2}+\frac{2}{5}+\frac{12}{25}+\frac{A}{5}+\frac{3 A}{25}+\frac{A}{5} \\ \Rightarrow & 2.94 & =0.5+0.4+0.48+\frac{13 A}{25}=1.38+\frac{13 A}{25} \\ \Rightarrow & 2.94 & -1.38=\frac{13 A}{25} \Rightarrow 1.56=\frac{13 A}{25} \\ \Rightarrow \quad & A & =\frac{1.56 \times 25}{13}=0.12 \times 25 \\ & \therefore \quad & A & =3 \end{matrix} $

(ii) Now the distribution becomes

$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 4 & 6 & 9 & 15 \\ \hline P(X) & \frac{1}{2} & \frac{1}{5} & \frac{3}{25} & \frac{1}{10} & \frac{1}{25} & \frac{1}{25} \\ \hline \end{array}$

$E(X^{2})=1 \times \frac{1}{2}+4 \times \frac{1}{5}+16 \times \frac{3}{25}+36 \times \frac{1}{10}+81 \times \frac{1}{25}+225 \times \frac{1}{25}$

$ \begin{aligned} & =\frac{1}{2}+\frac{4}{5}+\frac{48}{25}+\frac{36}{10}+\frac{81}{25}+\frac{225}{25} \\ & =0.5+0.8+1.92+3.6+3.24+9.00=19.06 \end{aligned} $

Variance $(X)=E(X^{2})-[E(X)]^{2}$

$ =19.06-(2.94)^{2}=19.06-8.64=10.42 $

Solution

Given that: $\quad P(X=x)=\begin{cases} k x^{2} & \text{ for } x=1,2,3 \\ 2 k x & \text{ for } x=4,5,6 \\ 0 & \text{ otherwise } \end{cases} .$

$\therefore$ Probability distribution of random variable $X$ is

$\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & \text{otherwise} \\ \hline P(X) & k & 4k & 9k & 8k & 10k & 0 \\ \hline \end{array}$

We know that $\sum _{i=1}^{n} P(X_i)=1$

$\therefore k+4 k+9 k+8 k+10 k+12 k=1 \Rightarrow 44 k=1 \Rightarrow k=\frac{1}{44}$

(i) $E(X)=\sum _{i=1}^{n} P_i X_i=1 \times k+2 \times 4 k+3 \times 9 k+4 \times 8 k+5 \times 10 k+6 \times 12 k$ $=k+8 k+27 k+32 k+50 k+72 k=190 k$ $=190 \times \frac{1}{44}=\frac{95}{22}=4.32$ (approx.)

(ii) $E(3 X^{2})=3[k+4 \times 4 k+9 \times 9 k+16 \times 8 k+25 \times 10 k+36 \times 12 k]$

$=3[k+16 k+81 k+128 k+250 k+432 k]=3[908 k]$

$=3 \times 908 \times \frac{1}{44}=\frac{2724}{44}=61.9$ (approx.)

(iii) $P(X \geq 4)=P(X=4)+P(X=5)+P(X=6)$

$=8 k+10 k+12 k=30 k$

$=30 \times \frac{1}{44}=\frac{15}{22}$.

Solution

Given that $n$ coins are two headed coins and the remaining $(n+1)$ coins are fair.

Let $E_1$ : the event that unfair coin is selected

$E_2$ : the event that the fair coin is selected

$E$ : the event that the toss results in a head

$\therefore \quad P(E_1)=\frac{n}{2 n+1}$ and $P(E_2)=\frac{n+1}{2 n+1}$

$P(E / E_1)=1$ (sure event) and $P(E / E_2)=\frac{1}{2}$

$\therefore \quad P(E)=P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2)$

$=\frac{n}{2 n+1} \cdot 1+\frac{n+1}{2 n+1} \cdot \frac{1}{2}=\frac{1}{2 n+1}(n+\frac{n+1}{2})$

$=\frac{1}{2 n+1}(\frac{2 n+n+1}{2})=\frac{3 n+1}{2(2 n+1)}$

But $\quad P(E)=\frac{31}{42}$ (given)

$ \begin{matrix} \therefore \frac{3 n+1}{2(2 n+1)}=\frac{31}{42} & \Rightarrow & \frac{3 n+1}{2 n+1} & =\frac{31}{21} \\ & \Rightarrow & 63 n+21 & =62 n+31 \\ & \Rightarrow & & n & =10 \end{matrix} $

Hence, the required value of $n$ is 10 .

Solution

Let $X$ be the random variable such that $X=0,1,2$

and $E=$ the event of drawing an ace

and $F=$ the event of drawing non-ace.

$\therefore P(E)=\frac{4}{52}$ and $P(\overline{E})=\frac{48}{52}$

Now $P(X=0)=P(\overline{E}) \cdot P(\overline{E})=\frac{48}{52} \cdot \frac{47}{51}=\frac{188}{221}$

$ \begin{gathered} P(X=1)=P(E) \cdot P(\bar{{}E})+P(\bar{{}E}) \cdot P(E)=\frac{4}{52} \times \frac{48}{51}+\frac{48}{52} \times \frac{4}{51}=\frac{32}{221} \\ P(X=2)=P(E) \cdot P(E)=\frac{4}{52} \cdot \frac{3}{51}=\frac{1}{221} \end{gathered} $

We have Distribution Table:

$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \\ \hline P(X) & \frac{188}{221} & \frac{32}{221} & \frac{1}{221} \\ \hline \end{array}$

Now, Mean $E(X)=0 \times \frac{188}{221}+1 \times \frac{32}{221}+2 \times \frac{1}{221}=\frac{32}{221}+\frac{2}{221}=\frac{34}{221}=\frac{2}{13}$

$ E(X^{2})=0 \times \frac{188}{221}+1 \times \frac{32}{221}+4 \times \frac{1}{221}=\frac{32}{221}+\frac{4}{221}=\frac{36}{221} $

$\therefore \quad$ Variance $=E(X^{2})-[E(X)]^{2}$

$ =\frac{36}{221}-(\frac{2}{13})^{2}=\frac{36}{221} \quad \frac{4}{169}=\frac{468-68}{13 \times 221}=\frac{400}{2873} $

Standard deviation $=\sqrt{\frac{400}{2873}}=0.377$ (approx.)

Solution

Let $E$ be the event of getting even number on tossing a die.

$\therefore P(E)=\frac{3}{6}=\frac{1}{2}$ and $P(\overline{E})=1-\frac{1}{2}=\frac{1}{2}$

Here $X=0,1,2$

$ \begin{gathered} P(X=0)=P(\bar{{}E}) \cdot P(\bar{{}E})=\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4} \\ P(X=1)=P(E) \cdot P(\bar{{}E})+P(\bar{{}E}) \cdot P(E)=\frac{1}{2} \cdot \frac{1}{2}+\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4}+\frac{1}{4}=\frac{2}{4} \\ P(X=2)=P(E) \cdot P(E)=\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4} \end{gathered} $

$\therefore$ Probability distribution table is

$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \\ \hline P(X) & \frac{1}{4} & \frac{2}{4} & \frac{1}{4} \\ \hline \end{array}$

$ \begin{aligned} E(X) & =0 \times \frac{1}{4}+1 \times \frac{2}{4}+2 \times \frac{1}{4}=\frac{2}{4}+\frac{2}{4}=1 \\ E(X^{2}) & =0 \times \frac{1}{4}+1 \times \frac{2}{4}+4 \times \frac{1}{4}=\frac{3}{2} \end{aligned} $

$\therefore$ Variance $(X)=E(X^{2})-[E(X)]^{2}=\frac{3}{2}-1=\frac{1}{2}=0.5$

Solution

Here, sample space $S=\{(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)$, $(1,4),(4,1),(1,5),(5,1),(2,4),(4,2),(2,5),(5,2),(3,4),(4,3)$, $(3,5),(5,3),(5,4),(4,5)\}$

$\therefore n(S)=20$

Let $X$ be the random variable denoting the sum of the numbers on two cards drawn.

$ \therefore \quad X=3,4,5,6,7,8,9 $

So, $\quad P(X=3)=\frac{2}{20}$

$ \begin{aligned} & P(X=4)=\frac{2}{20} \\ & P(X=6)=\frac{4}{20} \\ & P(X=8)=\frac{2}{20} \end{aligned} $

$ \begin{aligned} & P(X=5)=\frac{4}{20} \\ & P(X=7)=\frac{4}{20} \end{aligned} $

$ \begin{matrix} P(X=9)=\frac{2}{20} \\ \therefore \text{ Mean, } E(X)=3 \times \frac{2}{20}+4 \times \frac{2}{20}+5 \times \frac{4}{20}+6 \times \frac{4}{20}+7 \times \frac{4}{20} \\ +8 \times \frac{2}{20}+9 \times \frac{2}{20} \\ =\frac{6}{20}+\frac{8}{20}+\frac{20}{20}+\frac{24}{20}+\frac{28}{20}+\frac{16}{20}+\frac{18}{20}=\frac{120}{20}=6 \\ E(X^{2})=9 \times \frac{2}{20}+16 \times \frac{2}{20}+25 \times \frac{4}{20}+36 \times \frac{4}{20}+49 \times \frac{4}{20}+64 \times \frac{2}{20}+81 \times \frac{2}{20} \\ =\frac{18}{20}+\frac{32}{20}+\frac{100}{20}+\frac{144}{20}+\frac{196}{20}+\frac{128}{20}+\frac{162}{20}=\frac{780}{20}=39 \\ \therefore \text{ Variance }(X)=E(X^{2})-[E(X)]^{2}=39-(6)^{2}=39-36=3 \end{matrix} $

Solution

Given that: $P(A)=\frac{4}{5}$ and $P(A \cap B)=\frac{7}{10}$

$ \therefore \quad P(B / A)=\frac{P(A \cap B)}{P(A)}=\frac{7 / 10}{4 / 5}=\frac{7}{8} $

Hence, the correct option is (c).

Solution

Given that: $P(A \cap B)=\frac{7}{10}$ and $P(B)=\frac{17}{20}$

$ \therefore \quad P(A / B)=\frac{P(A \cap B)}{P(B)}=\frac{7 / 10}{17 / 20}=\frac{14}{17} $

Hence, the correct option is $(a)$.

Solution

Here, $P(A)=\frac{3}{10}, P(B)=\frac{2}{5}$ and $P(A \cup B)=\frac{3}{5}$

$ \begin{aligned} & P(A \cup B)=P(A)+P(B)-P(A \cap B) \\ & \Rightarrow \quad \frac{3}{5}=\frac{3}{10}+\frac{2}{5}-P(A \cap B) \\ & \Rightarrow \quad P(A \cap B)=\frac{3}{10}+\frac{2}{5}-\frac{3}{5}=\frac{3+4-6}{10}=\frac{1}{10} \\ & \text{ Now } P(A / B)+P(B / A)=\frac{P(A \cap B)}{P(B)}+\frac{P(A \cap B)}{P(A)} \\ & =\frac{1 / 10}{2 / 5}+\frac{1 / 10}{3 / 10}=\frac{1}{4}+\frac{1}{3}=\frac{7}{12} \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Given that: $P(A)=\frac{2}{5}, P(B)=\frac{3}{10}$ and $P(A \cap B)=\frac{1}{5}$

$ \begin{aligned} & P(A^{\prime})=1-\frac{2}{5}=\frac{3}{5}, P(B^{\prime})=1-\frac{3}{10}=\frac{7}{10} \\ & \text{ and } P(A^{\prime} \cap B^{\prime})=1-P(A \cup B)=1-[P(A)+P(B)-P(A \cap B)] \\ &=1-[\frac{2}{5}+\frac{3}{10}-\frac{1}{5}]=1-[\frac{1}{5}+\frac{3}{10}]=1-\frac{5}{10}=\frac{1}{2} \\ & \therefore \quad P(A^{\prime} / B^{\prime})=\frac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\frac{1 / 2}{7 / 10}=\frac{5}{7} \\ & \text{ and } P(B^{\prime} / A^{\prime})=\frac{P(A^{\prime} \cap B^{\prime})}{P(A^{\prime})}=\frac{1 / 2}{3 / 5}=\frac{5}{6} \\ & \therefore P(A^{\prime} / B^{\prime}) \cdot P(B^{\prime} / A^{\prime})=\frac{5}{7} \times \frac{5}{6}=\frac{25}{42} \end{aligned} $

Hence, the correct option is (c).

Solution

Given that: $P(A)=\frac{1}{2}, P(B)=\frac{1}{3}$ and $P(A / B)=\frac{1}{4}$

$ \begin{aligned} P(A / B) & =\frac{P(A \cap B)}{P(B)} \\ \frac{1}{4} & =\frac{P(A \cap B)}{1 / 3} \Rightarrow P(A \cap B)=\frac{1}{4} \times \frac{1}{3}=\frac{1}{12} \end{aligned} $

Now $\quad P(A^{\prime} \cap B^{\prime})=1-P(A \cup B)$

$ =1-[P(A)+P(B)-P(A \cap B)] $

$=1-[\frac{1}{2}+\frac{1}{3}-\frac{1}{12}]=1-[\frac{5}{6}-\frac{1}{12}]=1-\frac{9}{12}=\frac{3}{12}=\frac{1}{4}$

Hence, the correct option is (c).

Solution

Given that: $P(A)=0.4, P(B)=0.8$ and $P(B / A)=0.6$

$ \begin{aligned} P(B / A)=\frac{P(A \cap B)}{P(A)} & \Rightarrow 0.6=\frac{P(A \cap B)}{0.4} \\ \therefore \quad P(A \cap B) & =0.6 \times 0.4=0.24 \\ P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ & =0.4+0.8-0.24=1.20-0.24=0.96 \end{aligned} $

Hence, the correct option is (d).

Solution

Given that: $A=\phi$ and $B \neq \phi$,

then

$ P(A / B)=\frac{P(A \cap B)}{P(B)} $

Hence, the correct option is (b).

Solution

Given that: $P(A)=0.4, P(B)=0.3$ and $P(A \cup B)=0.5$

$ \begin{aligned} P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ 0.5 & =0.4+0.3-P(A \cap B) \\ P(A \cap B) & =0.4+0.3-0.5=0.2 \\ \therefore \quad P(B^{\prime} \cap A) & =P(A)-P(A \cap B) \\ & =0.4-0.2=0.2=\frac{1}{5} \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Given that: $P(B)=\frac{3}{5}, P(A / B)=\frac{1}{2}$ and $P(A \cup B)=\frac{4}{5}$

We know that $P(A / B)=\frac{P(A \cap B)}{P(B)} \Rightarrow \frac{1}{2}=\frac{P(A \cap B)}{3 / 5}$

$\therefore \quad P(A \cap B)=\frac{3}{10}$

Now $\quad P(A \cup B)=P(A)+P(B)-P(A \cap B)$

$ \begin{aligned} \frac{4}{5} & =P(A)+\frac{3}{5}-\frac{3}{10} \\ \Rightarrow \quad P(A) & =\frac{4}{5}-\frac{3}{5}+\frac{3}{10}=\frac{1}{5}+\frac{3}{10}=\frac{5}{10}=\frac{1}{2} \end{aligned} $

Hence, the correct option is (c).

Solution

According to Exercise 64, we have

$ \begin{aligned} & P(B)=\frac{3}{5}, P(A / B)=\frac{1}{2}, P(A \cup B)=\frac{4}{5} \\ & P(B / A^{\prime})=\frac{P(B \cap A^{\prime})}{P(A^{\prime})}=\frac{P(B)-P(A \cap B)}{1-P(A)}=\frac{\frac{3}{5}-\frac{3}{10}}{1-\frac{1}{2}}=\frac{\frac{3}{10}}{\frac{1}{2}}=\frac{3}{5} \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Given that: $P(B)=\frac{3}{5}, P(A / B)=\frac{1}{2}$ and $P(A \cup B)=\frac{4}{5}$

$ \begin{aligned} P(A / B) & =\frac{P(A \cap B)}{P(B)} \\ \Rightarrow \quad \frac{1}{2} & =\frac{P(A \cap B)}{3 / 5} \Rightarrow P(A \cap B)=\frac{3}{10} \\ P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ \frac{4}{5} & =P(A)+\frac{3}{5}-\frac{3}{10} \\ \therefore \quad P(A) & =\frac{4}{5}-\frac{3}{5}+\frac{3}{10}=\frac{1}{5}+\frac{3}{10}=\frac{5}{10}=\frac{1}{2} \end{aligned} $

Now $P(A \cup B)^{\prime}+P(A^{\prime} \cup B)$

$ \begin{aligned} & =1-P(A \cup B)+1-P(A \cap B^{\prime}) \\ & =2-\frac{4}{5}-P(A) \cdot P(B^{\prime}) \\ & =\frac{6}{5}-\frac{1}{2} \cdot(1-\frac{3}{5})=\frac{6}{5}-\frac{1}{2} \times \frac{2}{5}=\frac{6}{5}-\frac{1}{5}=\frac{5}{5}=1 \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Given that: $P(A)=\frac{7}{13}, P(B)=\frac{9}{13}$ and $P(A \cap B)=\frac{4}{13}$

$ P(A^{\prime} / B)=\frac{P(A^{\prime} \cap B)}{P(B)}=\frac{P(B)-P(A \cap B)}{P(B)}=\frac{\frac{9}{13}-\frac{4}{13}}{\frac{9}{13}}=\frac{\frac{5}{13}}{\frac{9}{13}}=\frac{5}{9} $

Hence, the correct option is $(d)$.

Solution

Given that: $P(A)>0$ and $P(B) \neq 1$

$ \therefore \quad P(A^{\prime} / B^{\prime})=\frac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\frac{1-P(A \cup B)}{P(B^{\prime})} $

Hence, the correct option is (c).

Solution

Given that: A and B are independent events

such that

$ \begin{aligned} & P(A)=\frac{3}{5} \quad \therefore P(A^{\prime})=1-\frac{3}{5}=\frac{2}{5} \\ & P(B)=\frac{4}{9} \quad \therefore P(B^{\prime})=1-\frac{4}{9}=\frac{5}{9} \end{aligned} $

$ \therefore \quad P(A^{\prime} \cap B^{\prime})=P(A^{\prime}) \cdot P(B^{\prime})=\frac{2}{5} \cdot \frac{5}{9}=\frac{2}{9} $

Hence, the correct option is $(d)$.

Solution

For independent events $A$ and $B, P(A) \cdot P(B)=P(A \cap B)$

So, they will not be mutually exclusive.

If $P(A)+P(B)=1$, they are exhaustive events and for independent events $A$ and $P(A \cap B) \neq 0$.

Hence, the correct option is $(d)$.

Solution

Given that: $P(A)=\frac{3}{8}, P(B)=\frac{5}{8}$ and $P(A \cup B)=\frac{3}{4}$

$ \begin{matrix} \therefore & P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ \frac{3}{4} & =\frac{3}{8}+\frac{5}{8}-P(A \cap B) \\ \Rightarrow \quad P(A \cap B) & =\frac{3}{8}+\frac{5}{8}-\frac{3}{4}=\frac{1}{4} \end{matrix} $

$ \begin{aligned} \text{ Now } P(A / B) \cdot P(A^{\prime} / B) & =\frac{P(A \cap B)}{P(B)} \cdot \frac{P(A^{\prime} \cap B)}{P(B)} \\ & =\frac{P(A \cap B)}{P(B)} \cdot \frac{P(B)-P(A \cap B)}{P(B)} \\ & =\frac{\frac{1}{5}}{\frac{5}{8}} \cdot \frac{(\frac{5}{8}-\frac{1}{4})}{\frac{5}{8}}=\frac{2}{5} \cdot \frac{3}{5}=\frac{6}{25} \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Since $A$ and $B$ are two independent events

$ \therefore \quad P(A \cap B)=P(A) \cdot P(B) $

Hence, the correct option is (c).

Solution

Given that: $E$ and $F$ are independent events such that $P(E)=0.3$ and $P(E \cup F)=0.5$

$ \begin{matrix} P(E \cup F) =P(E)+P(F)-P(E \cap F) \\ 0.5 =0.3+P(F)-P(E) \cdot P(F) \\ \Rightarrow \quad 0.5-0.3 =P(F)[1-P(E)] \Rightarrow 0.2=P(F)(1-0.3) \\ \Rightarrow \quad 0.2 =P(F) \cdot(0.7) \\ \therefore \quad P(F) =\frac{0.2}{0.7}=\frac{2}{7} \\ \\ \text{ Now } P(E / F)-P(F / E) =\frac{P(E \cap F)}{P(F)}-\frac{P(E \cap F)}{P(E)} \\ =\frac{P(E) \cdot P(F)}{P(F)}-\frac{P(E) \cdot P(F)}{P(E)} =P(E)-P(F)=\frac{3}{10}-\frac{2}{7}=\frac{1}{70} \end{matrix} $

Hence, the correct option is (c).

Solution

Given that: Bag contains 5 red and 3 blue balls.

Probability of getting exactly one red ball if 3 balls are randomly drawn without replacement

$=P(R) \cdot P(B) \cdot P(B)+P(B) \cdot P(R) \cdot P(B)+P(B) \cdot P(B) \cdot P(R)$

$=\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{2}{6}+\frac{3}{8} \cdot \frac{5}{7} \cdot \frac{2}{6}+\frac{3}{8} \cdot \frac{2}{7} \cdot \frac{5}{6}=\frac{30}{336}+\frac{30}{336}+\frac{30}{336}=\frac{90}{336}=\frac{15}{56}$

Hence, the correct option is (c).

Solution

According to Question 74,

Let $E_1$ be the event that first ball is red.

$E_2$ be the event that exactly two of the three balls are red.

$\therefore \quad P(E_1)=P(R) \cdot P(R) \cdot P(B)+P(R) \cdot P(R) \cdot P(R)+P(R) \cdot P(B) \cdot P(R)$ $+P(R) \cdot P(B) \cdot P(B)$

$=\frac{5}{8} \cdot \frac{4}{7} \cdot \frac{3}{6}+\frac{5}{8} \cdot \frac{4}{7} \cdot \frac{3}{6}+\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{4}{6}+\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{2}{6}$

$=\frac{60}{336}+\frac{60}{336}+\frac{60}{336}+\frac{30}{336}=\frac{210}{336}$

$P(E_1 \cap E_2)=P(R) \cdot P(B) \cdot P(R)+P(R) \cdot P(R) \cdot P(B)$

$=\frac{5}{8} \cdot \frac{3}{7} \cdot \frac{4}{6}+\frac{5}{8} \cdot \frac{4}{7} \cdot \frac{3}{6}=\frac{60}{336}+\frac{60}{336}=\frac{120}{336}$

$\therefore P(E_2 / E_1)=\frac{P(E_1 \cap E_2)}{P(E_1)}=\frac{120 / 336}{210 / 336}=\frac{4}{7}$

Hence, the correct option is $(b)$.

Solution

Given that: $P(A)=0.4, P(B)=0.3$ and $P(C)=0.2$

Also $P(\overline{A})=1-0.4=0.6, P(\overline{B})=1-0.3=0.7$

and $P(\bar{{}C})=1-0.2=0.8$

$\therefore$ Probabilities of two hits

$=P(A) \cdot P(B) \cdot P(\overline{C})+P(A) \cdot P(\overline{B}) \cdot P(C)+P(\overline{A}) \cdot P(B) \cdot P(C)$

$=0.4 \times 0.3 \times 0.8+0.4 \times 0.7 \times 0.2+0.6 \times 0.3 \times 0.2$

$=0.096+0.056+0.036=0.188$

Hence, the correct option is $(b)$.

Solution

Let $G$ denotes the girl and $B$ denotes the boy of the given family.

$\text{So}n(S)=\{(BGG),(GBG),(GGB),(GBB),(BGB),(BBG),(BBB), (GGG)\}$

Let $E_1$ be the event that the family has alteast one girl.

$\therefore E_1=\{(BGG),(GBG),(GGB),(GBB),(BGB),(BBG),(GGG)\}$

Let $E_2$ be the event that the eldest child is a girl.

$ \begin{aligned} & \therefore \quad E_2={(GBG),(GGB),(GBB),(GGG)} \\ & (E_1 \cap E_2)={(GBB),(GGB),(GBG),(GGG)} \\ & \therefore P(E_2 / E_1)=\frac{P(E_1 \cap E_2)}{P(E_1)}=\frac{4 / 8}{7 / 8}=\frac{4}{7} \end{aligned} $

Hence, the correct option is $(d)$.

Solution

Let $E_1$ be the event of getting even number on the die. $E_2$ be the event of selecting a spade card.

$\therefore P(E_1)=\frac{3}{6}=\frac{1}{2}$ and $P(E_2)=\frac{13}{52}=\frac{1}{4}$

So $\quad P(E_1 \cap E_2)=P(E_1) \cdot P(E_2)=\frac{1}{2} \cdot \frac{1}{4}=\frac{1}{8}$

Hence, the correction option is (c).

Solution

Probability of drawing 2 green and 1 blue balls $=P(G) \cdot P(G) \cdot P(B)+P(G) \cdot P(B) \cdot P(G)+P(B) \cdot P(G) \cdot P(G)$

$=\frac{3}{8} \cdot \frac{2}{7} \cdot \frac{2}{6}+\frac{3}{8} \cdot \frac{2}{7} \cdot \frac{2}{6}+\frac{2}{8} \cdot \frac{3}{7} \cdot \frac{2}{6}=\frac{12}{336}+\frac{12}{336}+\frac{12}{336}=\frac{36}{336}=\frac{3}{28}$

Hence, the correct option is $(a)$.

Solution

Required probability $=P($ dead $) \cdot P($ dead $)$

$ =\frac{3}{8} \cdot \frac{2}{7}=\frac{3}{28} $

Hence, the correct option is $(d)$.

Solution

Here, $n=8, p=\frac{1}{2}, q=1-\frac{1}{2}=\frac{1}{2}$ and $r=3$

We know that $P(x=r)={ }^{n} C_r p^{r} . q^{n-r}$

$ \begin{aligned} \therefore \quad P(x=3) & ={ }^{8} C_3(\frac{1}{2})^{3}(\frac{1}{2})^{8-3} \\ & =\frac{8 !}{3 ! \cdot 5 !} \cdot(\frac{1}{2})^{3}(\frac{1}{2})^{5}=56 \cdot(\frac{1}{2})^{8}=56 \cdot \frac{1}{256}=\frac{7}{32} \end{aligned} $

Hence, the correct option is $(b)$.

Solution

Let $E_1$ be the event showing the sum of the numbers on the two dice was less than 6 and $E_2$ be the event that the sum of the numbers is 3 .

$ \begin{aligned} & \therefore \quad E_1=\{(1,1),(1,2),(2,1),(1,3),(3,1),(1,4),(4,1), \\ &(2,2),(2,3),(3,2)\} \\ & \text{ and } \quad n(E_1)=10 \\ & E_2={(1,2),(2,1)} \Rightarrow n(E_2)=2 \text{ and } n(E_1 \cap E_2)=2 \end{aligned} $

$\therefore$ Required probability

$ P(E_2 / E_1)=\frac{n(E_1 \cap E_2)}{n(E_1)}=\frac{2}{10}=\frac{1}{5} $

Hence, the correct option is (c).

Solution

We know that for a Binomial distribution, the outcomes must not be dependent on each other.

Hence, the correct option is (c).

Solution

Probability of getting Queen $=\frac{4}{52}$

So, the required probability

$ \begin{aligned} & =P(\text{ Queen }) \cdot P(\text{ Queen }) \\ & =\frac{4}{52} \cdot \frac{4}{52}=\frac{1}{13} \cdot \frac{1}{13} \quad \text{ (with replacement) } \end{aligned} $

Hence, the correct option is $(a)$.

Solution

Here, $n=10, p=\frac{1}{2}$ and $q=\frac{1}{2} \quad$ (for true/false questions) and $r \geq 8$ i.e. $8,9,10$

$ \begin{aligned} \therefore P(X \geq 8) & =P(x=8)+P(x=9)+P(x=10) \\ & ={ }^{10} C_8(\frac{1}{2})^{8}(\frac{1}{2})^{2}+{ }^{10} C_9(\frac{1}{2})^{9}(\frac{1}{2})+{ }^{10} C _{10}(\frac{1}{2})^{10}(\frac{1}{2})^{0} \\ & =45 \cdot(\frac{1}{2})^{10}+10 \cdot(\frac{1}{2})^{10}+(\frac{1}{2})^{10}=(\frac{1}{2})^{10}(45+10+1) \\ & =56 \times \frac{1}{1024}=\frac{7}{128} \end{aligned} $

Hence, the correct option is (b).

Solution

Given that: $\overline{P}=0.3 \therefore p=0.7$ and $q=1-0.7=0.3$ $n=5$ and $r=4$

We know that

$ \begin{aligned} & P(X=r)={ }^{n} C_r(p)^{r} \cdot(q)^{n-r} \\ \therefore \quad & P(x=4)={ }^{5} C_4(0.7)^{4}(0.3)^{5-4}={ }^{5} C_4(0.7)^{4}(0.3) \end{aligned} $

Hence, the correct option is (a).

Solution

We know that $\sum _{i=1}^{n} P(X_i)=1$

$ \begin{aligned} \therefore \quad \frac{5}{k}+\frac{7}{k}+\frac{9}{k}+\frac{11}{k} & =1 \\ \frac{32}{k} & =1 \Rightarrow k=32 . \end{aligned} $

Hence, the correct option is (c).

Solution

We know that:

$ \begin{aligned} E(X) & =\sum _{i=1}^{n} X_i P_i \\ & =(-4)(0.1)+(-3)(0.2)+(-2)(0.3)+(-1)(0.2)+0(0.2) \\ & =-0.4-0.6-0.6-0.2=-1.8 \end{aligned} $

Hence, the correct option is $(d)$.

Solution

We know that

$ \begin{aligned} E(X^{2}) & =\sum _{i=1}^{n} P_i X_i^{2} \\ & =1 \times \frac{1}{10}+4 \times \frac{1}{5}+9 \times \frac{3}{10}+16 \times \frac{2}{5} \end{aligned} $

$ =\frac{1}{10}+\frac{4}{5}+\frac{27}{10}+\frac{32}{5}=\frac{28}{10}+\frac{36}{5}=\frac{100}{10}=10 $

Hence, the correct option is (d).

Solution

$\quad P(X=r)={ }^{n} C_r p^{r} q^{n-r}=\frac{n !}{r !(n-r) !} p^{r} \cdot(1-p)^{n-r}$

$ \begin{aligned} P(X=n-r) & ={ }^{n} C _{n-r} p^{n-r} \cdot(q)^{n-(n-r)}={ }^{n} C _{n-r} p^{n-r} \cdot q^{r} \\ & =\frac{n !}{(n-r) !(n-n+r) !} p^{n-r} q^{r}=\frac{n !}{(n-r) ! r !} \cdot p^{n-r} \cdot q^{r} \end{aligned} $

Now $\frac{P(x=r)}{P(x=n-r)}=\frac{\frac{n !}{r !(n-r) !} \cdot p^{r} \cdot(1-p)^{n-r}}{\frac{n !}{r !(n-r) !} \cdot p^{n-r} \cdot(1-p)^{r}}=\frac{(\frac{1-p}{p})^{n-r}}{(\frac{1-p}{p})^{r}}$

The above expression will be independent of $n$ and $r$ if

$ (\frac{1-p}{p})=1 \Rightarrow \frac{1}{p}=2 \Rightarrow p=\frac{1}{2} $

Hence, the correct option is (a).

Solution

Let $E_1$ be the event that the student fails in Physics and $E_2$ be the event that she fails in Mathematics.

$\therefore \quad P(E_1)=\frac{30}{100}, P(E_2)=\frac{25}{100}$ and $P(E_1 \cap E_2)=\frac{10}{100}$

$\therefore P(E_1 / E_2)=\frac{P(E_1 \cap E_2)}{P(E_2)}=\frac{10 / 100}{25 / 100}=\frac{2}{5}$

Hence, the correct option is (b).

Solution

Let $E_1$ be the event that both of them solve the problem.

$\therefore \quad P(E_1)=\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}$

and $E_2$ be the event that both of them same incorrectly the problem.

$\therefore \quad P(E_2)=(1-\frac{1}{3}) \times(1-\frac{1}{4})=\frac{2}{3} \times \frac{3}{4}=\frac{1}{2}$

Let $H$ be the event that both of them get the same answer.

Here, $P(H / E_1)=1, P(H / E_2)=\frac{1}{20}$

$\therefore P(E_1 / H)=\frac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)}$

$=\frac{\frac{1}{12} \times 1}{\frac{1}{12} \times 1+\frac{1}{2} \times \frac{1}{20}}=\frac{\frac{1}{12}}{\frac{1}{12}+\frac{1}{40}}=\frac{\frac{1}{12}}{\frac{10+3}{120}}=\frac{1 / 12}{13 / 120}=\frac{10}{13}$

Hence, the correct option is (d).

Solution

Here, $n=5, p=\frac{10}{100}=\frac{1}{10}$ and $q=1-\frac{1}{10}=\frac{9}{10}$ and $r \leq 1$

We know that

$ \text{ So } \quad \begin{aligned} P(X=r) & ={ }^{n} C_r p^{r} q^{n-r} \\ P(x \leq 1) & =P(x=0)+P(x=1) \\ & ={ }^{5} C_0(\frac{1}{10})^{0}(\frac{9}{10})^{5}+{ }^{5} C_1(\frac{1}{10})(\frac{9}{10})^{4} \end{aligned} $

$ =(\frac{9}{10})^{5}+\frac{5}{10}(\frac{9}{10})^{4}=(\frac{9}{10})^{5}+\frac{1}{2}(\frac{9}{10})^{4} $

Hence, the correct option is (d).

Solution

False

Solution

True

Solution

False

Solution

False

Solution

True

Solution

True $\qquad [\because E(X)=\sum X_i P(X_i)]$

Solution

True $\quad[\because P(A^{\prime} \cup B)=1-P(A \cap B^{\prime})=1-P(A) \cdot P(B^{\prime})]$

Solution

True

Solution

False

$ \begin{matrix} {[\because P(B / A)=\frac{P(A \cap B)}{P(A)}=\frac{P(A)+P(B)-P(A \cup B)}{P(A)}}>\frac{1-P(A \cup B)}{P(A)}] \end{matrix} $

Solution

True

Since $P$ (atleast two of $A, B$ and $C$ occur)

$ \begin{aligned} & =p \times p \times(1-p)+(1-p) \cdot p \cdot p+p(1-p) \cdot p+p \cdot p \cdot p \\ & =3 p^{2}(1-p)+p^{3}=3 p^{2}-3 p^{3}+p^{3}=3 p^{2}-2 p^{3} \end{aligned} $

Solution

Given that: $P(A)=p, P(B)=\frac{1}{3}$ and $P(A \cup B)=\frac{5}{9}$

$ \begin{aligned} P(A / B) & =\frac{P(A \cap B)}{P(B)}=p \Rightarrow P(A \cap B)=p \cdot P(B)=p \cdot \frac{1}{3} \\ \text{ and } P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ \frac{5}{9}=p+\frac{1}{3} & -\frac{p}{3} \Rightarrow \frac{5}{9}-\frac{1}{3}=\frac{2 p}{3} \Rightarrow \frac{2}{9}=\frac{2 p}{3} \Rightarrow p=\frac{1}{3} \end{aligned} $

Hence, $p$ is equal to $\frac{1}{3}$.

Solution

Here,

$ P(A^{\prime} \cup B^{\prime})=\frac{2}{3} \text{ and } P(A \cup B)=\frac{5}{9} $

$ \begin{aligned} & \therefore & 1-P(A \cap B) & =\frac{2}{3} \\ & \Rightarrow & P(A \cap B) & =1-\frac{2}{3}=\frac{1}{3} \end{aligned} $

Now $\quad P(A^{\prime})+P(B^{\prime})=1-P(A)+1-P(B)=2-[P(A)+P(B)]$

$ \begin{aligned} & =2-[P(A \cup B)+P(A \cap B)] \\ & =2-[\frac{5}{9}+\frac{1}{3}]=2-\frac{8}{9}=\frac{10}{9} \end{aligned} $

Hence, the value of the filler is $\frac{10}{9}$.

Solution

Given that: $P(X=2)=9 P(X=3)$

$ \Rightarrow{ }^{5} C_2 p^{2} q^{3}=9 .{ }^{5} C_3 p^{3} q^{2} $

$ \begin{matrix} \Rightarrow \frac{1}{9} =\frac{{ }^{5} C_3 p^{3} q^{2}}{{ }^{5} C_2 p^{2} q^{3}} \Rightarrow \frac{1}{9}=\frac{p}{q} \quad[\because{ }^{5} C_3={ }^{5} C_2] \\ \Rightarrow 9 p =q \\ \Rightarrow 9 p =1-p \Rightarrow 9 p+p=1 \Rightarrow 10 p=1 \therefore p=\frac{1}{10} \end{matrix} $

Hence, the value of the filler is $\frac{1}{10}$.

Solution

$\quad Var(X)=E(X^{2})-[E(X)]^{2}$

$=\sum X^{2} P(X)-[\sum X . P(X)]^{2}=\sum p_i x_i^{2}-(\sum p_i x_i)^{2}$

Hence, $Var(X)$ is equal to $\sum p_i x_i^{2}-(\sum p_i x_i)^{2}$.

Solution

$ \begin{matrix} \because \qquad P(A / B) =\frac{P(A \cap B)}{P(B)} \\ \Rightarrow P(A) =\frac{P(A \cap B)}{P(B)} \\ \Rightarrow P(A \cap B) =P(A) \cdot P(B) \end{matrix} $

So, $A$ is independent of $B$.