Solution

We know that $\frac{5 \pi}{6} \notin(-\frac{\pi}{2}, \frac{\pi}{2})$ and $\frac{13 \pi}{6} \notin[0, \pi]$

$\therefore \tan ^{-1}(\tan \frac{5 \pi}{6})+\cos ^{-1}(\cos \frac{13 \pi}{6})$

$=\tan ^{-1}[\tan (\pi-\frac{\pi}{6})]+\cos ^{-1}[\cos (2 \pi+\frac{\pi}{6})]$

$=\tan ^{-1}[\tan (-\frac{\pi}{6})]+\cos ^{-1}(\cos \frac{\pi}{6})$

$=\tan ^{-1}(-\tan \frac{\pi}{6})+\cos ^{-1}(\cos \frac{\pi}{6})$

$=-\tan ^{-1}(\tan \frac{\pi}{6})+\cos ^{-1}(\cos \frac{\pi}{6}) \quad[\because \tan ^{-1}(-x)=-\tan ^{-1} x]$

$=-\frac{\pi}{6}+\frac{\pi}{6}=0$

Hence, $\tan ^{-1}(\tan \frac{5 \pi}{6})+\cos ^{-1}(\cos \frac{13 \pi}{6})=0$

Solution

$\cos [\cos ^{-1}(\frac{-\sqrt{3}}{2})+\frac{\pi}{6}]$

$=\cos [\pi-\cos ^{-1} \frac{\sqrt{3}}{2}+\frac{\pi}{6}][\because \cos ^{-1}(-x)=\pi-\cos ^{-1} x]$

$=\cos [\pi-\frac{\pi /}{6}+\frac{\pi /}{6}]=\cos \pi=-1$

$ \text{ Hence, } \cos [\cos ^{-1}(\frac{-\sqrt{3}}{2})+\frac{\pi}{6}]=-1 \text{. } $

Solution

L.H.S. $\cot (\frac{\pi}{4}-2 \cot ^{-1} 3)$

$=\cot [\tan ^{-1}(1)-2 \tan ^{-1} \frac{1}{3}] \quad[\because \cot ^{-1} x=\tan ^{-1} \frac{1}{x}]$

$=\cot [\tan ^{-1}(1)-\tan ^{-1} \frac{2 \times \frac{1}{3}}{1-(\frac{1}{3})^{2}}][\because 2 \tan ^{-1} x=\tan ^{-1} \frac{2 x}{1-x^{2}}]$

$=\cot [\tan ^{-1}(1)-\tan ^{-1} \frac{\frac{2}{3}}{\frac{8}{9}}]$

$=\cot [\tan ^{-1}(1)-\tan ^{-1} \frac{3}{4}]$

$=\cot [\tan ^{-1}(\frac{1-\frac{3}{4}}{1+1 \times \frac{3}{4}})]=\cot [\tan ^{-1}(\frac{\frac{1}{4}}{\frac{7}{4}})]$

$=\cot [\tan ^{-1} \frac{1}{7}] \quad[\because \tan ^{-1} \frac{1}{x}=\cot ^{-1} x]$

$=\cot [\cot ^{-1}(7)]=7$ R.H.S.

Hence proved.

Solution

$\tan ^{-1}(\frac{-1}{\sqrt{3}})+\cot ^{-1}(\frac{1}{\sqrt{3}})+\tan ^{-1}[\sin (\frac{-\pi}{2})]$ $=-\tan ^{-1}(\frac{1}{\sqrt{3}})+\tan ^{-1}(\sqrt{3})+\tan ^{-1}(-1)$

$ \begin{bmatrix} \because \tan ^{-1}(-x)=-\tan ^{-1} x \\ \tan ^{-1} x=\cot ^{-1}(\frac{1}{x}) \\ \sin (\frac{-\pi}{2})=-1 \end{bmatrix} $

$ =-\frac{\pi}{6}+\frac{\pi}{3}-\frac{\pi}{4}=\frac{-\pi}{12} \quad[\because \tan ^{-1}(-1)=\frac{-\pi}{4}] $

Hence, $\tan ^{-1}(\frac{-1}{\sqrt{3}})+\cot ^{-1}(\frac{1}{\sqrt{3}})+\tan ^{-1}[\sin (\frac{-\pi}{2})]=\frac{-\pi}{12}$

Solution

We know that $\frac{2 \pi}{3} \notin[\frac{-\pi}{2}, \frac{\pi}{2}]$

$ \begin{aligned} \therefore \tan ^{-1}(\tan \frac{2 \pi}{3}) & =\tan ^{-1}[\tan (\pi-\frac{\pi}{3})]=\tan ^{-1}(-\tan \frac{\pi}{3}) \\ & =-\tan ^{-1}(\tan \frac{\pi}{3})[\because \tan ^{-1}(-x)=-\tan ^{-1} x] \\ & =-\frac{\pi}{3} \in[-\frac{\pi}{2}, \frac{\pi}{2}] \end{aligned} $

Hence, $\tan ^{-1}(\tan \frac{2 \pi}{3})=\frac{-\pi}{3}$.

Solution

L.H.S. $2 \tan ^{-1}(-3)=-2 \tan ^{-1}(3)$

$ \begin{aligned} & =-\cos ^{-1}[\frac{1-(3)^{2}}{1+(3)^{2}}][\because 2 \tan ^{-1} x=\cos ^{-1}(\frac{1-x^{2}}{1+x^{2}})] \\ & =-\cos ^{-1}(\frac{1-9}{1+9})=-\cos ^{-1}(\frac{-8}{10}) \\ & =-\cos ^{-1}(\frac{-4}{5})=-[\pi-\cos ^{-1}(\frac{4}{5})]=-\pi+\cos ^{-1} \frac{4}{5} \\ & =-\pi+\tan ^{-1}(\frac{3}{4}) \quad[\because \cos ^{-1} \frac{4}{5}=\tan ^{-1} \frac{3}{4}] \end{aligned} $

$ \begin{matrix} =-\pi+\frac{\pi}{2}-\cot ^{-1}(\frac{3}{4}) & {[\tan ^{-1} x=\frac{\pi}{2}-\cot ^{-1} x]} \\ =\frac{-\pi}{2}-\cot ^{-1}(\frac{3}{4}) & {[\because \tan ^{-1} x=\cot ^{-1} \frac{1}{x}]} \\ =\frac{-\pi}{2}-\tan ^{-1}(\frac{4}{3}) & \\ =\frac{-\pi}{2}+\tan ^{-1}(-\frac{4}{3}) \text{ R.H.S. } & \end{matrix} $

Hence proved.

Solution

$\tan ^{-1} \sqrt{x(x+1)}+\sin ^{-1} \sqrt{x^{2}+x+1}=\frac{\pi}{2}$

$ \text{ Let } \quad \theta=\sin ^{-1} \sqrt{x^{2}+x+1} $

$\therefore \quad \sin \theta=\sqrt{x^{2}+x+1}$

$\Rightarrow \tan \theta=\frac{\sqrt{x^{2}+x+1}}{\sqrt{-x^{2}-x}} \Rightarrow \theta=\tan ^{-1}(\frac{\sqrt{x^{2}+x+1}}{\sqrt{-x^{2}-x}})$

$\Rightarrow \sin ^{-1} \sqrt{x^{2}+x+1}=\tan ^{-1}(\sqrt{\frac{x^{2}+x+1}{-x^{2}-x}})$

So, $\tan ^{-1} \sqrt{x(x+1)}+\tan ^{-1}(\sqrt{\frac{x^{2}+x+1}{-x^{2}-x}})=\frac{\pi}{2}$

$\Rightarrow \tan ^{-1}[\frac{\sqrt{x(x+1)}+\sqrt{\frac{x^{2}+x+1}{-x(x+1)}}}{1-\sqrt{x(x+1)} \times \sqrt{\frac{x^{2}+x+1}{-x(x+1)}}}]=\frac{\pi}{2}$

$\Rightarrow \tan ^{-1}[\frac{\frac{x(x+1)+\sqrt{-(x^{2}+x+1)}}{\sqrt{x(x+1)}}}{1-\sqrt{-(x^{2}+x+1)}}]=\frac{\pi}{2}$ $\Rightarrow \frac{x^{2}+x-\sqrt{-(x^{2}+x+1)}}{[1-\sqrt{-(x^{2}+x+1)}] \sqrt{x^{2}+x}}=\tan \frac{\pi}{2}=\frac{1}{0}$ $\Rightarrow[1-\sqrt{-(x^{2}+x+1)}] \sqrt{x^{2}+x}=0$ $\Rightarrow[1-\sqrt{-(x^{2}+x+1)}]=0$ or $\sqrt{x^{2}+x}=0$

Here, $\sqrt{-(x^{2}+x+1)} \notin R$

$\therefore \sqrt{x^{2}+x}=0$

$\Rightarrow \quad x^{2}+x=0 \Rightarrow x(x+1)=0$

$\Rightarrow \quad x=0$ or $x+1=0 \Rightarrow x=0$ or $x=-1$

Hence the real solutions are $x=0$ and $x=-1$.

Alternate Method

$ \begin{aligned} & \tan ^{-1} \sqrt{x(x+1)}+\sin ^{-1} \sqrt{x^{2}+x+1}=\frac{\pi}{2} \\ & \Rightarrow \tan ^{-1} \sqrt{x^{2}+x}=\frac{\pi}{2}-\sin ^{-1} \sqrt{x^{2}+x+1} \\ & \Rightarrow \tan ^{-1} \sqrt{x^{2}+x}=\cos ^{-1} \sqrt{x^{2}+x+1}[\because \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}] \\ & \Rightarrow \cos ^{-1}[\frac{1}{\sqrt{1+x^{2}+x}}]=\cos ^{-1} \sqrt{x^{2}+x+1} \\ & \Rightarrow \quad \frac{1}{\sqrt{x^{2}+x+1}}=\sqrt{x^{2}+x+1} \quad[\because \tan ^{-1} x=\cos ^{-1} \frac{1}{\sqrt{1+x^{2}}}] \\ & \Rightarrow \quad x^{2}+x+1=1 \quad \Rightarrow x^{2}+x=0 \\ & \Rightarrow \quad x(x+1)=0 \quad \Rightarrow x=0 \text{ or } x+1=0 \\ & \therefore \quad x=0, x=-1 \end{aligned} $

Solution

$\sin (2 \tan ^{-1} \frac{1}{3})+\cos (\tan ^{-1} 2 \sqrt{2})$

$ \begin{aligned} & \Rightarrow \sin [\tan ^{-1}(\frac{2 \times \frac{1}{3}}{1-(\frac{1}{3})^{2}})]+\cos [\cos ^{-1} \frac{1}{\sqrt{1+(2 \sqrt{2})^{2}}}] \\ & {[\because \tan ^{-1} x=\cos ^{-1}(\frac{1}{\sqrt{1+x^{2}}})]} \\ & \Rightarrow \sin [\tan ^{-1}(\frac{\frac{2}{3}}{1-\frac{1}{9}})]+\cos [\cos ^{-1}(\frac{1}{3})] \\ & .\Rightarrow \sin [\tan ^{-1}(\frac{3}{4})]+\frac{1}{3} \Rightarrow \sin ^{-1}(\frac{3}{5})]+\frac{1}{3} \\ & \Rightarrow \frac{3}{5}+\frac{1}{3} \Rightarrow \frac{14}{15} \\ & \text{ Hence, } \sin (2 \tan ^{-1} \frac{1}{3})+\cos (\tan ^{-1} 2 \sqrt{2})=\frac{14}{15} . \end{aligned} $

Solution

$2 \tan ^{-1}(\cos \theta)=\tan ^{-1}(2 cosec \theta)$

$ \begin{aligned} & \Rightarrow \tan ^{-1}(\frac{2 \cos \theta}{1-\cos ^{2} \theta})=\tan ^{-1}(2 cosec \theta) \\ & \Rightarrow \quad[\because 2 \tan ^{-1} x=\tan ^{-1} \frac{2 x}{1-x^{2}}] \\ & \Rightarrow \quad \frac{2 \cos \theta}{1-\cos ^{2} \theta}=2 cosec \theta \Rightarrow \frac{2 \cos \theta}{\sin ^{2} \theta}=\frac{2}{\sin \theta} \\ & \Rightarrow \quad \cos \theta \sin \theta-\sin ^{2} \theta=0 \Rightarrow \sin \theta(\cos \theta-\sin \theta)=0 \\ & \Rightarrow \quad \sin \theta=0 \text{ or } \quad \cos \theta-\sin \theta=0 \\ & \Rightarrow \quad \sin \theta=0 \quad \text{ or } \quad 1-\tan \theta=0 \\ & \Rightarrow \quad \theta=0 \text{ or } \quad \tan \theta=1 \\ & \Rightarrow \quad \theta=0^{\circ} \text{ or } \quad \theta=\frac{\pi}{4} \text{ Hence proved. } \end{aligned} $

Solution

L.H.S. $\cos (2 \tan ^{-1} \frac{1}{7})$

$ \begin{aligned} & =\cos [\cos ^{-1} \frac{1-\frac{1}{49}}{1+\frac{1}{49}}] \quad[\because 2 \tan ^{-1} x=\cos ^{-1} \frac{1-x^{2}}{1+x^{2}}] \\ & =\cos [\cos ^{-1} \frac{48}{50}]=\cos [\cos ^{-1} \frac{24}{25}]=\frac{24}{25} \end{aligned} $

R.H.S. $\sin [4 \tan ^{-1} \frac{1}{3}]$

$ \begin{aligned} & =\sin [2 \tan ^{-1}(\frac{2 \times \frac{1}{3}}{1-\frac{1}{9}})][\because 2 \tan ^{-1} x=\tan ^{-1} \frac{2 x}{1-x^{2}}] \\ & =\sin [2 \tan ^{-1}(\frac{\frac{2}{3}}{\frac{3}{9}})]=\sin [2 \tan ^{-1} \frac{3}{4}] \\ & =\sin [\sin ^{-1} \frac{2 \times \frac{3}{4}}{1+\frac{9}{16}}][\because 2 \tan ^{-1} x=\sin ^{-1} \frac{2 x}{1+x^{2}}] \\ & =\sin [\sin ^{-1} \frac{24}{25}] \Rightarrow \frac{24}{25} \end{aligned} $

L.H.S. = R.H.S. Hence proved.

Solution

Given that $\cos (\tan ^{-1} x)=\sin (\cot ^{-1} \frac{3}{4})$

$ \begin{aligned} \Rightarrow \cos [\cos ^{-1} \frac{1}{\sqrt{1+x^{2}}}]=\sin [\sin ^{-1} \frac{4}{5}] \\ { \begin{bmatrix} \because \tan ^{-1} x=\cos ^{-1}(\frac{1}{\sqrt{1+x^{2}}}) \\ \cot ^{-1} x=\sin ^{-1}(\frac{1}{\sqrt{1+x^{2}}}) \end{bmatrix} } \end{aligned} $

$ \Rightarrow \quad \frac{1}{\sqrt{1+x^{2}}}=\frac{4}{5} $

Squaring both sides we get,

$ \begin{aligned} & \frac{1}{1+x^{2}}=\frac{16}{25} \Rightarrow 1+x^{2}=\frac{25}{16} \\ & \Rightarrow \quad x^{2}=\frac{25}{16}-1=\frac{9}{16} \Rightarrow x= \pm \frac{3}{4} \\ & \text{ Hence, } \quad x=\frac{-3}{4}, \frac{3}{4} \text{. } \end{aligned} $

Solution

L.H.S. $\tan ^{-1}[\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}]$

Put $x^{2}=\cos \theta \quad \therefore \theta=\cos ^{-1} x^{2}$

$\Rightarrow \tan ^{-1}[\frac{\sqrt{1+\cos \theta}+\sqrt{1-\cos \theta}}{\sqrt{1+\cos \theta}-\sqrt{1-\cos \theta}}]$

$\Rightarrow \tan ^{-1}[\frac{\sqrt{2 \cos ^{2} \theta / 2}+\sqrt{2 \sin ^{2} \theta / 2}}{\sqrt{2 \cos ^{2} \theta / 2}-\sqrt{2 \sin ^{2} \theta / 2}}] \begin{cases} \because 1+\cos \theta=2 \cos ^{2} \theta / 2 \\ 1-\cos \theta=2 \sin ^{2} \theta / 2 \end{cases} $

$\Rightarrow \tan ^{-1}[\frac{\cos \theta / 2+\sin \theta / 2}{\cos \theta / 2-\sin \theta / 2}]$

$\Rightarrow \tan ^{-1}[\frac{1+\tan \theta / 2}{1-\tan \theta / 2}] \quad$ [Dividing the Nr. and Den. by $\cos \theta / 2$ ]

$\Rightarrow \tan [\tan (\frac{\pi}{4} \quad \frac{\theta}{2})] \quad[\because \frac{1+\tan \theta}{1-\tan \theta}=\tan (\frac{\pi}{4}+\theta)]$

$\Rightarrow \frac{\pi}{4}+\frac{\theta}{2} \Rightarrow \frac{\pi}{4}+\frac{1}{2} \cos ^{-1} x^{2}$ R.H.S. $\quad$ [Putting $\theta=\cos ^{-1} x^{2}$ ]

Hence proved.

Solution

Given that $\cos ^{-1}(\frac{3}{5} \cos x+\frac{4}{5} \sin x)$

Put $\quad \frac{3}{5}=\cos y$

$\therefore \quad \sqrt{1-\cos ^{2} y}=\sin y \Rightarrow \sqrt{1-\frac{9}{25}}=\sin y \Rightarrow \frac{4}{5}=\sin y$

$\therefore \cos ^{-1}[\frac{3}{5} \cos x+\frac{4}{5} \sin x]=\cos ^{-1}[\cos y \cos x+\sin y \sin x]$

$=\cos ^{-1}[\cos (y-x)]=y-x$

$=\tan ^{-1} \frac{4}{3}-x$ $\frac{8}{7}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{77}{85}$

Solution

L.H.S. $\sin ^{-1} \frac{8}{17}+\sin ^{-1} \frac{3}{5}$

$ \begin{aligned} & \text{ Using } \sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}[x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}] \\ & \begin{aligned} \sin ^{-1} \frac{8}{17}+ & \sin ^{-1} \frac{3}{5}=\sin ^{-1}[\frac{8}{17} \cdot \sqrt{1-(\frac{3}{5})^{2}}+\frac{3}{5} \cdot \sqrt{1-(\frac{8}{17})^{2}}] \\ & =\sin ^{-1}[\frac{8}{17} \cdot \sqrt{1-\frac{9}{25}}+\frac{3}{5} \cdot \sqrt{1-\frac{64}{289}}] \\ & =\sin ^{-1}[\frac{8}{17} \cdot \sqrt{\frac{16}{25}}+\frac{3}{5} \cdot \sqrt{\frac{225}{289}}] \\ & =\sin ^{-1}[\frac{8}{17} \cdot \frac{4}{5}+\frac{3}{5} \cdot \frac{15}{17}]=\sin ^{-1}[\frac{32}{85}+\frac{45}{85}] \\ & =\sin ^{-1} \frac{77}{85} \text{ R.H.S. Hence proved. } \end{aligned} \end{aligned} $

Solution

Let $\sin ^{-1} \frac{5}{13}=x \quad \Rightarrow \quad \sin x=\frac{5}{13}$

$\Rightarrow \quad \tan x=\frac{5}{12}$

Let $\cos ^{-1} \frac{3}{5}=y \quad \Rightarrow \quad \cos y=\frac{3}{5}$

$\Rightarrow \quad \tan y=\frac{4}{3}$

Now $\quad \tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}$

$\Rightarrow \quad \tan (x+y)=\frac{\frac{5}{12}+\frac{4}{3}}{1-\frac{5}{12} \times \frac{4}{3}}=\frac{\frac{15+48}{36}}{\frac{36-20}{36}}=\frac{63}{16}$

$\Rightarrow \quad x+y=\tan ^{-1} \frac{63}{16}$

$\therefore \sin ^{-1} \frac{5}{13}+\cos ^{-1} \frac{3}{5}=\tan ^{-1} \frac{63}{16}$ Hence proved.

Solution

$\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\tan ^{-1}[\frac{\frac{1}{4}+\frac{2}{9}}{1-\frac{1}{4} \times \frac{2}{9}}]$

$[\because \tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}(\frac{x+y}{1-x y})]$

$\Rightarrow \tan ^{-1}[\frac{\frac{9+8}{36}}{\frac{36-2}{36}}]=\tan ^{-1}[\frac{17}{34}]$

Let $\quad \tan ^{-1}[\frac{17}{34}]=x$

$\therefore \quad \tan x=\frac{17}{34}=\frac{1}{2}$

$ \begin{aligned} \sin x & =\frac{1}{\sqrt{5}} \\ \therefore \quad \tan ^{-1} \frac{1}{2} & =\sin ^{-1} \frac{1}{\sqrt{5}} \text{ R.H.S. } \end{aligned} $

Hence, $\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\sin ^{-1} \frac{1}{\sqrt{5}}$

Solution

$4 \tan ^{-1} \frac{1}{5}-\tan ^{-1} \frac{1}{239}$

$\Rightarrow 2 \cdot(2 \tan ^{-1} \frac{1}{5})-\tan ^{-1} \frac{1}{239}$

$\Rightarrow 2[\tan ^{-1} \frac{2 \times \frac{1}{5}}{1-\frac{1}{25}}]-\tan ^{-1} \frac{1}{239} \quad[2 \tan ^{-1} x=\tan ^{-1} \frac{2 x}{1-x^{2}}]$

$\Rightarrow 2 \tan ^{-1} \frac{5}{12}-\tan ^{-1} \frac{1}{239} \Rightarrow \tan ^{-1}(\frac{2 \times \frac{5}{12}}{1-\frac{25}{144}})-\tan ^{-1}(\frac{1}{239})$

$\Rightarrow \tan ^{-1}(\frac{120}{119})-\tan ^{-1}(\frac{1}{239})$

$\Rightarrow \tan ^{-1}[\frac{\frac{120}{119}-\frac{1}{239}}{1+\frac{120}{119} \times \frac{1}{239}}][\because \tan ^{-1} x-\tan ^{-1} y=\tan ^{-1} \frac{x-y}{1+x y}]$

$\Rightarrow \tan ^{-1}[\frac{120 \times 239-119}{119 \times 239+120}] \Rightarrow \tan ^{-1}[\frac{28680-119}{28441+120}]$

$\Rightarrow \tan ^{-1}[\frac{28561}{28561}]=\tan ^{-1}(1)=\frac{\pi}{4}$

Solution

To prove that $\tan (\frac{1}{2} \sin ^{-1} \frac{3}{4})=\frac{4-\sqrt{7}}{3}$ L.H.S. Let $\frac{1}{2} \sin ^{-1} \frac{3}{4}=\tan ^{-1} \theta$ $[\therefore \tan (\tan ^{-1} \theta)=\theta]$

$ \begin{aligned} & \Rightarrow \quad \sin ^{-1} \frac{3}{4}=2 \tan ^{-1} \theta \Rightarrow \sin ^{-1} \frac{3}{4}=\sin ^{-1}(\frac{2 \theta}{1+\theta^{2}}) \\ & {[\because 2 \tan ^{-1} x=\sin ^{-1} \frac{2 x}{1+x^{2}}]} \\ & \Rightarrow \quad \frac{2 \theta}{1+\theta^{2}}=\frac{3}{4} \Rightarrow 3+3 \theta^{2}=8 \theta \\ & \Rightarrow \quad 3 \theta^{2}-8 \theta+3=0 \\ & \Rightarrow \quad \theta=\frac{-(-8) \pm \sqrt{(-8)^{2}-4 \times 3 \times 3}}{2 \times 3} \\ & =\frac{8 \pm \sqrt{64-36}}{6}=\frac{8 \pm \sqrt{28}}{6}=\frac{8 \pm 2 \sqrt{7}}{6}=\frac{2(4 \pm \sqrt{7})}{6} \\ & \Rightarrow \quad \theta=\frac{4 \pm \sqrt{7}}{3} \\ & \therefore \quad \theta=\frac{4+\sqrt{7}}{3} \text{ or } \frac{4-\sqrt{7}}{3} \\ & \theta=\frac{4+\sqrt{7}}{3} \text{ is ignored. } \\ & \text{ Because } \frac{-\pi}{2} \leq \sin ^{-1} \frac{3}{4} \leq \frac{\pi}{2} \\ & \Rightarrow \frac{-\pi}{4} \leq \frac{1}{2} \sin ^{-1} \frac{3}{4} \leq \frac{\pi}{4} \\ & \Rightarrow \tan (\frac{-\pi}{4}) \leq \tan (\frac{1}{2} \sin ^{-1} \frac{3}{4}) \leq \tan (\frac{\pi}{4}) \\ & \Rightarrow-1 \leq \tan (\frac{1}{2} \sin ^{-1} \frac{3}{4}) \leq 1 \end{aligned} $

Solution

If $a_1, a_2, a_3, \ldots, a_n$ are the terms of an arithmetic progression $\therefore d=a_2-a_1=a_3-a_2=a_4-a_3 \ldots$

$ \begin{matrix} \therefore \tan [\tan ^{-1}(\frac{a_2-a_1}{1+a_1 a_2})+\tan ^{-1}(\frac{a_3-a_2}{1+a_2 a_3})+\tan ^{-1}(\frac{a_4-a_3}{1+a_3 a_4})+\ldots. \\ .\ldots+\tan ^{-1}(\frac{a_n-a _{n-1}}{1+a _{n-1} \cdot a_n})] \\ \Rightarrow \tan [(\tan ^{-1} a_2-\tan ^{-1} a_1)+(\tan ^{-1} a_3-\tan ^{-1} a_2)+(\tan ^{-1} a_4-\tan ^{-1} a_3). \\ .+\ldots+(\tan ^{-1} a_n-\tan ^{-1} a _{n-1})] \\ \Rightarrow \tan [\tan ^{-1} a_2-\tan ^{-1} a_1+\tan ^{-1} a_3-\tan ^{-1} a_2+\tan ^{-1} a_4-\tan ^{-1} a_3. \\ \quad[\because \tan ^{-1} \frac{x-y}{1+x y}=\tan ^{-1} x-\tan ^{-1} y] \\ \Rightarrow \tan [\tan ^{-1} a_n-\tan ^{-1} a_1] \quad \quad[\because \tan (\tan ^{-1} x)=x] \\ \Rightarrow \tan [\tan ^{-1}(\frac{a_n-a_1}{1+a_1 a_n})] \Rightarrow \frac{a_n-a_1}{1+a_1 a_n \quad} \end{matrix} $

Solution

Principal value branch of $\cos ^{-1} x$ is $[0, \pi]$. Hence the correct answer is (c).

Solution

Principal value branch of $cosec^{-1} x$ is $[\frac{-\pi}{2}, \frac{\pi}{2}]-{0}$ as $cosec^{-1}(0)=\infty$ (not defined).

Hence, the correct answer is (d).

Solution

Given that $3 \tan ^{-1} x+\cot ^{-1} x=\pi$

$\Rightarrow 2 \tan ^{-1} x+\tan ^{-1} x+\cot ^{-1} x=\pi$

$\Rightarrow 2 \tan ^{-1} x+\frac{\pi}{2}=\pi$

$[\because \tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}]$

$\Rightarrow \quad 2 \tan ^{-1} x=\pi-\frac{\pi}{2} \quad \Rightarrow 2 \tan ^{-1} x=\frac{\pi}{2}$

$\Rightarrow \quad \tan ^{-1} x=\frac{\pi}{4} \quad \Rightarrow \tan ^{-1} x=\tan ^{-1}(1)$

$\therefore \quad x=1$

Hence, the correct answer is $(b)$.

Solution

$\sin ^{-1}[\cos (\frac{33 \pi}{5})]=\sin ^{-1}[\cos (6 \pi+\frac{3 \pi}{5})]$

$ \begin{aligned} & =\sin ^{-1}[\cos \frac{3 \pi}{5}] \quad[\because \cos (2 n \pi+x)=\cos x] \\ & =\sin ^{-1}[\cos (\frac{\pi}{2}+\frac{\pi}{10})] \\ & =\sin ^{-1}[-\sin (\frac{\pi}{10})][\because \cos (\frac{\pi}{2}+\theta)=-\sin \theta] \\ & =\sin ^{-1}[\sin (\frac{-\pi}{10})]=\frac{-\pi}{10} \end{aligned} $

Hence, the correct answer is $(d)$.

Solution

The given function is $\cos ^{-1}(2 x-1)$

Let

$ \begin{aligned} f(x) & =\cos ^{-1}(2 x-1) \\ -1 & \leq 2 x-1 \leq 1 \Rightarrow-1+1 \leq 2 x \leq 1+1 \\ 0 & \leq 2 x \leq 2 \quad \Rightarrow 0 \leq x \leq 1 \end{aligned} $

$\therefore$ domain of the given function is $[0,1]$.

Hence, the correct answer is (a)

Solution

Let

$ f(x)=\sin ^{-1} \sqrt{x-1} $

$\because \sqrt{x-1} \geq 0$ and $-1 \leq \sqrt{x-1} \leq 1$

$ \Rightarrow 0 \leq x-1 \leq 1 \Rightarrow 1 \leq x \leq 2 \Rightarrow x \in[1,2] $

Hence, the correct answer is (a).

Solution

Given that $\cos [\sin ^{-1} \frac{2}{5}+\cos ^{-1} x]=0$

$ \begin{matrix} \Rightarrow \sin ^{-1} \frac{2}{5}+\cos ^{-1} x =\cos ^{-1}(0) \\ \Rightarrow \sin ^{-1} \frac{2}{5}+\cos ^{-1} x =\frac{\pi}{2} \Rightarrow \sin ^{-1} \frac{2}{5}=\frac{\pi}{2}-\cos ^{-1} x \\ \Rightarrow \sin ^{-1} \frac{2}{5} =\sin ^{-1} x[\because \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}] \\ \Rightarrow x =\frac{2}{5} \end{matrix} $

Hence, the correct answer is (b).

Solution

Given that $\sin [2 \tan ^{-1}(0.75)]$

$ \begin{aligned} & =\sin [2 \tan ^{-1} \frac{3}{4}] \\ & =\sin [\sin ^{-1} \frac{2 \times \frac{3}{4}}{1+\frac{9}{16}}][\because 2 \tan ^{-1} x=\sin ^{-1} \frac{2 x}{1+x^{2}}] \\ & =\sin [\sin ^{-1} \frac{\frac{3}{2}}{\frac{25}{16}}]=\sin [\sin ^{-1} \frac{24}{25}] \\ & =\sin [\sin ^{-1}(0.96)] \end{aligned} $

$ =0.96 $

Hence, the correct answer is (c).

Solution

$ \cos ^{-1}(\cos \frac{\pi}{2}) \neq \frac{3 \pi}{2} \quad \because \frac{3 \pi}{2} \notin[0, \pi] $

$\Rightarrow \cos ^{-1}[\cos (\pi+\frac{\pi}{2})] \Rightarrow \cos ^{-1}[-\cos \frac{\pi}{2}] \Rightarrow \cos ^{-1}[0]=\frac{\pi}{2}$

Hence, the correct answer is (a).

Solution

$2 \sec ^{-1} 2+\sin ^{-1} \frac{1}{2}=2 \sec ^{-1}(\sec \frac{\pi}{3})+\sin ^{-1}(\sin \frac{\pi}{6})$

$ =2 \cdot \frac{\pi}{3}+\frac{\pi}{6}=\frac{2 \pi}{3}+\frac{\pi}{6}=\frac{5 \pi}{6} $

Hence, the correct answer is $(b)$.

Solution

Given that $\tan ^{-1} x+\tan ^{-1} y=\frac{4 \pi}{5}$

$ \begin{matrix} \Rightarrow & \frac{\pi}{2}-\cot ^{-1} x+\frac{\pi}{2}-\cot ^{-1} y=\frac{4 \pi}{5} \quad[\because \tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}] \\ \Rightarrow & \pi-(\cot ^{-1} x+\cot ^{-1} y)=\frac{4 \pi}{5} \\ \Rightarrow & \quad \cot ^{-1} x+\cot ^{-1} y=\pi-\frac{4 \pi}{5} \\ \Rightarrow & \quad \cot ^{-1} x+\cot ^{-1} y=\frac{\pi}{5} \end{matrix} $

Hence, the correct answer is (a).

Solution

$\sin ^{-1}(\frac{2 a}{1+a^{2}})+\cos ^{-1}(\frac{1-a^{2}}{1+a^{2}})=\tan ^{-1}(\frac{2 x}{1-x^{2}})$

$ \Rightarrow 2 \tan ^{-1} a+2 \tan ^{-1} a=2 \tan ^{-1} x $

$[\because 2 \tan ^{-1} x=\sin ^{-1} \frac{2 x}{1+x^{2}}=\cos ^{-1} \frac{1-x^{2}}{1+x^{2}}=\tan ^{-1} \frac{2 x}{1-x^{2}}]$

$\Rightarrow \quad 4 \tan ^{-1} a=2 \tan ^{-1} x \Rightarrow 2 \tan ^{-1} a=\tan ^{-1} x$

Hence, the correct answer is (d).

Solution

We have, $\cot [\cos ^{-1}(\frac{7}{25})]$

Let $\quad \cos ^{-1} \frac{7}{25}=\theta$

$\therefore \quad \cos \theta=\frac{7}{25} \Rightarrow \cot \theta=\frac{7}{24}$

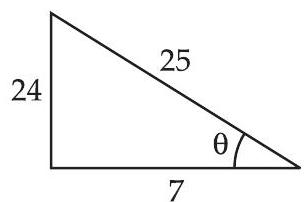
$\therefore \cot [\cos ^{-1}(\frac{7}{25})]=\cot [\cot ^{-1}(\frac{7}{24})]=\frac{}{24}$

Hence, the correct answer is $(d)$.

Solution

We have, $\tan [\frac{1}{2} \cos ^{-1} \frac{2}{\sqrt{5}}]$

$ \begin{aligned} & \text{ Let } \\ & \theta=\frac{1}{2} \cos ^{-1} \frac{2}{\sqrt{5}} \\ & \Rightarrow \quad 2 \theta=\cos ^{-1} \frac{2}{\sqrt{5}} \Rightarrow \cos 2 \theta=\frac{2}{\sqrt{5}} \\ & \Rightarrow \quad \frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}=\frac{2}{\sqrt{5}} \quad[\because \cos 2 \theta=\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}] \\ & \Rightarrow \quad 2+2 \tan ^{2} \theta=\sqrt{5}-\sqrt{5} \tan ^{2} \theta \\ & \Rightarrow \sqrt{5} \tan ^{2} \theta+2 \tan ^{2} \theta=\sqrt{5}-2 \Rightarrow(\sqrt{5}+2) \tan ^{2} \theta=\sqrt{5}-2 \end{aligned} $

$ \begin{matrix} \Rightarrow & \tan ^{2} \theta=\frac{\sqrt{5}-2}{\sqrt{5}+2} \\ \Rightarrow & \tan ^{2} \theta=\frac{(\sqrt{5}-2)(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)} \Rightarrow \tan ^{2} \theta=\frac{(\sqrt{5}-2)^{2}}{5-4} \\ \Rightarrow & \tan \theta= \pm(\sqrt{5}-2) \\ \Rightarrow \quad & \tan \theta=\sqrt{5}-2,[-(\sqrt{5}-2) \text{ is not required }] \end{matrix} $

Hence, the correct answer is $(b)$.

Solution

Here, we have $2 \tan ^{-1} x+\sin ^{-1}(\frac{2 x}{1+x^{2}})$

$ \begin{aligned} & =2 \tan ^{-1} x+2 \tan ^{-1} x \quad[\because 2 \tan ^{-1} x=\sin ^{-1} \frac{2 x}{1+x^{2}}] \\ & =4 \tan ^{-1} x \end{aligned} $

Hence, the correct answer is $(a)$.

Solution

We have $\cos ^{-1} \alpha+\cos ^{-1} \beta+\cos ^{-1} \gamma=3 \pi$

$ \begin{aligned} & \Rightarrow \quad \cos ^{-1} \alpha+\cos ^{-1} \beta+\cos ^{-1} \gamma=\pi+\pi+\pi \\ & \Rightarrow \quad \cos ^{-1} \alpha=\pi, \cos ^{-1} \beta=\pi \text{ and } \cos ^{-1} \gamma=\pi \\ & \Rightarrow \quad \alpha=\cos \pi, \beta=\cos \pi \text{ and } \gamma=\cos \pi \\ & \therefore \quad \alpha=-1, \beta=-1 \text{ and } \gamma=-1 \\ & \text{ Which gives } \alpha=\beta=\gamma=-1 \\ & \text{ So } \quad \alpha(\beta+\gamma)+\beta(\gamma+\alpha)+\gamma(\alpha+\beta) \\ & \Rightarrow \quad(-1)(-1-1)+(-1)(-1-1)+(-1)(-1-1) \\ & \Rightarrow \quad(-1)(-2)+(-1)(-2)+(-1)(-2) \Rightarrow 2+2+2 \Rightarrow 6 \end{aligned} $

Hence, the correct answer is (c).

Solution

We have $\sqrt{1+\cos 2 x}=\sqrt{2} \cos ^{-1}(\cos x)$

$ \begin{matrix} \Rightarrow & \sqrt{2 \cos ^{2} x}=\sqrt{2} x \\ \Rightarrow & \sqrt{2} \cos x & =\sqrt{2} x \Rightarrow \cos x=x \end{matrix} $

Which does not satisfy for any value of $x$.

Hence, the correct answer is $(d)$.

Solution

Here, given that $\cos ^{-1} x>\sin ^{-1} x$

$ \begin{matrix} \Rightarrow & \sin [\cos ^{-1} x]>x \\ \Rightarrow & \sin [\sin ^{-1} \sqrt{1-x^{2}}]>x \Rightarrow \sqrt{1-x^{2}}>x \\ \Rightarrow & x<\sqrt{1-x^{2}} \Rightarrow x^{2}<1-x^{2} \Rightarrow 2 x^{2}<1 \\ \Rightarrow & x^{2}<\frac{1}{2} \Rightarrow x< \pm \frac{1}{\sqrt{2}} \end{matrix} $

We know that $-1 \leq x \leq 1$

So $-1 \leq x<\frac{1}{\sqrt{2}}$.

Hence, the correct answer is (c).

Solution

Let $\cos ^{-1}(-\frac{1}{2})=x \quad \Rightarrow \quad \cos x=-\frac{1}{2}$

$ \begin{aligned} & \Rightarrow & \cos x & =\cos (-\frac{\pi}{3}) \Rightarrow \cos x=\cos (\pi-\frac{\pi}{3})=\cos \frac{2 \pi}{3} \\ & \therefore & x & =\frac{2 \pi}{3} \in[0, \pi] \end{aligned} $

Hence, Principal value of $\cos ^{-1}(-\frac{1}{2})=\frac{2 \pi}{3}$.

Solution

$\quad \sin ^{-1}(\sin \frac{3 \pi}{5}) \neq \frac{3 \pi}{5}$ as $\frac{3 \pi}{5} \notin[\frac{-\pi}{2}, \frac{\pi}{2}]$

So $\sin ^{-1}(\sin \frac{3 \pi}{5})=\sin ^{-1} \sin (\pi-\frac{2 \pi}{5})$

$ =\sin ^{-1} \sin (\frac{2 \pi}{5})=\frac{2 \pi}{5} \in[\frac{-\pi}{2}, \frac{\pi}{2}] $

Hence, the value of $\sin ^{-1}(\sin \frac{3 \pi}{5})=\frac{2 \pi}{5}$

Solution

Given that

$ \begin{aligned} & \cos [\tan ^{-1} x+\cot ^{-1} \sqrt{3}]=0 \\ \Rightarrow & \tan ^{-1} x+\cot ^{-1} \sqrt{3}=\cos ^{-1}(0) \\ \Rightarrow & \tan ^{-1} x+\cot ^{-1} \sqrt{3}=\frac{\pi}{2} \\ \Rightarrow & \tan ^{-1} x=\frac{\pi}{2}-\cot ^{-1} \sqrt{3} \\ \Rightarrow & \tan ^{-1} x=\tan ^{-1} \sqrt{3} \Rightarrow x=\sqrt{3} \end{aligned} \quad[\because \tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}] $

Hence, the value of $x$ is $\sqrt{3}$.

Solution

Let $\sec ^{-1}(\frac{1}{2})=x \Rightarrow \sec x=\frac{1}{2}$

Since, the domain of $\sec ^{-1} x$ is $R-{-1,1}$ and $\frac{1}{2} \notin R-{-1,1}$.

Hence, $\sec ^{-1}(\frac{1}{2})$ has no set of values.

Solution

$\tan ^{-1} \sqrt{3}=\tan ^{-1}(\tan \frac{\pi}{3})=\frac{\pi}{3} \in(\frac{-\pi}{2}, \frac{\pi}{2})$

Hence the principal value of $\tan ^{-1} \sqrt{3}$ is $\frac{\pi}{3}$.

Solution

$\quad \cos ^{-1}(\cos \frac{14 \pi}{3})=\cos ^{-1}[\cos (5 \pi-\frac{\pi}{3})]$

$ \begin{aligned} & =\cos ^{-1}[\cos (\frac{-\pi}{3})]=\cos ^{-1}[\cos (\pi-\frac{\pi}{3})] \\ & =\cos ^{-1}[\cos \frac{2 \pi}{3}]=\frac{2 \pi}{3} \in[0, \pi] \end{aligned} $

Hence, the value of $\cos ^{-1}[\cos \frac{14 \pi}{3}]=\frac{2 \pi}{3}$.

Solution

$\cos [\sin ^{-1} x+\cos ^{-1} x]=\cos \frac{\pi}{2}=0 \quad[\because \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}]$ Hence, the value of $\cos (\sin ^{-1} x+\cos ^{-1} x)=0$.

Solution

$\tan (\frac{\sin ^{-1} x+\cos ^{-1} x}{2})=\tan (\frac{\pi}{4})=1[\because \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}]$ Hence, the value of the given expression is 1 .

Solution

$ y=2 \tan ^{-1} x+\sin ^{-1}(\frac{2 x}{1+x^{2}}) $

$\begin{matrix} \Rightarrow & y=2 \tan ^{-1} x+2 \tan ^{-1} x \\ \Rightarrow & y=4 \tan ^{-1} x\end{matrix} [\because \sin ^{-1}(\frac{2 x}{1+x^{2}})=2 \tan ^{-1} x]$

Now $\frac{-\pi}{2}<\tan ^{-1} x<\frac{\pi}{2}$

$\Rightarrow \quad-4 \times \frac{\pi}{2}<4 \tan ^{-1} x<4 \times \frac{\pi}{2} \Rightarrow-2 \pi<y<2 \pi$

Hence, the value of $y$ is $(-2 \pi, 2 \pi)$.

Solution

The given result is true when $x y>-1$.

Solution

$\cot ^{-1}(-x)=\pi-\cot ^{-1} x, x \in R \quad[\because as^{-1}(-x)=\pi-\cot ^{-1} x]$

Solution

False.

We know that all inverse trigonometric functions are restricted over their domains.

Solution

False.

We know that $\cos ^{-1} x=\sec ^{-1}(\frac{1}{x}) \neq \sec x$ So

$ (\cos ^{-1} x)^{2} \neq \sec ^{2} x $

Solution

True.

We know that all trigonometric functions are restricted over their domains to obtain their inverse functions.

Solution

True.

Solution

True.

We know that the domain and range are interchanged in the graph of inverse trigonometric functions to that of their corresponding trigonometric functions.

Solution

False.

Given that $\tan ^{-1} \frac{n}{\pi}>\frac{\pi}{4}$

$ \begin{matrix} \Rightarrow & \frac{n}{\pi}>\tan \frac{\pi}{4} \Rightarrow \frac{n}{\pi}>1 \\ \Rightarrow & n>\pi \Rightarrow n>3.14 \end{matrix} $

Hence, the value of $n$ is 4 .

Solution

True.

$ \begin{aligned} \sin ^{-1}[\cos (\sin ^{-1} \frac{1}{2})] & =\sin ^{-1}[\cos (\sin ^{-1} \sin \frac{\pi}{6})] \\ \sin ^{-1}[\cos \frac{\pi}{6}] & =\sin ^{-1}(\frac{\sqrt{3}}{2})=\sin ^{-1}(\sin \frac{\pi}{3})=\frac{\pi}{3} \end{aligned} $