In most sciences one generation tears down what another has built and what one has established another undoes. In Mathematics alone each generation builds a new story to the old structure. - HERMAN HANKEL

10.1 Introduction

In our day to day life, we come across many queries such as - What is your height? How should a football player hit the ball to give a pass to another player of his team? Observe that a possible answer to the first query may be 1.6 meters, a quantity that involves only one value (magnitude) which is a real number. Such quantities are called scalars. However, an answer to the second query is a quantity (called force) which involves muscular strength (magnitude) and direction (in which another player is positioned). Such quantities are called vectors. In mathematics, physics and engineering, we frequently come across with both types of quantities, namely, scalar quantities such as length, mass, time, distance, speed, area, volume, temperature, work,money, voltage, density, resistance etc. and vector quantities like displacement, velocity, acceleration, force, weight, momentum, electric field intensity etc.

W.R. Hamilton $(1805-1865)$

In this chapter, we will study some of the basic concepts about vectors, various operations on vectors, and their algebraic and geometric properties. These two type of properties, when considered together give a full realisation to the concept of vectors, and lead to their vital applicability in various areas as mentioned above.

10.2 Some Basic Concepts

Let ’ $l$ ’ be any straight line in plane or three dimensional space. This line can be given two directions by means of arrowheads. A line with one of these directions prescribed is called a directed line (Fig 10.1 (i), (ii)).

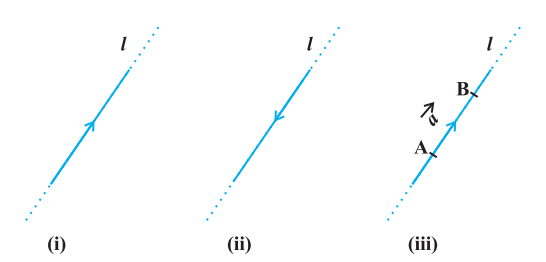
Fig 10.1

Now observe that if we restrict the line $l$ to the line segment AB, then a magnitude is prescribed on the line $l$ with one of the two directions, so that we obtain a directed line segment (Fig 10.1(iii)). Thus, a directed line segment has magnitude as well as direction.

Definition 1 A quantity that has magnitude as well as direction is called a vector.

Notice that a directed line segment is a vector (Fig 10.1(iii)), denoted as $\overrightarrow{{}AB}$ or simply as $\vec{a}$, and read as ‘vector $\overrightarrow{{}AB}$ ’ or ‘vector $\vec{a}$ ‘.

The point $A$ from where the vector $\overrightarrow{{}AB}$ starts is called its initial point, and the point $B$ where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as $|\overrightarrow{{}AB}|$, or $|\vec{a}|$, or $a$. The arrow indicates the direction of the vector.

Note Since the length is never negative, the notation $|\vec{a}|<0$ has no meaning.

Position Vector

From Class XI, recall the three dimensional right handed rectangular coordinate system (Fig 10.2(i)). Consider a point $P$ in space, having coordinates $(x, y, z)$ with respect to the origin $O(0,0,0)$. Then, the vector $\overrightarrow{{}OP}$ having $O$ and $P$ as its initial and terminal points, respectively, is called the position vector of the point $P$ with respect to $O$. Using distance formula (from Class XI), the magnitude of $\overrightarrow{{}OP}$ (or $\vec{r}$ ) is given by

$$ |\overrightarrow{{}OP}|=\sqrt{x^{2}+y^{2}+z^{2}} $$

In practice, the position vectors of points $A, B, C$, etc., with respect to the origin $O$ are denoted by $\vec{a}, \vec{b}, \vec{c}$, etc., respectively (Fig 10.2 (ii)).

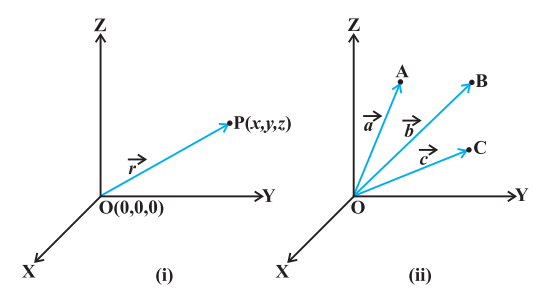
Fig 10.2

Direction Cosines

Consider the position vector $\overrightarrow{{}OP}$ (or $\vec{r}$ ) of a point $P(x, y, z)$ as in Fig 10.3. The angles $\alpha$, $\beta, \gamma$ made by the vector $\vec{r}$ with the positive directions of $x, y$ and $z$-axes respectively, are called its direction angles. The cosine values of these angles, i.e., $\cos \alpha, \cos \beta$ and $\cos \gamma$ are called direction cosines of the vector $\vec{r}$, and usually denoted by $l, m$ and $n$, respectively.

From Fig 10.3, one may note that the triangle OAP is right angled, and in it, we have $\cos \alpha=\frac{x}{r}(r$ stands for $|\vec{r}|)$. Similarly, from the right angled triangles OBP and OCP, we may write $\cos \beta=\frac{y}{r}$ and $\cos \gamma=\frac{z}{r}$. Thus, the coordinates of the point P may also be expressed as $(l r, m r, n r)$. The numbers $l r, m r$ and $n r$, proportional to the direction cosines are called as direction ratios of vector $\vec{r}$, and denoted as $a, b$ and $c$, respectively.

Note One may note that $l^{2}+m^{2}+n^{2}=1$ but $a^{2}+b^{2}+c^{2} \neq 1$, in general.

10.3 Types of Vectors

Zero Vector A vector whose initial and terminal points coincide, is called a zero vector (or null vector), and denoted as $\overrightarrow{{}0}$. Zero vector can not be assigned a definite direction as it has zero magnitude. Or, alternatively otherwise, it may be regarded as having any direction. The vectors $\overrightarrow{{}AA}, \overrightarrow{{}BB}$ represent the zero vector,

Unit Vector A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The unit vector in the direction of a given vector $\vec{a}$ is denoted by $\hat{a}$.Coinitial Vectors Two or more vectors having the same initial point are called coinitial vectors.

Collinear Vectors Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.

Equal Vectors Two vectors $\vec{a}$ and $\vec{b}$ are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written as $\vec{a}=\vec{b}$.

Negative of a Vector A vector whose magnitude is the same as that of a given vector (say, $\overrightarrow{{}AB}$ ), but direction is opposite to that of it, is called negative of the given vector. For example, vector $\overrightarrow{{}BA}$ is negative of the vector $\overrightarrow{{}AB}$, and written as $\overrightarrow{{}BA}=-\overrightarrow{{}AB}$.

Remark The vectors defined above are such that any of them may be subject to its parallel displacement without changing its magnitude and direction. Such vectors are called free vectors. Throughout this chapter, we will be dealing with free vectors only.

Example 1 Represent graphically a displacement of $40 km, 30^{\circ}$ west of south.

Solution The vector $\overrightarrow{{}OP}$ represents the required displacement (Fig 10.4).

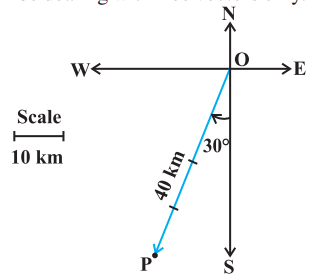
Fig 10.4

Example 2 Classify the following measures as scalars and vectors.

(i) $5 \mathrm{~s}$

(ii) $1000 \mathrm{~cm}^{3}$

(iii) $10 \mathrm{~N}$

(iv) $30 \mathrm{~km} / \mathrm{h}$

(v) $10 \mathrm{~g} / \mathrm{cm}^{3}$

(vi) $20 m / s$ towards north

Solution

(i) Time-scalar

(ii) Volume-scalar

(iii) Force-vector

(iv) Speed-scalar

(v) Density-scalar

(vi) Velocity-vector

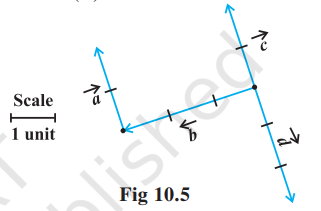
Example 3 In Fig 10.5, which of the vectors are:

(i) Collinear

(ii) Equal

(iii) Coinitial

Solution

(i) Collinear vectors: $\vec{a}, \vec{c}$ and $\vec{d}$.

(ii) Equal vectors : $\vec{a}$ and $\vec{c}$.

(iii) Coinitial vectors : $\vec{b}, \vec{c}$ and $\vec{d}$.

EXERCISE 10.1

1. Represent graphically a displacement of $40 km, 30^{\circ}$ east of north.

Show Answer

Solution

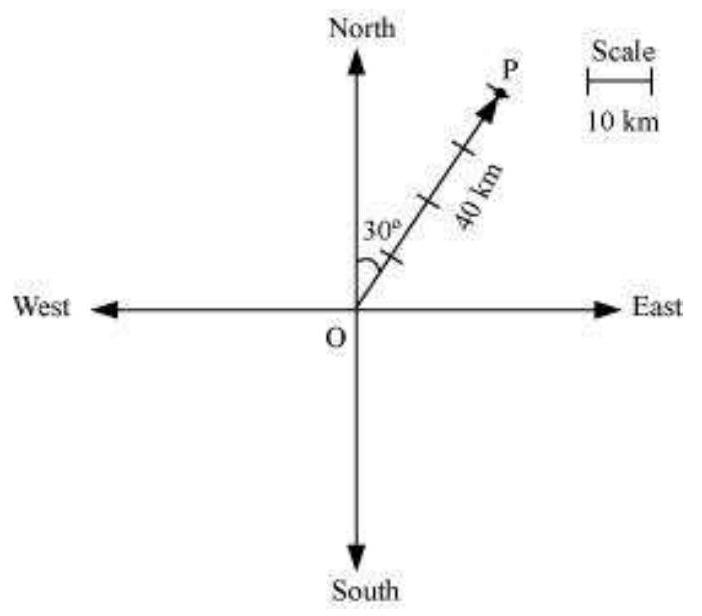
Here, vector $\overrightarrow{{}OP}$ represents the displacement of $40 km, 30^{\circ}$ East of North.

2. Classify the following measures as scalars and vectors.

(i) $10 kg$

(ii) 2 meters north-west

(iii) $40^{\circ}$

(iv) 40 watt

(v) $10^{-19}$ coulomb

(vi) $20 m / s^{2}$

Show Answer

Solution

(i) $10 kg$ is a scalar quantity because it involves only magnitude.

(ii) 2 meters north-west is a vector quantity as it involves both magnitude and direction.

(iii) $40^{\circ}$ is a scalar quantity as it involves only magnitude.

(iv) 40 watts is a scalar quantity as it involves only magnitude.

(v) $10^{-19}$ coulomb is a scalar quantity as it involves only magnitude.

(vi) $20 m / s^{2}$ is a vector quantity as it involves magnitude as well as direction.

3. Classify the following as scalar and vector quantities.

(i) time period

(ii) distance

(iv) velocity

(v) work done

(iii) force

Show Answer

Solution

(i) Time period is a scalar quantity as it involves only magnitude.

(ii) Distance is a scalar quantity as it involves only magnitude.

(iii) Force is a vector quantity as it involves both magnitude and direction.

(iv) Velocity is a vector quantity as it involves both magnitude as well as direction.

(v) Work done is a scalar quantity as it involves only magnitude.

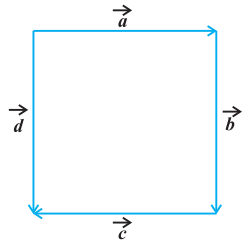
4. In Fig 10.6 (a square), identify the following vectors.

(i) Coinitial

(ii) Equal

(iii) Collinear but not equal

Show Answer

Solution

(i) Vectors $\vec{a}$ and $\vec{d}$ are coinitial because they have the same initial point.

(ii) Vectors $\vec{b}$ and $\vec{d}$ are equal because they have the same magnitude and direction.

(iii) Vectors $\vec{a}$ and $\vec{c}$ are collinear but not equal. This is because although they are parallel, their directions are not the same.

5. Answer the following as true or false.

(i) $\vec{a}$ and $-\vec{a}$ are collinear.

(ii) Two collinear vectors are always equal in magnitude.

(iii) Two vectors having same magnitude are collinear.

Fig 10.6

(iv) Two collinear vectors having the same magnitude are equal.

Show Answer

Solution

(i) True.

Vectors $\vec{a}$ and $-\vec{a}$ are parallel to the same line.

(ii) False.

Collinear vectors are those vectors that are parallel to the same line.

(iii) False.

10.4 Addition of Vectors

A vector $\overrightarrow{{}AB}$ simply means the displacement from a point A to the point $B$. Now consider a situation that a girl moves from $A$ to $B$ and then from $B$ to $C$ (Fig 10.7). The net displacement made by the girl from point $A$ to the point $C$, is given by the vector $\overrightarrow{{}AC}$ and expressed as

Fig 10.7

$ \overrightarrow{{}AC}=\overrightarrow{{}AB}+\overrightarrow{{}BC} $

This is known as the triangle law of vector addition.

In general, if we have two vectors $\vec{a}$ and $\vec{b}$ (Fig 10.8 (i)), then to add them, they are positioned so that the initial point of one coincides with the terminal point of the other (Fig 10.8(ii)).

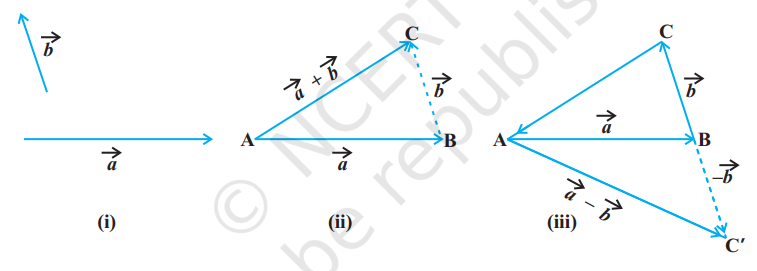
Fig 10.8

For example, in Fig 10.8 (ii), we have shifted vector $\vec{b}$ without changing its magnitude and direction, so that it’s initial point coincides with the terminal point of $\vec{a}$. Then, the vector $\vec{a}+\vec{b}$, represented by the third side $AC$ of the triangle $ABC$, gives us the sum (or resultant) of the vectors $\vec{a}$ and $\vec{b}$ i.e., in triangle $ABC$ (Fig 10.8 (ii)), we have

$ \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC} $

Now again, since $\overrightarrow{{}AC}=-\overrightarrow{{}CA}$, from the above equation, we have

$$ \overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}AA}=\overrightarrow{{}0} $$

This means that when the sides of a triangle are taken in order, it leads to zero resultant as the initial and terminal points get coincided (Fig 10.8(iii)).

Now, construct a vector $\overrightarrow{{}BC^{\prime}}$ so that its magnitude is same as the vector $\overrightarrow{{}BC}$, but the direction opposite to that of it (Fig 10.8 (iii)), i.e., $ \overrightarrow{{}BC^{\prime}}=-\overrightarrow{{}BC} $ Then, on applying triangle law from the Fig 10.8 (iii), we have $ \overrightarrow{{}AC^{\prime}}=\overrightarrow{{}AB}+\overrightarrow{{}BC^{\prime}}=\overrightarrow{{}AB}+(-\overrightarrow{{}BC})=\vec{a}-\vec{b} $

The vector $\overrightarrow{{}AC^{\prime}}$ is said to represent the difference of $\vec{a}$ and $\vec{b}$.

Now, consider a boat in a river going from one bank of the river to the other in a direction perpendicular to the flow of the river. Then, it is acted upon by two velocity vectors-one is the velocity imparted to the boat by its engine and other one is the velocity of the flow of river water. Under the simultaneous influence of these two velocities, the boat in actual starts travelling with a different velocity. To have a precise idea about the effective speed and direction (i.e., the resultant velocity) of the boat, we have the following law of vector addition.

If we have two vectors $\vec{a}$ and $\vec{b}$ represented by the two adjacent sides of a parallelogram in magnitude and direction (Fig 10.9), then their sum $\vec{a}+\vec{b}$ is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.

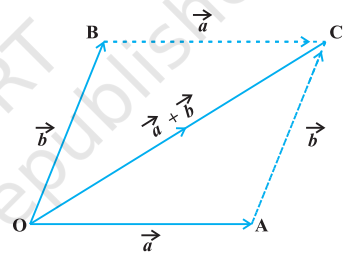
Fig 10.9

Note From Fig 10.9, using the triangle law, one may note that

$\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OC}}$ or $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}$ (since $\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OB}}$ )

which is parallelogram law. Thus, we may say that the two laws of vector addition are equivalent to each other.

Properties of vector addition

Property 1 For any two vectors $\vec{a}$ and $\vec{b}$,

$ \vec{a}+\vec{b}=\vec{b}+\vec{a} $

(Commutative property) Proof Consider the parallelogram $ABCD$ (Fig 10.10). Let $\overrightarrow{{}AB}=\vec{a}$ and $\overrightarrow{{}BC}=\vec{b}$, then using the triangle law, from triangle $ABC$, we have $ \overrightarrow{{}AC}=\vec{a}+\vec{b} $

Now, since the opposite sides of a parallelogram are equal and parallel, from Fig 10.10, we have, $\overrightarrow{{}AD}=\overrightarrow{{}BC}=\vec{b}$ and $\overrightarrow{{}DC}=\overrightarrow{{}AB}=\vec{a}$. Again using triangle law, from

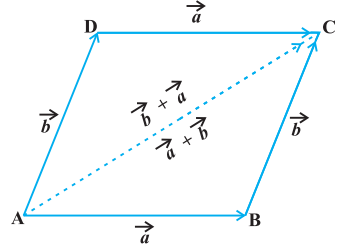
Fig 10.10 triangle $ADC$, we have

$ \overrightarrow{{}AC}=\overrightarrow{{}AD}+\overrightarrow{{}DC}=\vec{b}+\vec{a} $

Hence

$ \vec{a}+\vec{b}=\vec{b}+\vec{a} $

Property 2 For any three vectors $a, b$ and $c$

$ (\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) $

Proof Let the vectors $\vec{a}, \vec{b}$ and $\vec{c}$ be represented by $\overrightarrow{{}PQ}, \overrightarrow{{}QR}$ and $\overrightarrow{{}RS}$, respectively, as shown in Fig 10.11(i) and (ii).

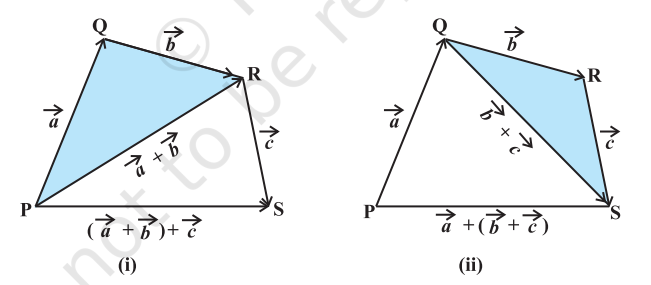
Fig 10.11

Then $$\quad\quad\vec{a}+\vec{b}=\overrightarrow{{}PQ}+\overrightarrow{{}QR}=\overrightarrow{{}PR}$$

and $$ \quad\quad\vec{b}+\vec{c}=\overrightarrow{{}QR}+\overrightarrow{{}RS}=\overrightarrow{{}QS}$$

So $$ \quad\quad(\vec{a}+\vec{b})+\vec{c}=\overrightarrow{{}PR}+\overrightarrow{{}RS}=\overrightarrow{{}PS}$$

and $$\quad \quad\vec{a}+(\vec{b}+\vec{c})=\overrightarrow{{}PQ}+\overrightarrow{{}QS}=\overrightarrow{{}PS}$$

Hence $$\quad(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$$

Remark The associative property of vector addition enables us to write the sum of three vectors $\vec{a}, \vec{b}, \vec{c}$ as $\vec{a}+\vec{b}+\vec{c}$ without using brackets.

Note that for any vector $a$, we have

$$ \vec{a}+\overrightarrow{{}0}=\overrightarrow{{}0}+\vec{a}=\vec{a} $$

Here, the zero vector $\overrightarrow{{}0}$ is called the additive identity for the vector addition.

10.5 Multiplication of a Vector by a Scalar

Let $\vec{a}$ be a given vector and $\lambda$ a scalar. Then the product of the vector $\vec{a}$ by the scalar $\lambda$, denoted as $\lambda \vec{a}$, is called the multiplication of vector $\vec{a}$ by the scalar $\lambda$. Note that, $\lambda \vec{a}$ is also a vector, collinear to the vector $\vec{a}$. The vector $\lambda \vec{a}$ has the direction same (or opposite) to that of vector $\vec{a}$ according as the value of $\lambda$ is positive (or negative). Also, the magnitude of vector $\lambda \vec{a}$ is $|\lambda|$ times the magnitude of the vector $\vec{a}$, i.e.,

$$ |\lambda \vec{a}|=|\lambda||\vec{a}| $$

A geometric visualisation of multiplication of a vector by a scalar is given in Fig 10.12.

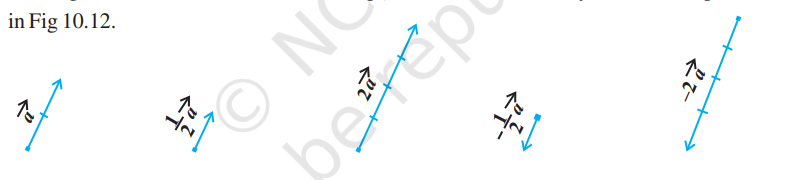
Fig 10.12

When $\lambda=-1$, then $\lambda \vec{a}=-\vec{a}$, which is a vector having magnitude equal to the magnitude of $\vec{a}$ and direction opposite to that of the direction of $\vec{a}$. The vector $-\vec{a}$ is called the negative (or additive inverse) of vector $\vec{a}$ and we always have

$ \vec{a}+(-\vec{a})=(-\vec{a})+\vec{a}=\overrightarrow{{}0} $

Also, if $\lambda=\frac{1}{|a|}$, provided $\vec{a} \neq 0$ i.e. $\vec{a}$ is not a null vector,

then $$ |\lambda \vec{a}|=|\lambda||\vec{a}|=\frac{1}{|\vec{a}|}|\vec{a}|=1 $$

So, $\lambda \vec{a}$ represents the unit vector in the direction of $\vec{a}$. We write it as

$$ \hat{a}=\frac{1}{|\vec{a}|} \vec{a} $$

Note For any scalar $k, k \overrightarrow{{}0}=\overrightarrow{{}0}$.

10.5.1 Components of a vector

Let us take the points $A(1,0,0), B(0,1,0)$ and $C(0,0,1)$ on the $x$-axis, $y$-axis and $z$-axis, respectively. Then, clearly

$$ |\overrightarrow{{}OA}|=1,|\overrightarrow{{}OB}|=1 \text{ and }|\overrightarrow{{}OC}|=1 $$

The vectors $\overrightarrow{{}OA}, \overrightarrow{{}OB}$ and $\overrightarrow{{}OC}$, each having magnitude 1 , are called unit vectors along the axes $OX, OY$ and $OZ$, respectively, and denoted by $\hat{i}, \hat{j}$ and $\hat{k}$, respectively (Fig 10.13).

Now, consider the position vector $\overline{OP}$ of a point $P(x, y, z)$ Fig 10.13 as in Fig 10.14. Let $P_1$ be the foot of the perpendicular from $P$ on the plane XOY. We, thus, see that $P_1 P$ is parallel to $z$-axis. As $\hat{i}, \hat{j}$ and $\hat{k}$ are the unit vectors along the $x, y$ and $z$-axes, respectively, and by the definition of the coordinates of $P$, we have $\overrightarrow{{}P_1 P}=\overrightarrow{{}OR}=z \hat{k}$. Similarly, $\overrightarrow{{}QP_1}=\overrightarrow{{}OS}=y \hat{j}$ and $\overrightarrow{{}OQ}=x \hat{i}$.

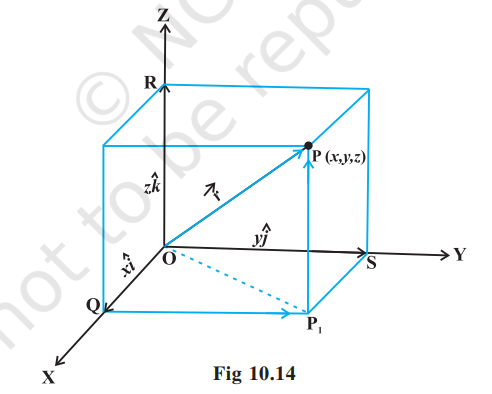
Therefore, it follows that

$$ \begin{aligned} & \overrightarrow{{}OP_1}=\overrightarrow{{}OQ}+\overrightarrow{{}QP_1}=x \hat{i}+y \hat{j} \\ & \overrightarrow{{}OP}=\overrightarrow{{}OP_1}+\overrightarrow{{}P_1 P}=x \hat{i}+y \hat{j}+z \hat{k} \end{aligned} $$

Hence, the position vector of $P$ with reference to $O$ is given by

$ \overrightarrow{{}OP}(\text{ or } \vec{r})=x \hat{i}+y \hat{j}+z \hat{k} $

This form of any vector is called its component form. Here, $x, y$ and $z$ are called as the scalar components of $\vec{r}$, and $x \hat{i}, y \hat{j}$ and $z \hat{k}$ are called the vector components of $\vec{r}$ along the respective axes. Sometimes $x, y$ and $z$ are also termed as rectangular components.

The length of any vector $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$, is readily determined by applying the Pythagoras theorem twice. We note that in the right angle triangle OQP (Fig 10.14) $^{\text{(F) }}$

$$ |\overrightarrow{{}OP_1}|=\sqrt{|\overrightarrow{{}OQ}|^{2}+|\overrightarrow{{}QP_1}|^{2}}=\sqrt{x^{2}+y^{2}}, $$

and in the right angle triangle $OP_1 P$, we have

$$ \overrightarrow{{}OP}=\sqrt{|\overrightarrow{{}OP_1}|^{2}+|\overrightarrow{{}P_1 P}|^{2}}=\sqrt{(x^{2}+y^{2})+z^{2}} $$

Hence, the length of any vector $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ is given by $$ |\vec{r}|=|x \hat{i}+y \hat{j}+z \hat{k}|=\sqrt{x^{2}+y^{2}+z^{2}} $$

If $\vec{a}$ and $\vec{b}$ are any two vectors given in the component form $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, respectively, then

(i) the sum (or resultant) of the vectors $\vec{a}$ and $\vec{b}$ is given by

$$ \vec{a}+\vec{b}=(a_1+b_1) \hat{i}+(a_2+b_2) \hat{j}+(a_3+b_3) \hat{k} $$

(ii) the difference of the vector $\vec{a}$ and $\vec{b}$ is given by

$$ \vec{a}-\vec{b}=(a_1-b_1) \hat{i}+(a_2-b_2) \hat{j}+(a_3-b_3) \hat{k} $$

(iii) the vectors $\vec{a}$ and $\vec{b}$ are equal if and only if

$$ a_1=b_1, a_2=b_2 \quad \text{ and } \quad a_3=b_3 $$

(iv) the multiplication of vector $\vec{a}$ by any scalar $\lambda$ is given by

$$ \lambda \vec{a}=(\lambda a_1) \hat{i}+(\lambda a_2) \hat{j}+(\lambda a_3) \hat{k} $$

The addition of vectors and the multiplication of a vector by a scalar together give the following distributive laws:

Let $\vec{a}$ and $\vec{b}$ be any two vectors, and $k$ and $m$ be any scalars. Then

(i) $k \vec{a}+m \vec{a}=(k+m) \vec{a}$

(ii) $k(m \vec{a})=(k m) \vec{a}$

(iii) $k(\vec{a}+\vec{b})=k \vec{a}+k \vec{b}$

Remarks

(i) One may observe that whatever be the value of $\lambda$, the vector $\lambda \vec{a}$ is always collinear to the vector $\vec{a}$. In fact, two vectors $\vec{a}$ and $\vec{b}$ are collinear if and only if there exists a nonzero scalar $\lambda$ such that $\vec{b}=\lambda \vec{a}$. If the vectors $\vec{a}$ and $\vec{b}$ are given in the component form, i.e. $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, then the two vectors are collinear if and only if

$$ \begin{array}{cc} & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda\left(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\right) \\ \Leftrightarrow & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\left(\lambda a_1\right) \hat{i}+\left(\lambda a_2\right) \hat{j}+\left(\lambda a_3\right) \hat{k} \\ \Leftrightarrow & b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3 \\ \Leftrightarrow & \frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}=\lambda \end{array} $$

(ii) If $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$, then $a_1, a_2, a_3$ are also called direction ratios of $\vec{a}$.

(iii) In case if it is given that $l, m, n$ are direction cosines of a vector, then $l \hat{i}+m \hat{j}+n \hat{k}$ $=(\cos \alpha) \hat{i}+(\cos \beta) \hat{j}+(\cos \gamma) \hat{k}$ is the unit vector in the direction of that vector, where $\alpha, \beta$ and $\gamma$ are the angles which the vector makes with $x, y$ and $z$ axes respectively.

Example 4 Find the values of $x, y$ and $z$ so that the vectors $\vec{a}=x \hat{i}+2 \hat{j}+z \hat{k}$ and $\vec{b}=2 \hat{i}+y \hat{j}+\hat{k}$ are equal.

Solution Note that two vectors are equal if and only if their corresponding components are equal. Thus, the given vectors $\vec{a}$ and $\vec{b}$ will be equal if and only if $ x=2, y=2, z=1 $

Example 5 Let $\vec{a}=\hat{i}+2 \hat{j}$ and $\vec{b}=2 \hat{i}+\hat{j}$. Is $|\vec{a}|=|\vec{b}|$ ? Are the vectors $\vec{a}$ and $\vec{b}$ equal?

Solution We have $|\vec{a}|=\sqrt{1^{2}+2^{2}}=\sqrt{5}$ and $|\vec{b}|=\sqrt{2^{2}+1^{2}}=\sqrt{5}$

So, $|\vec{a}|=|\vec{b}|$. But, the two vectors are not equal since their corresponding components are distinct.

Example 6 Find unit vector in the direction of vector $\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}$

Solution The unit vector in the direction of a vector $\vec{a}$ is given by $\hat{a}=\frac{1}{|\vec{a}|} \vec{a}$.

Now $ |\vec{a}|=\sqrt{2^{2}+3^{2}+1^{2}}=\sqrt{14} $

Therefore $ \hat{a}=\frac{1}{\sqrt{14}}(2 \hat{i}+3 \hat{j}+\hat{k})=\frac{2}{\sqrt{14}} \hat{i}+\frac{3}{\sqrt{14}} \hat{j}+\frac{1}{\sqrt{14}} \hat{k} $

Example 7 Find a vector in the direction of vector $\vec{a}=\hat{i}-2 \hat{j}$ that has magnitude 7 units.

Solution The unit vector in the direction of the given vector $\vec{a}$ is $ \hat{a}=\frac{1}{|\vec{a}|} \vec{a}=\frac{1}{\sqrt{5}}(\hat{i}-2 \hat{j})=\frac{1}{\sqrt{5}} \hat{i}-\frac{2}{\sqrt{5}} \hat{j} $ Therefore, the vector having magnitude equal to 7 and in the direction of $\vec{a}$ is $ 7 \hat{a}=7(\frac{1}{\sqrt{5}} \hat{i}-\frac{2}{\sqrt{5}} \hat{j})=\frac{7}{\sqrt{5}} \hat{i}-\frac{14}{\sqrt{5}} \hat{j} $

Example 8 Find the unit vector in the direction of the sum of the vectors, $\vec{a}=2 \hat{i}+2 \hat{j}-5 \hat{k}$ and $\vec{b}=2 \hat{i}+\hat{j}+3 \hat{k}$.

Solution The sum of the given vectors is

$ \begin{aligned} & \vec{a}+\vec{b}(=\vec{c}, \text{ say })=4 \hat{i}+3 \hat{j}-2 \hat{k} \\ \text {and } \qquad & \quad|\vec{c}|=\sqrt{4^{2}+3^{2}+(-2)^{2}}=\sqrt{29} \end{aligned} $

Thus, the required unit vector is

$$ \hat{c}=\frac{1}{|\vec{c}|} \vec{c}=\frac{1}{\sqrt{29}}(4 \hat{i}+3 \hat{j}-2 \hat{k})=\frac{4}{\sqrt{29}} \hat{i}+\frac{3}{\sqrt{29}} \hat{j}-\frac{2}{\sqrt{29}} \hat{k} $$

Example 9 Write the direction ratio’s of the vector $\vec{a}=\hat{i}+\hat{j}-2 \hat{k}$ and hence calculate its direction cosines.

Solution Note that the direction ratio’s $a, b, c$ of a vector $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ are just the respective components $x, y$ and $z$ of the vector. So, for the given vector, we have $a=1, b=1$ and $c=-2$. Further, if $l, m$ and $n$ are the direction cosines of the given vector, then

$$ 1=\frac{a}{|\vec{r}|}=\frac{1}{\sqrt{6}}, \quad m=\frac{b}{|\vec{r}|}=\frac{1}{\sqrt{6}}, \quad n=\frac{c}{|\vec{r}|}=\frac{-2}{\sqrt{6}} \text{ as }|\vec{r}|=\sqrt{6} $$

Thus, the direction cosines are $(\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}})$.

10.5.2 Vector joining two points

If $P_1(x_1, y_1, z_1)$ and $P_2(x_2, y_2, z_2)$ are any two points, then the vector joining $P_1$ and $P_2$ is the vector $\overrightarrow{{}P_1} _2$ (Fig 10.15). Joining the points $P_1$ and $P_2$ with the origin $O$, and applying triangle law, from the triangle $OP_1 P_2$, we have $ \overrightarrow{{}OP_1}+\overrightarrow{{}P_1} _2=\overrightarrow{{}OP_2} $

Using the properties of vector addition, the above equation becomes

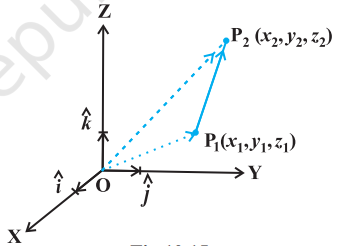
Fig 10.15

$$ \text{ i.e. } \quad \begin{aligned} \overrightarrow{{}P_1} _2 & =\overrightarrow{{}OP_2}-\overrightarrow{{}OP_1} \\ \overrightarrow{{}P_1} _2 & =(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k})-(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}) \\ & =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} \end{aligned} $$

The magnitude of vector $\overrightarrow{{}P_1} _2$ is given by $$ |\overrightarrow{{}P_1} _2|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $$

Example 10 Find the vector joining the points $P(2,3,0)$ and $Q(-1,-2,-4)$ directed from $P$ to $Q$.

Solution Since the vector is to be directed from P to Q, clearly P is the initial point and $Q$ is the terminal point. So, the required vector joining $P$ and $Q$ is the vector $\overrightarrow{{}PQ}$, given by

$$ \begin{aligned} & \overrightarrow{{}PQ}=(-1-2) \hat{i}+(-2-3) \hat{j}+(-4-0) \hat{k} \\ \text { i.e. } \qquad & \overrightarrow{{}PQ}=-3 \hat{i}-5 \hat{j}-4 \hat{k} \end{aligned} $$

10.5.3 Section formula

Let $P$ and $Q$ be two points represented by the position vectors $\overrightarrow{{}OP}$ and $\overrightarrow{{}OQ}$, respectively, with respect to the origin $O$. Then the line segment joining the points $P$ and $Q$ may be divided by a third point, say R, in two ways - internally (Fig 10.16) and externally (Fig 10.17). Here, we intend to find the position vector $\overrightarrow{{}OR}$ for the point $R$ with respect to the origin $O$. We take the two cases one by one.

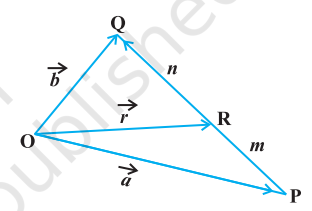
Fig 10.16

Case II When R divides PQ internally (Fig 10.16). If $R$ divides $\overrightarrow{{}PQ}$ such that $m \overrightarrow{{}RQ}=n \overrightarrow{{}PR}$,

where $m$ and $n$ are positive scalars, we say that the point $R$ divides $\overrightarrow{{}PQ}$ internally in the ratio of $m: n$. Now from triangles ORQ and OPR, we have

$$ \overrightarrow{{}RQ}=\overrightarrow{{}OQ}-\overrightarrow{{}OR}=\vec{b}-\vec{r} $$

$$ \text { and } \qquad \overrightarrow{{}PR}=\overrightarrow{{}OR}-\overrightarrow{{}OP}=\vec{r}-\vec{a} $$

$$ \begin{aligned} \text { Therefore, we have } \qquad m(\vec{b}-\vec{r}) & =n(\vec{r}-\vec{a}) \quad \text{ (Why?) } \end{aligned} $$

$$ \begin{aligned} \text {or } \qquad \vec{r} & =\frac{m \vec{b}+n \vec{a}}{m+n} \qquad \text{ (on simplification) } \end{aligned} $$

Hence, the position vector of the point $R$ which divides $P$ and $Q$ internally in the ratio of $m: n$ is given by

$$ \overrightarrow{{}OR}=\frac{m \vec{b}+n \vec{a}}{m+n} $$

Case II When R divides PQ externally (Fig 10.17). We leave it to the reader as an exercise to verify that the position vector of the point $R$ which divides the line segment $P Q$ externally in the ratio $m: n$ i.e. $\frac{PR}{QR}=\frac{m}{n}$ is given by $ \overrightarrow{{}OR}=\frac{m \vec{b}-n \vec{a}}{m-n} $

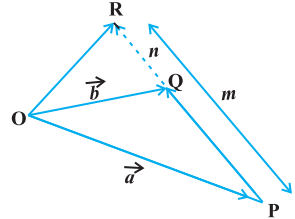
Fig 10.17

Remark If $R$ is the midpoint of $PQ$, then $m=n$. And therefore, from Case I, the midpoint $R$ of $\overrightarrow{{}PQ}$, will have its position vector as $ \overrightarrow{{}OR}=\frac{\vec{a}+\vec{b}}{2} $

Example 11 Consider two points $P$ and $Q$ with position vectors $\overrightarrow{{}OP}=3 \vec{a}-2 \vec{b}$ and $\overrightarrow{{}OQ}=\vec{a}+\vec{b}$. Find the position vector of a point $R$ which divides the line joining $P$ and $Q$ in the ratio $2: 1$, (i) internally, and (ii) externally.

Solution

(i) The position vector of the point $R$ dividing the join of $P$ and $Q$ internally in the ratio $2: 1$ is

$$ \overrightarrow{{}OR}=\frac{2(\vec{a}+\vec{b})+(3 \vec{a}-2 \vec{b})}{2+1}=\frac{5 \vec{a}}{3} $$

(ii) The position vector of the point $R$ dividing the join of $P$ and $Q$ externally in the ratio $2: 1$ is

$$ \overrightarrow{{}OR}=\frac{2(\vec{a}+\vec{b})-(3 \vec{a}-2 \vec{b})}{2-1}=4 \vec{b}-\vec{a} $$

Example 12 Show that the points $A(2 \hat{i}-\hat{j}+\hat{k}), B(\hat{i}-3 \hat{j}-5 \hat{k}), C(3 \hat{i}-4 j-4 \hat{k})$ are the vertices of a right angled triangle.

Solution We have

$$ \begin{aligned} & \overrightarrow{{}AB}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k} \\ & \overrightarrow{{}BC}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k} \end{aligned} $$

$$ \overrightarrow{{}CA}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k} $$

Further, note that

$$ |\overrightarrow{{}AB}|^{2}=41=6+35=|\overrightarrow{{}BC}|^{2}+|\overrightarrow{{}CA}|^{2} $$

Hence, the triangle is a right angled triangle.

EXERCISE 10.2

1. Compute the magnitude of the following vectors:

$$ \vec{a}=\hat{i}+\hat{j}+k ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k} $$

Show Answer

Solution

The given vectors are:

$ \begin{aligned} \vec{a} & =\hat{i}+\hat{j}+\hat{k} ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k} \\ |\vec{a}| & =\sqrt{(1)^{2}+(1)^{2}+(1)^{2}}=\sqrt{3} \\ |\vec{b}| & =\sqrt{(2)^{2}+(-7)^{2}+(-3)^{2}} \\ & =\sqrt{4+49+9} \\ & =\sqrt{62} \\ |\vec{c}| & =\sqrt{(\frac{1}{\sqrt{3}})^{2}+(\frac{1}{\sqrt{3}})^{2}+(-\frac{1}{\sqrt{3}})^{2}} \\ & =\sqrt{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}=1 \end{aligned} $

2. Write two different vectors having same magnitude.

Show Answer

Solution

Consider $\vec{a}=(\hat{i}-2 \hat{j}+3 \hat{k})$ and $\vec{b}=(2 \hat{i}+\hat{j}-3 \hat{k})$.

It can be observed that $|\vec{a}|=\sqrt{1^{2}+(-2)^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$ and $|\vec{b}|=\sqrt{2^{2}+1^{2}+(-3)^{2}}=\sqrt{4+1+9}=\sqrt{14}$.

Hence, $\vec{a}$ and $\vec{b}$ are two different vectors having the same magnitude. The vectors are different because they have different directions.

3. Write two different vectors having same direction.

Show Answer

Solution

Consider $\vec{p}=(\hat{i}+\hat{j}+\hat{k})$ and $\vec{q}=(2 \hat{i}+2 \hat{j}+2 \hat{k})$.

The direction cosines of $\vec{p}$ are given by,

$l=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}, m=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}$, and $n=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}$.

The direction cosines of $\vec{q}$ are given by

$l=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}, m=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}$,

and $n=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}$.

The direction cosines of $\vec{p}$ and $\vec{q}$ are the same. Hence, the two vectors have the same direction.

4. Find the values of $x$ and $y$ so that the vectors $2 \hat{i}+3 \hat{j}$ and $x \hat{i}+y \hat{j}$ are equal.

Show Answer

Solution

The two vectors $2 \hat{i}+3 \hat{j}$ and $x \hat{i}+y \hat{j}$ will be equal if their corresponding components are equal.

Hence, the required values of $x$ and $y$ are 2 and 3 respectively.

5. Find the scalar and vector components of the vector with initial point $(2,1)$ and terminal point $(-5,7)$.

Show Answer

Solution

The vector with the initial point $P(2,1)$ and terminal point $Q(-5,7)$ can be given by, $\overrightarrow{{}PQ}=(-5-2) \hat{i}+(7-1) \hat{j}$

$\Rightarrow \overrightarrow{{}PQ}=-7 \hat{i}+6 \hat{j}$

Hence, the required scalar components are -7 and 6 while the vector components are $-7 \hat{i}$ and $6 \hat{j}$.

6. Find the sum of the vectors $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ and $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$.

Show Answer

Solution

The given vectors are $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ and $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$.

$ \begin{aligned} \therefore \vec{a}+\vec{b}+\vec{c} & =(1-2+1) \hat{i}+(-2+4-6) \hat{j}+(1+5-7) \hat{k} \\ & =0 \cdot \hat{i}-4 \hat{j}-1 \cdot \hat{k} \\ & =-4 \hat{j}-\hat{k} \end{aligned} $

7. Find the unit vector in the direction of the vector $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$.

Show Answer

Solution

The unit vector $\hat{a}$ in the direction of vector $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$ is given by $\hat{a}=\frac{\vec{a}}{|a|}$.

$|\vec{a}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{1+1+4}=\sqrt{6}$

$\therefore \hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{\hat{i}+\hat{j}+2 \hat{k}}{\sqrt{6}}=\frac{1}{\sqrt{6}} \hat{i}+\frac{1}{\sqrt{6}} \hat{j}+\frac{2}{\sqrt{6}} \hat{k}$

8. Find the unit vector in the direction of vector $\overrightarrow{{}PQ}$, where $P$ and $Q$ are the points $(1,2,3)$ and $(4,5,6)$, respectively.

Show Answer

Solution

The given points are $P(1,2,3)$ and $Q(4,5,6)$.

$ \begin{aligned} & \therefore \overrightarrow{{}PQ}=(4-1) \hat{i}+(5-2) \hat{j}+(6-3) \hat{k}=3 \hat{i}+3 \hat{j}+3 \hat{k} \\ & |\overrightarrow{{}PQ}|=\sqrt{3^{2}+3^{2}+3^{2}}=\sqrt{9+9+9}=\sqrt{27}=3 \sqrt{3} \end{aligned} $

Hence, the unit vector in the direction of $\overrightarrow{{}PQ}$ is

$ \frac{\overrightarrow{{}PQ}}{|\overrightarrow{{}PQ}|}=\frac{3 \hat{i}+3 \hat{j}+3 \hat{k}}{3 \sqrt{3}}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k} $

9. For given vectors, $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ and $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$, find the unit vector in the direction of the vector $\vec{a}+\vec{b}$.

Show Answer

Solution

The given vectors are $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ and $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$.

$\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$

$\vec{b}=-\hat{i}+\hat{j}-\hat{k}$

$\therefore \vec{a}+\vec{b}=(2-1) \hat{i}+(-1+1) \hat{j}+(2-1) \hat{k}=1 \hat{i}+0 \hat{j}+1 \hat{k}=\hat{i}+\hat{k}$

$|\vec{a}+\vec{b}|=\sqrt{1^{2}+1^{2}}=\sqrt{2}$

Hence, the unit vector in the direction of $(\vec{a}+\vec{b})$ is

$\frac{(\vec{a}+\vec{b})}{|\vec{a}+\vec{b}|}=\frac{\hat{i}+\hat{k}}{\sqrt{2}}=\frac{1}{\sqrt{2}} \hat{i}+\frac{1}{\sqrt{2}} \hat{k}$

10. Find a vector in the direction of vector $5 \hat{i}-\hat{j}+2 \hat{k}$ which has magnitude 8 units.

Show Answer

Solution

Let $\vec{a}=5 \hat{i}-\hat{j}+2 \hat{k}$.

$\therefore|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}$

$\therefore \hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}$

Hence, the vector in the direction of vector $5 \hat{i}-\hat{j}+2 \hat{k}$ which has magnitude 8 units is given by,

$8 \hat{a}=8(\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}})=\frac{40}{\sqrt{30}} \hat{i}-\frac{8}{\sqrt{30}} \hat{j}+\frac{16}{\sqrt{30}} \hat{k}$

$ \begin{aligned} & =8(\frac{5 \vec{i}-\vec{j}+2 \vec{k}}{\sqrt{30}}) \\ & =\frac{40}{\sqrt{30}} \vec{i}-\frac{8}{\sqrt{30}} \vec{j}+\frac{16}{\sqrt{30}} \vec{k} \end{aligned} $

11. Show that the vectors $2 \hat{i}-3 \hat{j}+4 \hat{k}$ and $-4 \hat{i}+6 \hat{j}-8 \hat{k}$ are collinear.

Show Answer

Solution

Let $\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}$ and $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}$.

It is observed that $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}=-2(2 \hat{i}-3 \hat{j}+4 \hat{k})=-2 \vec{a}$

$\therefore \vec{b}=\lambda \vec{a}$

where,

$\lambda=-2$

Hence, the given vectors are collinear.

12. Find the direction cosines of the vector $\hat{i}+2 \hat{j}+3 \hat{k}$.

Show Answer

Solution

Let $\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}$.

$\therefore|\vec{a}|=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$

Hence, the direction cosines of $\vec{a}$ are $(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}})$.

13. Find the direction cosines of the vector joining the points $A(1,2,-3)$ and $B(-1,-2,1)$, directed from $A$ to $B$.

Show Answer

Solution

The given points are $A(1,2,-3)$ and $B(-1,-2,1)$. $\therefore \overrightarrow{{}AB}=(-1-1) \hat{i}+(-2-2) \hat{j}+{1-(-3)} \hat{k}$

$\Rightarrow \overrightarrow{{}AB}=-2 \hat{i}-4 \hat{j}+4 \hat{k}$

$\therefore|\overrightarrow{{}AB}|=\sqrt{(-2)^{2}+(-4)^{2}+4^{2}}=\sqrt{4+16+16}=\sqrt{36}=6$

Hence, the direction cosines of $\overrightarrow{{}AB}$ are $(-\frac{2}{6},-\frac{4}{6}, \frac{4}{6})=(-\frac{1}{3},-\frac{2}{3}, \frac{2}{3})$.

14. Show that the vector $\hat{i}+\hat{j}+\hat{k}$ is equally inclined to the axes OX, OY and OZ.

Show Answer

Solution

Let $\vec{a}=\hat{i}+\hat{j}+\hat{k}$.

Then,

$|\vec{a}|=\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}$

Therefore, the direction cosines of $\vec{a}$ are $(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$.

Now, let $a, \beta$, and $y$ be the angles formed by $\vec{a}$ with the positive directions of $x, y$, and $z$ axes.

Then, we have $\cos \alpha=\frac{1}{\sqrt{3}}, \cos \beta=\frac{1}{\sqrt{3}}, \cos \gamma=\frac{1}{\sqrt{3}}$.

Hence, the given vector is equally inclined to axes OX, OY, and OZ.

15. Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$ whose position vectors are $\hat{i}+2 \hat{j}-\hat{k}$ and $-\hat{i}+\hat{j}+\hat{k}$ respectively, in the ratio $2: 1$

(i) internally

(ii) externally

Show Answer

Solution

The position vector of point $R$ dividing the line segment joining two points $P$ and $Q$ in the ratio $m: n$ is given by:

i. Internally: $\frac{m \vec{b}+n \vec{a}}{m+n}$

ii. Externally:

$\frac{m \vec{b}-n \vec{a}}{m-n}$

Position vectors of $P$ and $Q$ are given as:

$\overrightarrow{{}OP}=\hat{i}+2 \hat{j}-\hat{k}$ and $\overrightarrow{{}OQ}=-\hat{i}+\hat{j}+\hat{k}$

(i) The position vector of point $R$ which divides the line joining two points $P$ and $Q$ internally in the ratio $2: 1$ is given by,

$ \begin{aligned} \overrightarrow{{}OR} & =\frac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2 \hat{j}-\hat{k})}{2+1}=\frac{(-2 \hat{i}+2 \hat{j}+2 \hat{k})+(\hat{i}+2 \hat{j}-\hat{k})}{3} \\ & =\frac{-\hat{i}+4 \hat{j}+\hat{k}}{3}=-\frac{1}{3} \hat{i}+\frac{4}{3} \hat{j}+\frac{1}{3} \hat{k} \end{aligned} $

(ii) The position vector of point $R$ which divides the line joining two points $P$ and $Q$ externally in the ratio $2: 1$ is given by,

$ \begin{aligned} \overrightarrow{{}OR} & =\frac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2 \hat{j}-\hat{k})}{2-1}=(-2 \hat{i}+2 \hat{j}+2 \hat{k})-(\hat{i}+2 \hat{j}-\hat{k}) \\ & =-3 \hat{i}+3 \hat{k} \end{aligned} $

16. Find the position vector of the mid point of the vector joining the points $P(2,3,4)$ and $Q(4,1,-2)$.

Show Answer

Solution

The position vector of mid-point $R$ of the vector joining points $P(2,3,4)$ and $Q(4,1$, 2) is given by,

$ \begin{aligned} \overrightarrow{{}OR} & =\frac{(2 \hat{i}+3 \hat{j}+4 \hat{k})+(4 \hat{i}+\hat{j}-2 \hat{k})}{2}=\frac{(2+4) \hat{i}+(3+1) \hat{j}+(4-2) \hat{k}}{2} \\ & =\frac{6 \hat{i}+4 \hat{j}+2 \hat{k}}{2}=3 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $

17. Show that the points $A, B$ and $C$ with position vectors, $\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}$, $\vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$, respectively form the vertices of a right angled triangle.

Show Answer

Solution

Position vectors of points $A, B$, and $C$ are respectively given as:

$\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$

$\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$

$\therefore \overrightarrow{{}AB}=\vec{b}-\vec{a}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k}$

$\overrightarrow{{}BC}=\vec{c}-\vec{b}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k}$

$\overrightarrow{{}CA}=\vec{a}-\vec{c}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k}$

$\therefore|\overrightarrow{{}AB}|^{2}=(-1)^{2}+3^{2}+5^{2}=1+9+25=35$

$|\overrightarrow{{}BC}|^{2}=(-1)^{2}+(-2)^{2}+(-6)^{2}=1+4+36=41$

$|\overrightarrow{{}CA}|^{2}=2^{2}+(-1)^{2}+1^{2}=4+1+1=6$

$\therefore|\overrightarrow{{}AB}|^{2}+|\overrightarrow{{}CA}|^{2}=36+6=41=|\overrightarrow{{}BC}|^{2}$

Hence, $A B C$ is a right-angled triangle.

18. In triangle $ABC$ (Fig 10.18), which of the following is not true:

$\quad\quad$(A) $\overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\quad\quad$(B) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\quad\quad$(C) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\quad\quad$(D) $\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

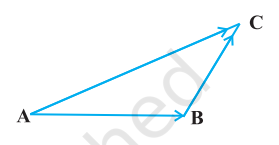
Fig 10.18

Show Answer

Solution

On applying the triangle law of addition in the given triangle, we have:

$$ \begin{align*} & \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC} \tag{1}\\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=-\overrightarrow{{}CA} \\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0} \tag{2} \end{align*} $$

$\therefore$ The equation given in alternative $A$ is true.

$\overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC}$

$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\therefore$ The equation given in alternative $B$ is true.

From equation (2), we have:

$\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\therefore$ The equation given in alternative $D$ is true.

Now, consider the equation given in alternative $C$ :

$\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}CA}$

From equations (1) and (3), we have:

$ \overrightarrow{{}AC}=\overrightarrow{{}CA} $

$\Rightarrow \overrightarrow{{}AC}=-\overrightarrow{{}AC}$

$\Rightarrow \overrightarrow{{}AC}+\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\Rightarrow 2 \overrightarrow{{}AC}=\overrightarrow{{}0}$

$\Rightarrow \overrightarrow{{}AC}=\overrightarrow{{}0}$, which is not true.

Hence, the equation given in alternative $C$ is incorrect.

The correct answer is $\mathbf{C}$.

19. If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then which of the following are incorrect:

(A) $\vec{b}=\lambda \vec{a}$, for some scalar $\lambda$

(B) $\vec{a}= \pm \vec{b}$

(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional

(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.

Show Answer

Solution

If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then they are parallel.

Therefore, we have:

$\vec{b}=\lambda \vec{a}$ (For some scalar $\lambda$ )

If $\lambda= \pm 1$, then $\vec{a}= \pm \vec{b}$.

If $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, then

$\vec{b}=\lambda \vec{a}$.

$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k})$

$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=(\lambda a_1) \hat{i}+(\lambda a_2) \hat{j}+(\lambda a_3) \hat{k}$

$\Rightarrow b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3$

$\Rightarrow \frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}=\lambda$

Thus, the respective components of $\vec{a}$ and $\vec{b}$ are proportional.

However, vectors $\vec{a}$ and $\vec{b}$ can have different directions.

Hence, the statement given in $\mathbf{D}$ is incorrect.

The correct answer is $\mathbf{D}$.

10.6 Product of Two Vectors

So far we have studied about addition and subtraction of vectors. An other algebraic operation which we intend to discuss regarding vectors is their product. We may recall that product of two numbers is a number, product of two matrices is again a matrix. But in case of functions, we may multiply them in two ways, namely, multiplication of two functions pointwise and composition of two functions. Similarly, multiplication of two vectors is also defined in two ways, namely, scalar (or dot) product where the result is a scalar, and vector (or cross) product where the result is a vector. Based upon these two types of products for vectors, they have found various applications in geometry, mechanics and engineering. In this section, we will discuss these two types of products.

10.6.1 Scalar (or dot) product of two vectors

Definition 2 The scalar product of two nonzero vectors $\vec{a}$ and $\vec{b}$, denoted by $\vec{a} \cdot \vec{b}$, is defined as $ \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta $ where, $\theta$ is the angle between $\vec{a}$ and $\vec{b}, 0 \leq \theta \leq \pi$ (Fig 10.19). If either $\vec{a}=0$ or $\vec{b}=0$ then $\theta$ is not defined, and in this case, we define $\vec{a} \cdot \vec{b}=0$

Fig 10.19

Observations

1. $\vec{a} \cdot \vec{b}$ is a real number.

2. Let $\vec{a}$ and $\vec{b}$ be two nonzero vectors, then $\vec{a} \cdot \vec{b}=0$ if and only if $\vec{a}$ and $\vec{b}$ are perpendicular to each other. i.e.$$\vec{a} \cdot \vec{b}=0 \leftrightarrow \vec{a} \perp \vec{b}$$

3. If $\theta=0$, then $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$

In particular, $\vec{a} \cdot \vec{a}=|\vec{a}|^{2}$, as $\theta$ in this case is 0 .

4. If $\theta=\pi$, then $\vec{a} \cdot \vec{b}=-|\vec{a}||\vec{b}|$

In particular, $\vec{a} \cdot \vec{b}=-|\vec{a}||\vec{b}|$, as $\theta$ in this case is $\pi$.

5. In view of the Observations 2 and 3 , for mutually perpendicular unit vectors $\hat{i}, \hat{j}$ and $\hat{k}$,

we have $$ \begin{aligned} & \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1, \\ & \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 \end{aligned} $$

6. The angle between two nonzero vectors $\vec{a}$ and $\vec{b}$ is given by

$$ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}, \text{ or } \theta=\cos ^{-1}(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}) $$

7. The scalar product is commutative. i.e.

$$ \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} $$

Two important properties of scalar product

Property 1 (Distributivity of scalar product over addition) Let $\vec{a}, \vec{b}$ and $\vec{c}$ be any three vectors, then

$ \vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} $

Property 2 Let $\vec{a}$ and $\vec{b}$ be any two vectors, and 1 be any scalar. Then

$$ (\lambda \vec{a}) \cdot \vec{b}=(\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b}) $$

If two vectors $\vec{a}$ and $\vec{b}$ are given in component form as $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, then their scalar product is given as

$ \begin{aligned} \vec{a} \cdot \vec{b}= & (a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}) \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 \hat{i} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_2 \hat{j} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_3 \hat{k} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ \text{ Thus } = & a_1 b_1(\hat{i} \cdot \hat{i})+a_1 b_2(\hat{i} \cdot \hat{j})+a_1 b_3(\hat{i} \cdot \hat{k})+a_2 b_1(\hat{j} \cdot \hat{i})+a_2 b_2(\hat{j} \cdot \hat{j})+a_2 b_3(\hat{j} \cdot \hat{k}) +a_3 b_1(\hat{k} \cdot \hat{i})+a_3 b_2(\hat{k} \cdot \hat{j})+a_3 b_3(\hat{k} \cdot \hat{k}) \text{ (Using the above Properties) } 1 \text{ and 2) } \\ = & a_1 b_1+a_2 b_2+a_3 b_3 \qquad \text{ ((Using Observation 5)) } \\ \qquad & \vec{a} \cdot \vec{b}=a_1 b_1+a_2 b_2+a_3 b_3 \end{aligned} $

10.6.2 Projection of a vector on a line

Suppose a vector $\overrightarrow{{}AB}$ makes an angle $\theta$ with a given directed line $l$ (say), in the anticlockwise direction (Fig 10.20). Then the projection of $\overrightarrow{{}AB}$ on $l$ is a vector $\vec{p}$ (say) with magnitude $|\overrightarrow{{}AB}||\cos \theta|$, and the direction of $\vec{p}$ being the same (or opposite) to that of the line $l$, depending upon whether $\cos \theta$ is positive or negative. The vector $\vec{p}$

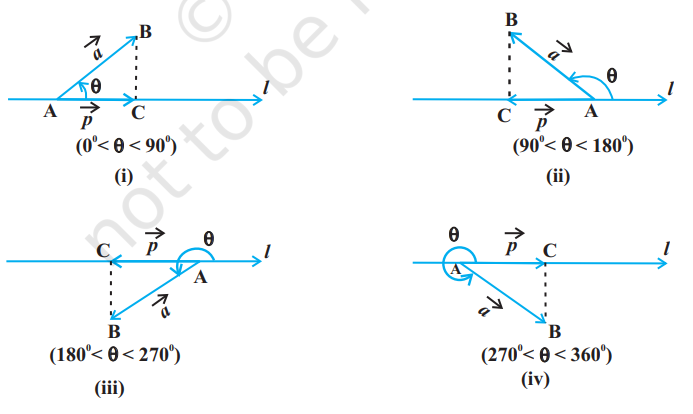
Fig 10.20 is called the projection vector, and its magnitude $|\vec{p}|$ is simply called as the projection of the vector $\overrightarrow{{}AB}$ on the directed line $l$. For example, in each of the following figures (Fig 10.20 (i) to (iv)), projection vector of $\overrightarrow{{}AB}$ along the line $l$ is vector $\overrightarrow{{}AC}$.

Observations

1. If $\hat{p}$ is the unit vector along a line $l$, then the projection of a vector $\vec{a}$ on the line $l$ is given by $\vec{a} \cdot \hat{p}$.

2. Projection of a vector $\vec{a}$ on other vector $\vec{b}$, is given by $$ \vec{a} \cdot \hat{b}, \quad \text{ or } \quad \vec{a} \cdot(\frac{\vec{b}}{|\vec{b}|}), \text{ or } \frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b}) $$

3. If $\theta=0$, then the projection vector of $\overrightarrow{{}A B}$ will be $\overrightarrow{{}A B}$ itself and if $\theta=\pi$, then the projection vector of $\overrightarrow{{}AB}$ will be $\overrightarrow{{}BA}$.

4. If $\theta=\frac{\pi}{2}$ or $\theta=\frac{3 \pi}{2}$, then the projection vector of $\overrightarrow{{}A B}$ will be zero vector.

Remark If $\alpha, \beta$ and $\gamma$ are the direction angles of vector $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$, then its direction cosines may be given as

$$ \cos \alpha=\frac{\vec{a} \cdot \hat{i}}{|\vec{a}||\hat{i}|}=\frac{a_1}{|\vec{a}|}, \cos \beta=\frac{a_2}{|\vec{a}|}, \text{ and } \cos \gamma=\frac{a_3}{|\vec{a}|} $$

Also, note that $|\vec{a}| \cos \alpha,|\vec{a}| \cos \beta$ and $|\vec{a}| \cos \gamma$ are respectively the projections of $\vec{a}$ along $OX, OY$ and $OZ$. i.e., the scalar components $a_1, a_2$ and $a_3$ of the vector $\vec{a}$, are precisely the projections of $\vec{a}$ along $x$-axis, $y$-axis and $z$-axis, respectively. Further, if $\vec{a}$ is a unit vector, then it may be expressed in terms of its direction cosines as

$$ \vec{a}=\cos \alpha \hat{i}+\cos \beta \hat{j}+\cos \gamma \hat{k} $$

Example 13 Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes 1 and 2 respectively and when $\vec{a} \cdot \vec{b}=1$.

Solution Given $\vec{a} \cdot \vec{b}=1,|\vec{a}|=1$ and $|\vec{b}|=2$. We have

$$ \theta=\cos ^{-1}(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|})=\cos ^{-1}(\frac{1}{2})=\frac{\pi}{3} $$

Example 14 Find angle ’ $\theta$ ’ between the vectors $\vec{a}=\hat{i}+\hat{j}-\hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+\hat{k}$.

Solution The angle $\theta$ between two vectors $\vec{a}$ and $\vec{b}$ is given by

Now $$ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} $$

Therefore, we have $\quad \cos \theta=\frac{-1}{3}$

hence the required angle is $$ \theta=\cos ^{-1}(-\frac{1}{3}) $$

Example 15 If $\vec{a}=5 \hat{i}-\hat{j}-3 \hat{k}$ and $\vec{b}=\hat{i}+3 \hat{j}-5 \hat{k}$, then show that the vectors $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ are perpendicular.

Solution We know that two nonzero vectors are perpendicular if their scalar product is zero.

Here $$ \vec{a}+\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})+(\hat{i}+3 \hat{j}-5 \hat{k})=6 \hat{i}+2 \hat{j}-8 \hat{k} $$

and $$ \vec{a}-\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})-(\hat{i}+3 \hat{j}-5 \hat{k})=4 \hat{i}-4 \hat{j}+2 \hat{k} $$

So $$ (\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=(6 \hat{i}+2 \hat{j}-8 \hat{k}) \cdot(4 \hat{i}-4 \hat{j}+2 \hat{k})=24-8-16=0 $$

Hence $\quad \vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ are perpendicular vectors.

Example 16 Find the projection of the vector $\vec{a}=2 \hat{i}+3 \hat{j}+2 \hat{k}$ on the vector $\vec{b}=\hat{i}+2 \hat{j}+\hat{k}$

Solution The projection of vector $\vec{a}$ on the vector $\vec{b}$ is given by

$$ \frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{(2 \times 1+3 \times 2+2 \times 1)}{\sqrt{(1)^{2}+(2)^{2}+(1)^{2}}}=\frac{10}{\sqrt{6}}=\frac{5}{3} \sqrt{6} $$

Example 17 Find $|\vec{a}-\vec{b}|$, if two vectors $\vec{a}$ and $\vec{b}$ are such that $|\vec{a}|=2,|\vec{b}|=3$ and $\vec{a} \cdot \vec{b}=4$.

Solution We have

$$ \begin{aligned} |\vec{a}-\vec{b}|^{2} & =(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{b}) \\ & =\vec{a} \cdot \vec{a}-\vec{a} \cdot \vec{b}-\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \end{aligned} $$ $$ \begin{aligned} & =|\vec{a}|^{2}-2(\vec{a} \cdot \vec{b})+|\vec{b}|^{2} \\ & =(2)^{2}-2(4)+(3)^{2} \end{aligned} $$

Example 18 If $\vec{a}$ is a unit vector and $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8$, then find $|\vec{x}|$.

Solution Since $\vec{a}$ is a unit vector, $|\vec{a}|=1$. Also,

$$ (\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8 $$

or $ \vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\vec{a} \cdot \vec{a}=8 $

or $ |\vec{x}|^{2}-1=8 \text{ i.e. }|\vec{x}|^{2}=9 $

Therefore $|\vec{x}|=3 $ (as magnitude of a vector is non negative).

Example 19 For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$ (CauchySchwartz inequality).

Solution The inequality holds trivially when either $\vec{a}=\overrightarrow{{}0}$ or $\vec{b}=\overrightarrow{{}0}$. Actually, in such a situation we have $|\vec{a} \cdot \vec{b}|=0=|\vec{a}||\vec{b}|$. So, let us assume that $|\vec{a}| \neq 0 \neq|\vec{b}|$.

Then, we have Therefore $$ \frac{|\vec{a} \cdot \vec{b}|}{|\vec{a} | \vec{b}|}=|\cos \theta| \leq 1 $$

$\quad|\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$

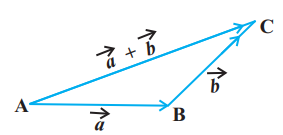
Fig 10.21

Example 20 For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$ (triangle inequality).

Solution The inequality holds trivially in case either

$$ \begin{aligned} |\vec{a}+\vec{b}|^{2}= & (\vec{a}+\vec{b})^{2}=(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b}) \\ = & \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \\ = & |\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a} \cdot \vec{b}|+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a}||\vec{b}|+|\vec{b}|^{2} \\ = & (|\vec{a}|+|\vec{b}|)^{2} \\ & |\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}| \end{aligned} $$

Remark If the equality holds in triangle inequality (in the above Example 20 ), i.e.

then $$ \begin{aligned} |\vec{a}+\vec{b}| & =|\vec{a}|+|\vec{b}| \\ |\overrightarrow{{}AC}| & =|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}| \end{aligned} $$

showing that the points $A, B$ and $C$ are collinear.

Example 21 Show that the points $A(-2 \hat{i}+3 \hat{j}+5 \hat{k}), B(\hat{i}+2 \hat{j}+3 \hat{k})$ and $C(7 \hat{i}-\hat{k})$ are collinear.

Solution We have

$$ \begin{aligned} \overrightarrow{{}AB} & =(1+2) \hat{i}+(2-3) \hat{j}+(3-5) \hat{k}=3 \hat{i}-\hat{j}-2 \hat{k} \\ \overrightarrow{{}BC} & =(7-1) \hat{i}+(0-2) \hat{j}+(-1-3) \hat{k}=6 \hat{i}-2 \hat{j}-4 \hat{k} \\ \overrightarrow{{}AC} & =(7+2) \hat{i}+(0-3) \hat{j}+(-1-5) \hat{k}=9 \hat{i}-3 \hat{j}-6 \hat{k} \\ |\overrightarrow{{}AB}| & =\sqrt{14},|\overrightarrow{{}BC}|=2 \sqrt{14} \text{ and }|\overrightarrow{{}AC}|=3 \sqrt{14} \end{aligned} $$

Therefore $$ |\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}| $$

Hence the points A, B and C are collinear.

Note In Example 21 , one may note that although $\overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0}$ but the points $A, B$ and $C$ do not form the vertices of a triangle.

EXERCISE 10.3

1. Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes $\sqrt{3}$ and 2 , respectively having $\vec{a} \cdot \vec{b}=\sqrt{6}$.

Show Answer

Solution

It is given that,

$|\vec{a}|=\sqrt{3},|\vec{b}|=2$ and, $\vec{a} \cdot \vec{b}=\sqrt{6}$

Now, we know that $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$.

$\therefore \sqrt{6}=\sqrt{3} \times 2 \times \cos \theta$

$\Rightarrow \cos \theta=\frac{\sqrt{6}}{\sqrt{3} \times 2}$

$\Rightarrow \cos \theta=\frac{1}{\sqrt{2}}$

$\Rightarrow \theta=\frac{\pi}{4}$

Hence, the angle between the given vectors $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$.

2. Find the angle between the vectors $\hat{i}-2 \hat{j}+3 \hat{k}$ and $3 \hat{i}-2 \hat{j}+\hat{k}$

Show Answer

Solution

The given vectors are $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ and $\vec{b}=3 \hat{i}-2 \hat{j}+\hat{k}$.

$ \begin{aligned} & |\vec{a}|=\sqrt{1^{2}+(-2)^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14} \\ & |\vec{b}|=\sqrt{3^{2}+(-2)^{2}+1^{2}}=\sqrt{9+4+1}=\sqrt{14} \end{aligned} $

Now, $\vec{a} \cdot \vec{b}=(\hat{i}-2 \hat{j}+3 \hat{k})(3 \hat{i}-2 \hat{j}+\hat{k})$

$ \begin{aligned} & =1.3+(-2)(-2)+3.1 \\ & =3+4+3 \\ & =10 \end{aligned} $

Also, we know that $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$

$\therefore 10=\sqrt{14} \sqrt{14} \cos \theta$

$\Rightarrow \cos \theta=\frac{10}{14}$

$\Rightarrow \theta=\cos ^{-1}(\frac{5}{7})$

3. Find the projection of the vector $\hat{i}-\hat{j}$ on the vector $\hat{i}+\hat{j}$.

Show Answer

Solution

Let $\vec{a}=\hat{i}-\hat{j}$ and $\vec{b}=\hat{i}+\hat{j}$.

Now, projection of vector $\vec{a}$ on $\vec{b}$ is given by,

$\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{1}{\sqrt{1+1}}{1.1+(-1)(1)}=\frac{1}{\sqrt{2}}(1-1)=0$

Hence, the projection of vector $\vec{a}$ on $\vec{b}$ is 0 .

4. Find the projection of the vector $\hat{i}+3 \hat{j}+7 \hat{k}$ on the vector $7 \hat{i}-\hat{j}+8 \hat{k}$.

Show Answer

Solution

Let $\vec{a}=\hat{i}+3 \hat{j}+7 \hat{k}$ and $\hat{b}=7 \hat{i}-\hat{j}+8 \hat{k}$.

Now, projection of vector $\vec{a}$ on $\vec{b}$ is given by, $\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{1}{\sqrt{7^{2}+(-1)^{2}+8^{2}}}{1(7)+3(-1)+7(8)}=\frac{7-3+56}{\sqrt{49+1+64}}=\frac{60}{\sqrt{114}}$

5. Show that each of the given three vectors is a unit vector:

$$ \frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k}), \frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k}), \quad \frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k}) $$

Also, show that they are mutually perpendicular to each other.

Show Answer

Solution

Let $\vec{a}=\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k})=\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}$,

$\vec{b}=\frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k})=\frac{3}{7} \hat{i}-\frac{6}{7} \hat{j}+\frac{2}{7} \hat{k}$,

$\vec{c}=\frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})=\frac{6}{7} \hat{i}+\frac{2}{7} \hat{j}-\frac{3}{7} \hat{k}$.

$|\vec{a}|=\sqrt{(\frac{2}{7})^{2}+(\frac{3}{7})^{2}+(\frac{6}{7})^{2}}=\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}=1$

$|\vec{b}|=\sqrt{(\frac{3}{7})^{2}+(-\frac{6}{7})^{2}+(\frac{2}{7})^{2}}=\sqrt{\frac{9}{49}+\frac{36}{49}+\frac{4}{49}}=1$

$|\vec{c}|=\sqrt{(\frac{6}{7})^{2}+(\frac{2}{7})^{2}+(-\frac{3}{7})^{2}}=\sqrt{\frac{36}{49}+\frac{4}{49}+\frac{9}{49}}=1$

Thus, each of the given three vectors is a unit vector.

$\vec{a} \cdot \vec{b}=\frac{2}{7} \times \frac{3}{7}+\frac{3}{7} \times(\frac{-6}{7})+\frac{6}{7} \times \frac{2}{7}=\frac{6}{49}-\frac{18}{49}+\frac{12}{49}=0$

$\vec{b} \cdot \vec{c}=\frac{3}{7} \times \frac{6}{7}+(\frac{-6}{7}) \times \frac{2}{7}+\frac{2}{7} \times(\frac{-3}{7})=\frac{18}{49}-\frac{12}{49}-\frac{6}{49}=0$

$\vec{c} \cdot \vec{a}=\frac{6}{7} \times \frac{2}{7}+\frac{2}{7} \times \frac{3}{7}+(\frac{-3}{7}) \times \frac{6}{7}=\frac{12}{49}+\frac{6}{49}-\frac{18}{49}=0$

Hence, the given three vectors are mutually perpendicular to each other.

6. Find $|\vec{a}|$ and $|\vec{b}|$, if $(\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=8$ and $|\vec{a}|=8|\vec{b}|$.

Show Answer

Solution

$(\vec{a} \cdot \vec{b}) \cdot(\vec{a}-\vec{b})=8$

$\Rightarrow \vec{a} \cdot \vec{a}-\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}-\vec{b} \cdot \vec{b}=8$

$\Rightarrow|\vec{a}|^{2}-|\vec{b}|^{2}=8$

$\Rightarrow(8|\vec{b}|)^{2}-|\vec{b}|^{2}=8 \quad[|\vec{a}|=8|\vec{b}|]$

$\Rightarrow 64|\vec{b}|^{2}-|\vec{b}|^{2}=8$

$\Rightarrow 63|\vec{b}|^{2}=8$

$\Rightarrow|\vec{b}|^{2}=\frac{8}{63}$

$\Rightarrow|\vec{b}|=\sqrt{\frac{8}{63}} \quad$ [Magnitude of a vector is non-negative]

$\Rightarrow|\vec{b}|=\frac{2 \sqrt{2}}{3 \sqrt{7}}$

$|\vec{a}|=8|\vec{b}|=\frac{8 \times 2 \sqrt{2}}{3 \sqrt{7}}=\frac{16 \sqrt{2}}{3 \sqrt{7}}$

7. Evaluate the product $(3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})$.

Show Answer

Solution

$ \begin{aligned} & (3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b}) \\ & =3 \vec{a} \cdot 2 \vec{a}+3 \vec{a} \cdot 7 \vec{b}-5 \vec{b} \cdot 2 \vec{a}-5 \vec{b} \cdot 7 \vec{b} \\ & =6 \vec{a} \cdot \vec{a}+21 \vec{a} \cdot \vec{b}-10 \vec{a} \cdot \vec{b}-35 \vec{b} \cdot \vec{b} \\ & =6|\vec{a}|^{2}+11 \vec{a} \cdot \vec{b}-35|\vec{b}|^{2} \end{aligned} $

8. Find the magnitude of two vectors $\vec{a}$ and $\vec{b}$, having the same magnitude and such that the angle between them is $60^{\circ}$ and their scalar product is $\frac{1}{2}$.

Show Answer

Solution

Let $\theta$ be the angle between the vectors $\vec{a}$ and $\vec{b}$.

It is given that $|\vec{a}|=|\vec{b}|, \vec{a} \cdot \vec{b}=\frac{1}{2}$, and $\theta=60^{\circ}$.

We know that $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$

$\therefore \frac{1}{2}=|\vec{a}||\vec{a}| \cos 60^{\circ}$

[Using (1)]

$\Rightarrow \frac{1}{2}=|\vec{a}|^{2} \times \frac{1}{2}$

$\Rightarrow|\vec{a}|^{2}=1$

$\Rightarrow|\vec{a}|=|\vec{b}|=1$

9. Find $|\vec{x}|$, if for a unit vector $\vec{a},(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12$.

Show Answer

Solution

$(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12$

$\Rightarrow \vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\bar{{}a} \cdot \vec{a}=12$

$\Rightarrow|\vec{x}|^{2}-|\vec{a}|^{2}=12$

$\Rightarrow|\vec{x}|^{2}-1=12 \quad[|\vec{a}|=1$ as $\vec{a}$ is a unit vector $]$

$\Rightarrow|\vec{x}|^{2}=13$

$\therefore|\vec{x}|=\sqrt{13}$

10. If $\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$ and $\vec{c}=3 \hat{i}+\hat{j}$ are such that $\vec{a}+\lambda \vec{b}$ is perpendicular to $\vec{c}$, then find the value of $\lambda$.

Show Answer

Solution

The given vectors are $\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$, and $\vec{c}=3 \hat{i}+\hat{j}$.

Now,

$\vec{a}+\lambda \vec{b}=(2 \hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{i}+2 \hat{j}+\hat{k})=(2-\lambda) \hat{i}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}$

If $(\vec{a}+\lambda \vec{b})$ is perpendicular to $\vec{c}$, then

$(\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0$.

$\Rightarrow[(2-\lambda) \hat{i}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}] \cdot(3 \hat{i}+\hat{j})=0$

$\Rightarrow(2-\lambda) 3+(2+2 \lambda) 1+(3+\lambda) 0=0$

$\Rightarrow 6-3 \lambda+2+2 \lambda=0$

$\Rightarrow-\lambda+8=0$

$\Rightarrow \lambda=8$

Hence, the required value of $\lambda$ is 8 .

11. Show that $|\vec{a}| \vec{b}+|\vec{b}| \vec{a}$ is perpendicular to $|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$, for any two nonzero vectors $\vec{a}$ and $\vec{b}$.

Show Answer

Solution

$(|\vec{a}| \vec{b}+|\vec{b}| \vec{a}) \cdot(|\vec{a}| \vec{b}-|\vec{b}| \vec{a})$

$=|\vec{a}|^{2} \vec{b} \cdot \vec{b}-|\vec{a}||\vec{b}| \vec{b} \cdot \vec{a}+|\vec{b}||\vec{a}| \vec{a} \cdot \vec{b}-|\vec{b}|^{2} \vec{a} \cdot \vec{a}$

$=|\vec{a}|^{2}|\vec{b}|^{2}-|\vec{b}|^{2}|\vec{a}|^{2}$

$=0$

Hence, $|\vec{a}| \vec{b}+|\vec{b}| \vec{a}$ and $|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ are perpendicular to each other.

12. If $\vec{a} \cdot \vec{a}=0$ and $\vec{a} \cdot \vec{b}=0$, then what can be concluded about the vector $\vec{b}$ ?

Show Answer

Solution

It is given that $\vec{a} \cdot \vec{a}=0$ and $\vec{a} \cdot \vec{b}=0$.

Now,

$\vec{a} \cdot \vec{a}=0 \Rightarrow|\vec{a}|^{2}=0 \Rightarrow|\vec{a}|=0$

$\therefore \vec{a}$ is a zero vector.

Hence, vector $\vec{b}$ satisfying $\vec{a} \cdot \vec{b}=0$ can be any vector.

13. If $\vec{a}, \vec{b}, \vec{c}$ are unit vectors such that $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$, find the value of $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$.

Show Answer

Solution

We have $|\overrightarrow{\mathrm{a}}|=1,|\overrightarrow{\mathrm{b}}|=1,|\overrightarrow{\mathrm{c}}|=1$

Also $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$

Squaring we get, $$ \begin{aligned} & |\overrightarrow{\mathrm{a}}|^2+|\overrightarrow{\mathrm{b}}|^2+|\overrightarrow{\mathrm{c}}|^2+2(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}})=0 \\ & \Rightarrow 1+1+1+2(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}})=0 \\ & \therefore \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}}=-\frac{3}{2} \end{aligned} $$

14. If either vector $\vec{a}=\overrightarrow{{}0}$ or $\vec{b}=\overrightarrow{{}0}$, then $\vec{a} \cdot \vec{b}=0$. But the converse need not be true. Justify your answer with an example.

Show Answer

Solution

Consider $\vec{a}=2 \hat{i}+4 \hat{j}+3 \hat{k}$ and $\vec{b}=3 \hat{i}+3 \hat{j}-6 \hat{k}$.

Then,

$\vec{a} \cdot \vec{b}=2.3+4.3+3(-6)=6+12-18=0$

We now observe that:

$|\vec{a}|=\sqrt{2^{2}+4^{2}+3^{2}}=\sqrt{29}$

$\therefore \vec{a} \neq \overrightarrow{{}0}$

$|\vec{b}|=\sqrt{3^{2}+3^{2}+(-6)^{2}}=\sqrt{54}$

$\therefore \vec{b} \neq \overrightarrow{{}0}$

Hence, the converse of the given statement need not be true.

15. If the vertices $A, B, C$ of a triangle $ABC$ are $(1,2,3),(-1,0,0),(0,1,2)$, respectively, then find $\angle ABC$. [ $\angle ABC$ is the angle between the vectors $\overrightarrow{{}BA}$ and $\overrightarrow{{}BC}$].

Show Answer

Solution

The vertices of $\triangle A B C$ are given as $A(1,2,3), B(-1,0,0)$, and $C(0,1,2)$.

Also, it is given that $\square ABC$ is the angle between the vectors $\overrightarrow{{}BA}$ and $\overrightarrow{{}BC}$.

$ \begin{aligned} & \overrightarrow{{}BA}={1-(-1)} \hat{i}+(2-0) \hat{j}+(3-0) \hat{k}=2 \hat{i}+2 \hat{j}+3 \hat{k} \\ & \overrightarrow{{}BC}={0-(-1)} \hat{i}+(1-0) \hat{j}+(2-0) \hat{k}=\hat{i}+\hat{j}+2 \hat{k} \\ & \therefore \overrightarrow{{}BA} \cdot \overrightarrow{{}BC}=(2 \hat{i}+2 \hat{j}+3 \hat{k}) \cdot(\hat{i}+\hat{j}+2 \hat{k})=2 \times 1+2 \times 1+3 \times 2=2+2+6=10 \\ & \mid \overrightarrow{{}BA}=\sqrt{2^{2}+2^{2}+3^{2}}=\sqrt{4+4+9}=\sqrt{17} \\ & \mid \overrightarrow{{}BC}=\sqrt{1+1+2^{2}}=\sqrt{6} \end{aligned} $

Now, it is known that:

$\overrightarrow{{}BA} \cdot \overrightarrow{{}BC}=|\overrightarrow{{}BA}||\overrightarrow{{}BC}| \cos (\angle ABC)$

$\therefore 10=\sqrt{17} \times \sqrt{6} \cos (\angle ABC)$

$\Rightarrow \cos (\angle ABC)=\frac{10}{\sqrt{17} \times \sqrt{6}}$

$\Rightarrow \angle ABC=\cos ^{-1}(\frac{10}{\sqrt{102}})$

16. Show that the points $A(1,2,7), B(2,6,3)$ and $C(3,10,-1)$ are collinear.

Show Answer

Solution

The given points are $A(1,2,7), B(2,6,3)$, and $C(3,10,-1)$.

$\therefore \overrightarrow{{}AB}=(2-1) \hat{i}+(6-2) \hat{j}+(3-7) \hat{k}=\hat{i}+4 \hat{j}-4 \hat{k}$

$ \overrightarrow{{}BC}=(3-2) \hat{i}+(10-6) \hat{j}+(-1-3) \hat{k}=\hat{i}+4 \hat{j}-4 \hat{k} $

$\overrightarrow{{}AC}=(3-1) \hat{i}+(10-2) \hat{j}+(-1-7) \hat{k}=2 \hat{i}+8 \hat{j}-8 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{1^{2}+4^{2}+(-4)^{2}}=\sqrt{1+16+16}=\sqrt{33}$

$|\overrightarrow{{}BC}|=\sqrt{1^{2}+4^{2}+(-4)^{2}}=\sqrt{1+16+16}=\sqrt{33}$

$|\overrightarrow{{}AC}|=\sqrt{2^{2}+8^{2}+8^{2}}=\sqrt{4+64+64}=\sqrt{132}=2 \sqrt{33}$

$\therefore|\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}|$

Hence, the given points A, B, and C are collinear.

17. Show that the vectors $2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}$ and $3 \hat{i}-4 \hat{j}-4 \hat{k}$ form the vertices of a right angled triangle.

Show Answer

Solution

Let vectors $2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}$ and $3 \hat{i}-4 \hat{j}-4 \hat{k}$ be position vectors of points $A, B$, and $C$ respectively.

i.e., $\overrightarrow{{}OA}=2 \hat{i}-\hat{j}+\hat{k}, \overrightarrow{{}OB}=\hat{i}-3 \hat{j}-5 \hat{k}$ and $\overrightarrow{{}OC}=3 \hat{i}-4 \hat{j}-4 \hat{k}$

Now, vectors $\overrightarrow{{}AB}, \overrightarrow{{}BC}$, and $\overrightarrow{{}AC}$ represent the sides of $\triangle ABC$.

i.e., $\overrightarrow{{}OA}=2 \hat{i}-\hat{j}+\hat{k}, \overrightarrow{{}OB}=\hat{i}-3 \hat{j}-5 \hat{k}$, and $\overrightarrow{{}OC}=3 \hat{i}-4 \hat{j}-4 \hat{k}$

$\therefore \overrightarrow{{}AB}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k}$

$\overrightarrow{{}BC}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k}$

$\overrightarrow{{}AC}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{(-1)^{2}+(-2)^{2}+(-6)^{2}}=\sqrt{1+4+36}=\sqrt{41}$

$|\overrightarrow{{}BC}|=\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{4+1+1}=\sqrt{6}$

$|\overrightarrow{{}AC}|=\sqrt{(-1)^{2}+3^{2}+5^{2}}=\sqrt{1+9+25}=\sqrt{35}$

$\therefore|\overrightarrow{{}BC}|^{2}+|\overrightarrow{{}AC}|^{2}=6+35=41=|\overrightarrow{{}AB}|^{2}$

Hence, $\triangle A B C$ is a right-angled triangle.

18. If $\vec{a}$ is a nonzero vector of magnitude ’ $a$ ’ and $\lambda$ a nonzero scalar, then $\lambda \vec{a}$ is unit vector if

(A) $\lambda=1$

(B) $\lambda=-1$

(C) $a=|\lambda|$

(D) $a=1 /|\lambda|$

Show Answer

Solution

Vector $\lambda \vec{a}$ is a unit vector if $|\lambda \vec{a}|=1$.

Now,

$|\lambda \vec{a}|=1$

$\Rightarrow|\lambda||\vec{a}|=1$

$\Rightarrow|\vec{a}|=\frac{1}{|\lambda|}$

$[\lambda \neq 0]$

$\Rightarrow a=\frac{1}{|\lambda|}$

$[|\vec{a}|=a]$

Hence, vector $\lambda \vec{a}$ is a unit vector if $a=\frac{1}{|\lambda|}$. The correct answer is $D$.

10.6.3 Vector (or cross) product of two vectors

In Section 10.2, we have discussed on the three dimensional right handed rectangular coordinate system. In this system, when the positive $x$-axis is rotated counterclockwise into the positive $y$-axis, a right handed (standard) screw would advance in the direction of the positive $z$-axis (Fig 10.22(i)).

In a right handed coordinate system, the thumb of the right hand points in the direction of the positive $z$-axis when the fingers are curled in the direction away from the positive $x$-axis toward the positive $y$-axis (Fig 10.22(ii)).

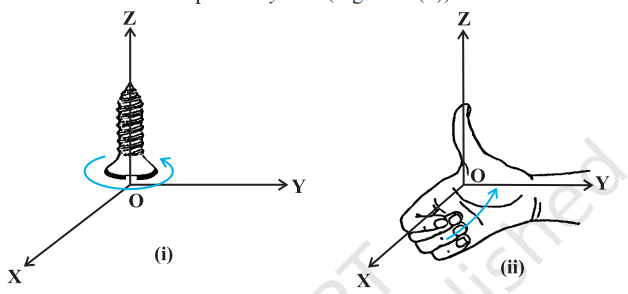
Fig 10.22

Definition 3 The vector product of two nonzero vectors $\vec{a}$ and $\vec{b}$, is denoted by $\vec{a} \times \vec{b}$ and defined as $ \vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n}, $ where, $\theta$ is the angle between $\vec{a}$ and $\vec{b}, 0 \leq \theta \leq \pi$ and $\hat{n}$ is a unit vector perpendicular to both $\vec{a}$ and $\vec{b}$, such that $\vec{a}, \vec{b}$ and $\hat{n}$ form a right handed system (Fig 10.23). i.e., the right handed system rotated from $\vec{a}$ to $\vec{b}$ moves in the direction of $\hat{n}$.

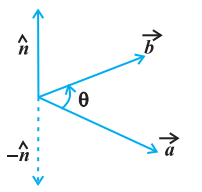
Fig 10.23

If either $\vec{a}=\overrightarrow{{}0}$ or $\vec{b}=\overrightarrow{{}0}$, then $\theta$ is not defined and in this case, we define $\vec{a} \times \vec{b}=\overrightarrow{{}0}$.

Observations

1. $\vec{a} \times \vec{b}$ is a vector.

2. Let $\vec{a}$ and $\vec{b}$ be two nonzero vectors. Then $\vec{a} \times \vec{b}=\overrightarrow{{}0}$ if and only if $\vec{a}$ and $\vec{b}$ are parallel (or collinear) to each other, i.e.,

$ \vec{a} \times \vec{b}=\overrightarrow{{}0} \leftrightarrow \vec{a} || \vec{b} $

In particular, $\vec{a} \times \vec{a}=\overrightarrow{{}0}$ and $\vec{a} \times(-\vec{a})=\overrightarrow{{}0}$, since in the first situation, $\theta=0$ and in the second one, $\theta=\pi$, making the value of $\sin \theta$ to be 0 .

3. If $\theta=\frac{\pi}{2}$ then $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|$.

4. In view of the Observations 2 and 3 , for mutually perpendicular unit vectors $\hat{i}, \hat{j}$ and $\hat{k}$ (Fig 10.24), we have

$ \begin{aligned} & \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{{}0} \\ & \hat{i} \times \hat{j}=\hat{k}, \quad \hat{j} \times \hat{k}=\hat{i}, \quad \hat{k} \times \hat{i}=\hat{j} \end{aligned} $

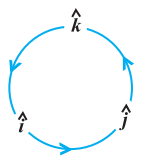
Fig 10.24

5. In terms of vector product, the angle between two vectors $\vec{a}$ and $\vec{b}$ may be given as

$$ \sin \theta=\frac{|\vec{a} \times \vec{b}|}{|\vec{a} | \vec{b}|} $$

6. It is always true that the vector product is not commutative, as $\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}$. Indeed, $\vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n}$, where $\vec{a}, \vec{b}$ and $\hat{n}$ form a right handed system, i.e., $\theta$ is traversed from $\vec{a}$ to $\vec{b}$, Fig 10.25 (i). While, $\vec{b} \times \vec{a}=|\vec{a} | \vec{b}| \sin \theta \hat{n}_1$, where $\vec{b}, \vec{a}$ and $\hat{n}_1$ form a right handed system i.e. $\theta$ is traversed from $\vec{b}$ to $\vec{a}$, Fig 10.25(ii).

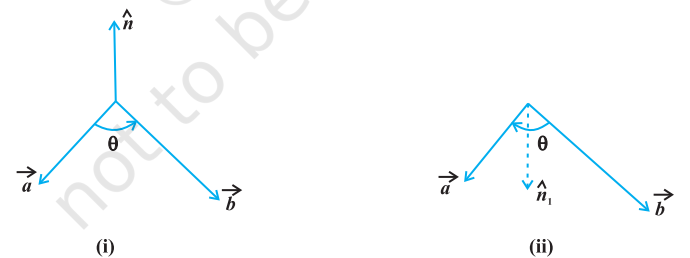
Fig 10.25

Thus, if we assume $\vec{a}$ and $\vec{b}$ to lie in the plane of the paper, then $\hat{n}$ and $\hat{n}_1$ both will be perpendicular to the plane of the paper. But, $\hat{n}$ being directed above the paper while $\hat{n}_1$ directed below the paper. i.e. $\hat{n}_1=-\hat{n}$.

Hence $$ \begin{aligned} \vec{a} \times \vec{b} & =|\vec{a} | \vec{b}| \sin \theta \hat{n} \ & =-|\vec{a} | \vec{b}| \sin \theta \hat{n}_1=-\vec{b} \times \vec{a} \end{aligned} $$

7. In view of the Observations 4 and 6, we have $$ \hat{j} \times \hat{i}=-\hat{k}, \quad \hat{k} \times \hat{j}=-\hat{i} \text { and } \hat{i} \times \hat{k}=-\hat{j} \text {. } $$

8. If $\vec{a}$ and $\vec{b}$ represent the adjacent sides of a triangle then its area is given as $\frac{1}{2}|\vec{a} \times \vec{b}|$. By definition of the area of a triangle, we have from Fig 10.26, Area of triangle $\mathrm{ABC}=\frac{1}{2} \mathrm{AB} \cdot \mathrm{CD}$. But $\mathrm{AB}=|\vec{b}|$ (as given), and $\mathrm{CD}=|\vec{a}| \sin \theta$. Thus, Area of triangle $\mathrm{ABC}=\frac{1}{2}|\vec{b} | \vec{a}| \sin \theta=\frac{1}{2}|\vec{a} \times \vec{b}|$.

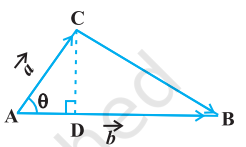
Fig 10.26

9. If $\vec{a}$ and $\vec{b}$ represent the adjacent sides of a triangle then its area is given as $\frac{1}{2}|\vec{a} \times \vec{b}|$. By definition of the area of a triangle, we have from Fig 10.26, Area of triangle $ABC=\frac{1}{2} AB \cdot CD$. But $AB=|\vec{b}|$ (as given), and $CD=|\vec{a}| \sin \theta$. Thus, Area of triangle $ABC=\frac{1}{2}|\vec{b}||\vec{a}| \sin \theta=\frac{1}{2}|\vec{a} \times \vec{b}|$. Area of parallelogram $ABCD=|\vec{b} | \vec{a}| \sin \theta=|\vec{a} \times \vec{b}|$.

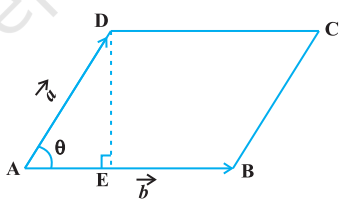
Fig 10.26

We now state two important properties of vector product.

Property 3 (Distributivity of vector product over addition): If $\vec{a}, \vec{b}$ and $\vec{c}$ are any three vectors and $\lambda$ be a scalar, then

(i) $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

(ii) $\lambda(\vec{a} \times \vec{b})=(\lambda \vec{a}) \times \vec{b}=\vec{a} \times(\lambda \vec{b})$

Let $\vec{a}$ and $\vec{b}$ be two vectors given in component form as $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, respectively. Then their cross product may be given by

$$ \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $$

Explanation We have

$$ \begin{aligned} \vec{a} \times \vec{b}= & (a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}) \times(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 b_1(\hat{i} \times \hat{i})+a_1 b_2(\hat{i} \times \hat{j})+a_1 b_3(\hat{i} \times \hat{k})+a_2 b_1(\hat{j} \times \hat{i}) \\ & +a_2 b_2(\hat{j} \times \hat{j})+a_2 b_3(\hat{j} \times \hat{k}) \\ & +a_3 b_1(\hat{k} \times \hat{i})+a_3 b_2(\hat{k} \times \hat{j})+a_3 b_3(\hat{k} \times \hat{k}) \\ = & a_1 b_2(\hat{i} \times \hat{j})-a_1 b_3(\hat{k} \times \hat{i})-a_2 b_1(\hat{i} \times \hat{j}) \\ & +a_2 b_3(\hat{j} \times \hat{k})+a_3 b_1(\hat{k} \times \hat{i})-a_3 b_2(\hat{j} \times \hat{k}) \end{aligned} $$

(by Property 1)

(as $\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0$ and $\hat{i} \times \hat{k}=-\hat{k} \times \hat{i}, \hat{j} \times \hat{i}=-\hat{i} \times \hat{j}$ and $\hat{k} \times \hat{j}=-\hat{j} \times \hat{k}$ )

$$ \begin{aligned} = & a_1 b_2 \hat{k}-a_1 b_3 \hat{j}-a_2 b_1 \hat{k}+a_2 b_3 \hat{i}+a_3 b_1 \hat{j}-a_3 b_2 \hat{i} \\ & (\text{ as } \hat{i} \times \hat{j}=\hat{k}, \hat{j} \times \hat{k}=\hat{i} \text{ and } \hat{k} \times \hat{i}=\hat{j}) \\ = & (a_2 b_3-a_3 b_2) \hat{i}-(a_1 b_3-a_3 b_1) \hat{j}+(a_1 b_2-a_2 b_1) \hat{k} \\ = & \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \end{aligned} $$

Example 22 Find $|\vec{a} \times \vec{b}|$, if $\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}$ and $\vec{b}=3 \hat{i}+5 \hat{j}-2 \hat{k}$

Solution We have

$$ \begin{aligned} \vec{a} \times \vec{b} & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 3 \\ 3 & 5 & -2 \end{vmatrix} \\ & =\hat{i}(-2-15)-(-4-9) \hat{j}+(10-3) \hat{k}=-17 \hat{i}+13 \hat{j}+7 \hat{k} \end{aligned} $$

Hence $|\vec{a} \times \vec{b}|=\sqrt{(-17)^{2}+(13)^{2}+(7)^{2}}=\sqrt{507}$

Example 23 Find a unit vector perpendicular to each of the vectors $(\vec{a}+\vec{b})$ and $(\vec{a}-\vec{b})$, where $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \quad \vec{b}=\hat{i}+2 \hat{j}+3 \hat{k}$.

Solution We have $\vec{a}+\vec{b}=2 \hat{i}+3 \hat{j}+4 \hat{k}$ and $\vec{a}-\vec{b}=-\hat{j}-2 \hat{k}$

A vector which is perpendicular to both $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ is given by

Now $$ (\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 0 & -1 & -2 \end{vmatrix} =-2 \hat{i}+4 \hat{j}-2 \hat{k} \quad(=\vec{c}, \text{ say }) $$

$$ |\vec{c}|=\sqrt{4+16+4}=\sqrt{24}=2 \sqrt{6} $$

Therefore, the required unit vector is $$ \frac{\vec{c}}{|\vec{c}|}=\frac{-1}{\sqrt{6}} \hat{i}+\frac{2}{\sqrt{6}} \hat{j}-\frac{1}{\sqrt{6}} \hat{k} $$

Note There are two perpendicular directions to any plane. Thus, another unit vector perpendicular to $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ will be $\frac{1}{\sqrt{6}} \hat{i}-\frac{2}{\sqrt{6}} \hat{j}+\frac{1}{\sqrt{6}} \hat{k}$. But that will be a consequence of $(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$.

Example 24 Find the area of a triangle having the points $A(1,1,1), B(1,2,3)$ and $C(2,3,1)$ as its vertices.

Solution We have $\overrightarrow{{}AB}=\hat{j}+2 \hat{k}$ and $\overrightarrow{{}AC}=\hat{i}+2 \hat{j}$. The area of the given triangle is $\frac{1}{2}|\overrightarrow{{}AB} \times \overrightarrow{{}AC}|$.

Now, $$ \overrightarrow{{}AB} \times \overrightarrow{{}AC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{vmatrix} =-4 \hat{i}+2 \hat{j}-\hat{k} $$

Therefore $$ |\overrightarrow{{}AB} \times \overrightarrow{{}AC}|=\sqrt{16+4+1}=\sqrt{21} $$

Thus, the required area is $\frac{1}{2} \sqrt{21}$

Example 25 Find the area of a parallelogram whose adjacent sides are given by the vectors $\vec{a}=3 \hat{i}+\hat{j}+4 \hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+\hat{k}$

Solution The area of a parallelogram with $\vec{a}$ and $\vec{b}$ as its adjacent sides is given by $|\vec{a} \times \vec{b}|$.

Now $$ \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 4 \\ 1 & -1 & 1 \end{vmatrix} =5 \hat{i}+\hat{j}-4 \hat{k} $$

Therefore $$ |\vec{a} \times \vec{b}|=\sqrt{25+1+16}=\sqrt{42} $$

and hence, the required area is $\sqrt{42}$.

EXERCISE 10.4

1. Find $|\vec{a} \times \vec{b}|$, if $\vec{a}=\hat{i}-7 \hat{j}+7 \hat{k}$ and $\vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k}$.

Show Answer

Solution

We have,

$ \begin{aligned} & \vec{a}=\hat{i}-7 \hat{j}+7 \hat{k} \text{ and } \vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k} \\ & \begin{aligned} \vec{a} \times \vec{b} & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -7 & 7 \\ 3 & -2 & 2 \end{vmatrix} \\ & =\hat{i}(-14+14)-\hat{j}(2-21)+\hat{k}(-2+21)=19 \hat{j}+19 \hat{k} \end{aligned} \\ & \therefore|\vec{a} \times \vec{b}|=\sqrt{(19)^{2}+(19)^{2}}=\sqrt{2 \times(19)^{2}}=19 \sqrt{2} \end{aligned} $

2. Find a unit vector perpendicular to each of the vector $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$, where $\vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k}$ and $\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}$.

Show Answer

Solution

We have,

$ \begin{aligned} & \vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k} \text{ and } \vec{b}=\hat{i}+2 \hat{j}-2 \hat{k} \\ & \therefore \vec{a}+\vec{b}=4 \hat{i}+4 \hat{j}, \vec{a}-\vec{b}=2 \hat{i}+4 \hat{k} \\ & (\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 4 & 0 \\ 2 & 0 & 4 \end{vmatrix} =\hat{i}(16)-\hat{j}(16)+\hat{k}(-8)=16 \hat{i}-16 \hat{j}-8 \hat{k} \\ & \therefore|(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|=\sqrt{16^{2}+(-16)^{2}+(-8)^{2}} \\ & =\sqrt{2^{2} \times 8^{2}+2^{2} \times 8^{2}+8^{2}} \\ & =8 \sqrt{2^{2}+2^{2}+1}=8 \sqrt{9}=8 \times 3=24 \end{aligned} $

Hence, the unit vector perpendicular to each of the vectors $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ is given by the relation,

$= \pm \frac{(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})}{|(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|}= \pm \frac{16 \hat{i}-16 \hat{j}-8 \hat{k}}{24}$

$= \pm \frac{2 \hat{i}-2 \hat{j}-\hat{k}}{3}= \pm \frac{2}{3} \hat{i} \mp \frac{2}{3} \hat{j} \mp \frac{1}{3} \hat{k}$

3. If a unit vector $\vec{a}$ makes angles $\frac{\pi}{3}$ with $\hat{i}, \frac{\pi}{4}$ with $\hat{j}$ and an acute angle $\theta$ with $\hat{k}$, then find $\theta$ and hence, the components of $\vec{a}$.

Show Answer

Solution

Let unit vector $\vec{a}$ have ( $.a_1, a_2, a_3)$ components.

$ \vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k} $

Since $\vec{a}$ is a unit vector, $|\vec{a}|=1$.

Also, it is given that $\vec{a}$ makes angles $\frac{\pi}{3}$ with $\hat{i}, \frac{\pi}{4}$ with $\hat{j}$, and an acute angle $\theta$ with $\hat{k}$. Then, we have:

$\cos \frac{\pi}{3}=\frac{a_1}{|\vec{a}|}$

$\Rightarrow \frac{1}{2}=a_1 \quad[|\vec{a}|=1]$

$\cos \frac{\pi}{4}=\frac{a_2}{|\vec{a}|}$

$\Rightarrow \frac{1}{\sqrt{2}}=a_2 \quad[|\vec{a}|=1]$

Also, $\cos \theta=\frac{a_3}{|\vec{a}|}$.

$\Rightarrow a_3=\cos \theta$

Now,

$|a|=1$

$\Rightarrow \sqrt{a_1^{2}+a_2^{2}+a_3^{2}}=1$

$\Rightarrow(\frac{1}{2})^{2}+(\frac{1}{\sqrt{2}})^{2}+\cos ^{2} \theta=1$

$\Rightarrow \frac{1}{4}+\frac{1}{2}+\cos ^{2} \theta=1$

$\Rightarrow \frac{3}{4}+\cos ^{2} \theta=1$

$\Rightarrow \cos ^{2} \theta=1-\frac{3}{4}=\frac{1}{4}$

$\Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{3}$

$\therefore a_3=\cos \frac{\pi}{3}=\frac{1}{2}$

Hence, $\theta=\frac{\pi}{3}$ and the components of $\vec{a}$ are $(\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2})$.

4. Show that

$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})$

Show Answer

Solution

$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$

$=(\vec{a}-\vec{b}) \times \vec{a}+(\vec{a}-\vec{b}) \times \vec{b} \quad$ [By distributivity of vector product over addition]

$=\vec{a} \times \vec{a}-\vec{b} \times \vec{a}+\vec{a} \times \vec{b}-\vec{b} \times \vec{b} \quad$ [Again, by distributivity of vector product over addition]

$=\overrightarrow{{}0}+\vec{a} \times \vec{b}+\vec{a} \times \vec{b}-\overrightarrow{{}0}$

$=2 (\vec{a} \times \vec{b})$

5. Find $\lambda$ and $\mu$ if $(2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{{}0}$.

Show Answer

Solution

$(2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{{}0}$

$\Rightarrow \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 6 & 27 \\ 1 & \lambda & \mu\end{vmatrix} =0 \hat{i}+0 \hat{j}+0 \hat{k}$

$\Rightarrow \hat{i}(6 \mu-27 \lambda)-\hat{j}(2 \mu-27)+\hat{k}(2 \lambda-6)=0 \hat{i}+0 \hat{j}+0 \hat{k}$

On comparing the corresponding components, we have:

$6 \mu-27 \lambda=0$

$2 \mu-27=0$

$2 \lambda-6=0$

Now,

$2 \lambda-6=0 \Rightarrow \lambda=3$

$2 \mu-27=0 \Rightarrow \mu=\frac{27}{2}$

Hence, $\lambda=3$ and $\mu=\frac{27}{2}$.

6. Given that $\vec{a} \cdot \vec{b}=0$ and $\vec{a} \times \vec{b}=\overrightarrow{{}0}$. What can you conclude about the vectors $\vec{a}$ and $\vec{b}$ ?

Show Answer

Solution

$\vec{a} \cdot \vec{b}=0$

Then,

(i) Either $|\vec{a}|=0$ or $|\vec{b}|=0$, or $\vec{a} \perp \vec{b}$ (in case $\vec{a}$ and $\vec{b}$ are non-zero)

$\vec{a} \times \vec{b}=0$

(ii) Either $|\vec{a}|=0$ or $|\vec{b}|=0$, or $\vec{a} | \vec{b}$ (in case $\vec{a}$ and $\vec{b}$ are non-zero)

But, $\vec{a}$ and $\vec{b}$ cannot be perpendicular and parallel simultaneously.

Hence, $|\vec{a}|=0$ or $|\vec{b}|=0$.

7. Let the vectors $\vec{a}, \vec{b}, \vec{c}$ be given as $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, $c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$. Then show that $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$.

Show Answer

Solution

We have,

$\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, \vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}, \vec{c}=c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$

$(\vec{b}+\vec{c})=(b_1+c_1) \hat{i}+(b_2+c_2) \hat{j}+(b_3+c_3) \hat{k}$

Now, $\vec{a} \times(\vec{b}+\vec{c}) \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1+c_1 & b_2+c_2 & b_3+c_3\end{vmatrix} $

$=\hat{i}[a_2(b_3+c_3)-a_3(b_2+c_2)]-\hat{j}[a_1(b_3+c_3)-a_3(b_1+c_1)]+\hat{k}[a_1(b_2+c_2)-a_2(b_1+c_1)]$

$=\hat{i}[a_2 b_3+a_2 c_3-a_3 b_2-a_3 c_2]+\hat{j}[-a_1 b_3-a_1 c_3+a_3 b_1+a_3 c_1]+\hat{k}[a_1 b_2+a_1 c_2-a_2 b_1-a_2 c_1]$

$\vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{vmatrix} $

$=\hat{i}[a_2 b_3-a_3 b_2]+\hat{j}[b_1 a_3-a_1 b_3]+\hat{k}[a_1 b_2-a_2 b_1]$

$\vec{a} \times \vec{c}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3\end{vmatrix} $

$$ \begin{equation*} =\hat{i}[a_2 c_3-a_3 c_2]+\hat{j}[a_3 c_1-a_1 c_3]+\hat{k}[a_1 c_2-a_2 c_1] \tag{3} \end{equation*} $$

On adding (2) and (3), we get:

$(\vec{a} \times \vec{b})+(\vec{a} \times \vec{c})=\hat{i}[a_2 b_3+a_2 c_3-a_3 b_2-a_3 c_2]+\hat{j}[b_1 a_3+a_3 c_1-a_1 b_3-a_1 c_3]$

$+\hat{k}[a_1 b_2+a_1 c_2-a_2 b_1-a_2 c_1]$

Now, from (1) and (4), we have:

$\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

Hence, the given result is proved.

8. If either $\vec{a}=\overrightarrow{{}0}$ or $\vec{b}=\overrightarrow{{}0}$, then $\vec{a} \times \vec{b}=\overrightarrow{{}0}$. Is the converse true? Justify your answer with an example.

Show Answer

Solution

Take any parallel non-zero vectors so that $\vec{a} \times \vec{b}=\overrightarrow{{}0}$.

Let $\vec{a}=2 \hat{i}+3 \hat{j}+4 \hat{k}, \vec{b}=4 \hat{i}+6 \hat{j}+8 \hat{k}$.

Then,

$\vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 4 & 6 & 8\end{vmatrix} =\hat{i}(24-24)-\hat{j}(16-16)+\hat{k}(12-12)=0 \hat{i}+0 \hat{j}+0 \hat{k}=\overrightarrow{{}0}$

It can now be observed that:

$|\vec{a}|=\sqrt{2^{2}+3^{2}+4^{2}}=\sqrt{29}$

$\therefore \vec{a} \neq \overrightarrow{{}0}$

$|\vec{b}|=\sqrt{4^{2}+6^{2}+8^{2}}=\sqrt{116}$

$\therefore \vec{b} \neq \overrightarrow{{}0}$

Hence, the converse of the given statement need not be true.

9. Find the area of the triangle with vertices $A(1,1,2), B(2,3,5)$ and $C(1,5,5)$.

Show Answer

Solution

The vertices of triangle $A B C$ are given as $A(1,1,2), B(2,3,5)$, and $C(1,5,5)$.

The adjacent sides $\overrightarrow{{}AB}$ and $\overrightarrow{{}BC}$ of $\triangle ABC$ are given as:

$ \begin{aligned} & \overrightarrow{{}AB}=(2-1) \hat{i}+(3-1) \hat{j}+(5-2) \hat{k}=\hat{i}+2 \hat{j}+3 \hat{k} \\ & \overrightarrow{{}BC}=(1-2) \hat{i}+(5-3) \hat{j}+(5-5) \hat{k}=-\hat{i}+2 \hat{j} \end{aligned} $

Area of $\triangle ABC=\frac{1}{2}|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|$

$\overrightarrow{{}AB} \times \overrightarrow{{}BC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ -1 & 2 & 0\end{vmatrix} =\hat{i}(-6)-\hat{j}(3)+\hat{k}(2+2)=-6 \hat{i}-3 \hat{j}+4 \hat{k}$

$\therefore|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|=\sqrt{(-6)^{2}+(-3)^{2}+4^{2}}=\sqrt{36+9+16}=\sqrt{61}$

Hence, the area of $\triangle A B C$ is $\frac{\sqrt{61}}{2}$ square units.

10. Find the area of the parallelogram whose adjacent sides are determined by the vectors $\vec{a}=\hat{i}-\hat{j}+3 \hat{k}$ and $\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}$.

Show Answer

Solution

The area of the parallelogram whose adjacent sides are $\vec{a}$ and $\vec{b}$ is $|\vec{a} \times \vec{b}|$.

Adjacent sides are given as:

$\vec{a}=\hat{i}-\hat{j}+3 \hat{k}$ and $\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}$

$\therefore \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 3 \\ 2 & -7 & 1\end{vmatrix} =\hat{i}(-1+21)-\hat{j}(1-6)+\hat{k}(-7+2)=20 \hat{i}+5 \hat{j}-5 \hat{k}$

$|\vec{a} \times \vec{b}|=\sqrt{20^{2}+5^{2}+5^{2}}=\sqrt{400+25+25}=15 \sqrt{2}$

Hence, the area of the given parallelogram is $15 \sqrt{2}$ square units .

11. Let the vectors $\vec{a}$ and $\vec{b}$ be such that $|\vec{a}|=3$ and $|\vec{b}|=\frac{\sqrt{2}}{3}$, then $\vec{a} \times \vec{b}$ is a unit vector, if the angle between $\vec{a}$ and $\vec{b}$ is

(A) $\pi / 6$

(B) $\pi / 4$

(C) $\pi / 3$

(D) $\pi / 2$

Show Answer

Solution

It is given that $|\vec{a}|=3$ and $|\vec{b}|=\frac{\sqrt{2}}{3}$.

We know that $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n}$, where $\hat{n}$ is a unit vector perpendicular to both $\vec{a}$ and $\vec{b}$ and $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.

Now, $\vec{a} \times \vec{b}$ is a unit vector if $|\vec{a} \times \vec{b}|=1$.

$|\vec{a} \times \vec{b}|=1$

$\Rightarrow|| \vec{a}|| \vec{b}|\sin \theta \hat{n}|=1$

$\Rightarrow|\vec{a}||\vec{b}||\sin \theta|=1$

$\Rightarrow 3 \times \frac{\sqrt{2}}{3} \times \sin \theta=1$

$\Rightarrow \sin \theta=\frac{1}{\sqrt{2}}$

$\Rightarrow \theta=\frac{\pi}{4}$

Hence, $\vec{a} \times \vec{b}$ is a unit vector if the angle between $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$.

The correct answer is $B$.

12. Area of a rectangle having vertices $A, B, C$ and $D$ with position vectors $-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$ and $-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$, respectively is

(A) $\frac{1}{2}$

(B) 1

(C) 2

(D) 4

Show Answer

Solution

The position vectors of vertices $A, B, C$, and $D$ of rectangle $A B C D$ are given as:

$\overrightarrow{{}OA}=-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OB}=\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OC}=\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OD}=-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$

The adjacent sides $\overrightarrow{{}AB}$ and $\overrightarrow{{}BC}$ of the given rectangle are given as:

$ \begin{aligned} & \overrightarrow{{}AB}=(1+1) \hat{i}+(\frac{1}{2}-\frac{1}{2}) \hat{j}+(4-4) \hat{k}=2 \hat{i} \\ & \overrightarrow{{}BC}=(1-1) \hat{i}+(-\frac{1}{2}-\frac{1}{2}) \hat{j}+(4-4) \hat{k}=-\hat{j} \\ & \therefore \overrightarrow{{}AB} \times \overrightarrow{{}BC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 0 & 0 \\ 0 & -1 & 0 \end{vmatrix} =\hat{k}(-2)=-2 \hat{k} \\ & |\overrightarrow{{}AB} \times \overrightarrow{{}AC}|=\sqrt{(-2)^{2}}=2 \end{aligned} $

Now, it is known that the area of a parallelogram whose adjacent sides are $\vec{a}$ and $\vec{b}$ is $|\vec{a} \times \vec{b}|$.

Hence, the area of the given rectangle is $|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|=2$ square units. The correct answer is $C$.

Miscellaneous Examples

Example 26 Write all the unit vectors in XY-plane.

Solution Let $\vec{r}=x \hat{i}+y \hat{j}$ be a unit vector in XY-plane (Fig 10.28). Then, from the figure, we have $x=\cos \theta$ and $y=\sin \theta($ since $|\vec{r}|=1)$. So, we may write the vector $\vec{r}$ as

$$ \vec{r}(=\overrightarrow{{}OP})=\cos \theta \hat{i}+\sin \theta \hat{j} $$

Clearly, $$ |\vec{r}|=\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}=1 $$

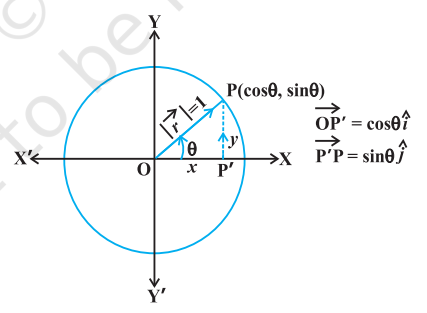
Fig 10.28

Also, as $\theta$ varies from 0 to $2 \pi$, the point $P$ (Fig 10.28) traces the circle $x^{2}+y^{2}=1$ counterclockwise, and this covers all possible directions. So, (1) gives every unit vector in the XY-plane.

Example 27 If $\hat{i}+\hat{j}+\hat{k}, 2 \hat{i}+5 \hat{j}, 3 \hat{i}+2 \hat{j}-3 \hat{k}$ and $\hat{i}-6 \hat{j}-\hat{k}$ are the position vectors of points $A, B, C$ and $D$ respectively, then find the angle between $\overrightarrow{{}A B}$ and $\overrightarrow{{}C D}$. Deduce that $\overrightarrow{{}AB}$ and $\overrightarrow{{}CD}$ are collinear.

Solution Note that if $\theta$ is the angle between $A B$ and $C D$, then $\theta$ is also the angle between $\overrightarrow{{}AB}$ and $\overrightarrow{{}CD}$.

Now $$ \begin{aligned} \overrightarrow{{}AB} & =\text{ Position vector of } B-\text{ Position vector of } A \\ & =(2 \hat{i}+5 \hat{j})-(\hat{i}+\hat{j}+\hat{k})=\hat{i}+4 \hat{j}-\hat{k} \end{aligned} $$

Therefore $$ |\overrightarrow{{}AB}|=\sqrt{(1)^{2}+(4)^{2}+(-1)^{2}}=3 \sqrt{2} $$

Similarly $ \overrightarrow{{}CD}=-2 \hat{i}-8 \hat{j}+2 \hat{k} \text{ and }|\overrightarrow{{}CD}|=6 \sqrt{2} $

Thus $$ \begin{aligned} \cos \theta & =\frac{\overrightarrow{{}AB} \cdot \overrightarrow{{}CD}}{|\overrightarrow{{}AB}||\overrightarrow{{}CD}|} \\ & =\frac{1(-2)+4(-8)+(-1)(2)}{(3 \sqrt{2})(6 \sqrt{2})}=\frac{-36}{36}=-1 \end{aligned} $$

Since $0 \leq \theta \leq \pi$, it follows that $\theta=\pi$. This shows that $\overrightarrow{{}A B}$ and $\overrightarrow{{}C D}$ are collinear.

Alternatively, $\overrightarrow{{}AB}=-\frac{1}{2} \overrightarrow{{}CD}$ which implies that $\overrightarrow{{}AB}$ and $\overrightarrow{{}CD}$ are collinear vectors.

Example 28 Let $\vec{a}, \vec{b}$ and $\vec{c}$ be three vectors such that $|\vec{a}|=3,|\vec{b}|=4,|\vec{c}|=5$ and each one of them being perpendicular to the sum of the other two, find $|\vec{a}+\vec{b}+\vec{c}|$.

Solution Given $\vec{a} \cdot(\vec{b}+\vec{c})=0, \vec{b} \cdot(\vec{c}+\vec{a})=0, \vec{c} \cdot(\vec{a}+\vec{b})=0$.

Now $$ \begin{aligned} |\vec{a}+\vec{b}+\vec{c}|^{2}= & (\vec{a}+\vec{b}+\vec{c})^{2}=(\vec{a}+\vec{b}+\vec{c}) \cdot(\vec{a}+\vec{b}+\vec{c}) \\ = & \vec{a} \cdot \vec{a}+\vec{a} \cdot(\vec{b}+\vec{c})+\vec{b} \cdot \vec{b}+\vec{b} \cdot(\vec{a}+\vec{c}) \\ & +\vec{c} \cdot(\vec{a}+\vec{b})+\vec{c} \cdot \vec{c} \\ = & |\vec{a}|^{2}+|\vec{b}|^{2}+|\vec{c}|^{2} \\ = & 9+16+25=50 \end{aligned} $$

Therefore $$ |\vec{a}+\vec{b}+\vec{c}|=\sqrt{50}=5 \sqrt{2} $$

Example 29 Three vectors $\vec{a}, \vec{b}$ and $\vec{c}$ satisfy the condition $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$. Evaluate the quantity $\mu=\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$, if $|\vec{a}|=3,|\vec{b}|=4$ and $|\vec{c}|=2$.

Solution Since $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$, we have

or $$ \begin{matrix} \vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}=0 \\ \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}=0 \end{matrix} $$ $$ \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}=-|\vec{a}|^{2}=-9 $$ $$ \vec{b} \cdot(\vec{a}+\vec{b}+\vec{c})=0 $$ $$ \vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}=-|\vec{b}|^{2}=-16 $$

Similarly $$ \vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}=-4 $$

Adding (1), (2) and (3), we have $$ \begin{matrix} 2(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{a} \cdot \vec{c})=-29 \\ 2 \mu=-29, \text{ i.e., } \mu=\frac{-29}{2} \end{matrix} $$

Example 30 If with reference to the right handed system of mutually perpendicular unit vectors $ \hat {i}, \hat {j} $ and $ \hat {k}, \vec{\alpha}=3 \hat {i} - \hat {j}, \vec{\beta}=2 \hat {i} + \hat {j} - 3 \hat {k} $ , then express $ \vec{\beta} $ in the form $ \vec{\beta}=\vec{\beta} _ {1} + \vec{\beta} _ {2} $, where $ \vec{\beta} _ {1} $ is parallel to $ \vec{\alpha} $ and $ \vec{\beta} _ {2} $ is perpendicular to $\vec{\alpha} $.

Solution Let $ \vec{\beta} _ {1} =\lambda \vec{\alpha}, \lambda $ is a scalar, i.e., $ \vec{\beta} _ {1} = 3 \lambda \hat {i} - \lambda \hat {j} $.

Now $$ \vec{\beta} _ {2}=\vec{\beta}-\vec{\beta} _ {1}=(2-3 \lambda) \hat{i}+(1+\lambda) \hat{j}-3 \hat{k} $$

Now, since $\vec{\beta} _ {2}$ is to be perpendicular to $\vec{\alpha}$, we should have $\vec{\alpha} \cdot \vec{\beta} _ {2}=0$. i.e.,

or $$ 3(2-3 \lambda)-(1+\lambda)=0 $$

or $$ \lambda=\frac{1}{2} $$

therefore $$ \vec{\beta} _{1}=\frac{3}{2} \hat{i}-\frac{1}{2} \hat{j} \text { और } \quad \vec{\beta} _{2}=\frac{1}{2} \hat{i}+\frac{3}{2} \hat{j}-3 \hat{k} $$

Miscellaneous Exercise on Chapter 10

1. Write down a unit vector in XY-plane, making an angle of $30^{\circ}$ with the positive direction of $x$-axis.

Show Answer

Solution

If $\vec{r}$ is a unit vector in the $X Y$-plane, then $\vec{r}=\cos \theta \hat{i}+\sin \theta \hat{j}$.

Here, $\theta$ is the angle made by the unit vector with the positive direction of the $x$-axis.

Therefore, for $\theta=30^{\circ}$ :

$\vec{r}=\cos 30^{\circ} \hat{i}+\sin 30^{\circ} \hat{j}=\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}$

Hence, the required unit vector is $\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}$

2. Find the scalar components and magnitude of the vector joining the points $P(x _ {1}, y _ {1}, z _ {1})$ and $Q(x _ {2}, y _ {2}, z _ {2})$.

Show Answer

Solution

The vector joining the points $P(x_1, y_1, z_1)$ and $Q(x_2, y_2, z_2)$ can be obtained by, $\overrightarrow{{}PQ}=$ Position vector of $Q-$ Position vector of $P$

$ =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} $

$ |\overrightarrow{{}PQ}|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $

Hence, the scalar components and the magnitude of the vector joining the given points

are respectively ${(x_2-x_1),(y_2-y_1),(z_2-z_1)}$ and $\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}}$.

3. A girl walks $4 km$ towards west, then she walks $3 km$ in a direction $30^{\circ}$ east of north and stops. Determine the girl’s displacement from her initial point of departure.

Show Answer

Solution

Let $O$ and $B$ be the initial and final positions of the girl respectively. Then, the girl’s position can be shown as:

Now, we have:

$ \begin{aligned} \overrightarrow{{}OA} & =-4 \hat{i} \\ \overrightarrow{{}AB} & =\hat{i}|\overrightarrow{{}AB}| \cos 60^{\circ}+\hat{j}|\overrightarrow{{}AB}| \sin 60^{\circ} \\ & =\hat{i} 3 \times \frac{1}{2}+\hat{j} 3 \times \frac{\sqrt{3}}{2} \\ & =\frac{3}{2} \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j} \end{aligned} $

By the triangle law of vector addition, we have:

$ \begin{aligned} \overrightarrow{{}OB} & =\overrightarrow{{}OA}+\overrightarrow{{}AB} \\ & =(-4 \hat{i})+(\frac{3}{2} \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j}) \\ & =(-4+\frac{3}{2}) \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j} \\ & =(\frac{-8+3}{2}) \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j} \\ & =\frac{-5}{2} \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j} \end{aligned} $

Hence, the girl’s displacement from her initial point of departure is

$ \frac{-5}{2} \hat{i}+\frac{3 \sqrt{3}}{2} \hat{j} $

4. If $\vec{a}=\vec{b}+\vec{c}$, then is it true that $|\vec{a}|=|\vec{b}|+|\vec{c}|$ ? Justify your answer.

Show Answer

Solution

In $\triangle ABC$, let $\overrightarrow{{}CB}=\vec{a}, \overrightarrow{{}CA}=\vec{b}$, and $\overrightarrow{{}AB}=\vec{c}$ (as shown in the following figure).

Now, by the triangle law of vector addition, we have $\vec{a}=\vec{b}+\vec{c}$.

It is clearly known that $|\vec{a}|,|\vec{b}|$, and $|\vec{c}|$ represent the sides of $\triangle ABC$.

Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side.

$\therefore|\vec{a}|<|\vec{b}|+|\vec{c}|$

Hence, it is not true that $|\vec{a}|=|\vec{b}|+|\vec{c}|$.

5. Find the value of $x$ for which $x(\hat{i}+\hat{j}+\hat{k})$ is a unit vector.

Show Answer

Solution

$x(\hat{i}+\hat{j}+\hat{k})$ is a unit vector if $|x(\hat{i}+\hat{j}+\hat{k})|=1$.

Now,

$|x(\hat{i}+\hat{j}+\hat{k})|=1$

$\Rightarrow \sqrt{x^{2}+x^{2}+x^{2}}=1$

$\Rightarrow \sqrt{3 x^{2}}=1$

$\Rightarrow \sqrt{3} x=1$

$\Rightarrow x= \pm \frac{1}{\sqrt{3}}$

Hence, the required value of $x$ is $\pm \frac{1}{\sqrt{3}}$.

6. Find a vector of magnitude 5 units, and parallel to the resultant of the vectors $\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}$ and $\vec{b}=\hat{i}-2 \hat{j}+\hat{k}$.

Show Answer

Solution

We have,

$\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}$ and $\vec{b}=\hat{i}-2 \hat{j}+\hat{k}$

Let $\vec{c}$ be the resultant of $\vec{a}$ and $\vec{b}$.

Then,

$\vec{c}=\vec{a}+\vec{b}=(2+1) \hat{i}+(3-2) \hat{j}+(-1+1) \hat{k}=3 \hat{i}+\hat{j}$

$\therefore|\vec{c}|=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10}$

$\therefore \hat{c}=\frac{\vec{c}}{|\vec{c}|}=\frac{(3 \hat{i}+\hat{j})}{\sqrt{10}}$

Hence, the vector of magnitude 5 units and parallel to the resultant of vectors $\vec{a}$ and $\vec{b}$ is

$\pm 5 \cdot \hat{c}= \pm 5 \cdot \frac{1}{\sqrt{10}}(3 \hat{i}+\hat{j})= \pm \frac{3 \sqrt{10} \hat{i}}{2} \pm \frac{\sqrt{10}}{2} \hat{j}$.

7. If $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k}$ and $\vec{c}=\hat{i}-2 \hat{j}+\hat{k}$, find a unit vector parallel to the vector $2 \vec{a}-\vec{b}+3 \vec{c}$.

Show Answer

Solution

We have,

$ \begin{aligned} & \vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k} \text{ and } \vec{c}=\hat{i}-2 \hat{j}+\hat{k} \\ & \begin{aligned} 2 \vec{a}-\vec{b}+3 \vec{c} & =2(\hat{i}+\hat{j}+\hat{k})-(2 \hat{i}-\hat{j}+3 \hat{k})+3(\hat{i}-2 \hat{j}+\hat{k}) \\ & =2 \hat{i}+2 \hat{j}+2 \hat{k}-2 \hat{i}+\hat{j}-3 \hat{k}+3 \hat{i}-6 \hat{j}+3 \hat{k} \\ & =3 \hat{i}-3 \hat{j}+2 \hat{k} \end{aligned} \\ & \begin{aligned} |2 \vec{a}-\vec{b}+3 \vec{c}| & =\sqrt{3^{2}+(-3)^{2}+2^{2}}=\sqrt{9+9+4}=\sqrt{22} \end{aligned} \end{aligned} $

Hence, the unit vector along $2 \vec{a}-\vec{b}+3 \vec{c}$ is

$ \frac{2 \vec{a}-\vec{b}+3 \vec{c}}{|2 \vec{a}-\vec{b}+3 \vec{c}|}=\frac{3 \hat{i}-3 \hat{j}+2 \hat{k}}{\sqrt{22}}=\frac{3}{\sqrt{22}} \hat{i}-\frac{3}{\sqrt{22}} \hat{j}+\frac{2}{\sqrt{22}} \hat{k} $

8. Show that the points $A(1,-2,-8), B(5,0,-2)$ and $C(11,3,7)$ are collinear, and find the ratio in which $B$ divides $AC$.

Show Answer

Solution

The given points are $A(1,-2,-8), B(5,0,-2)$, and $C(11,3,7)$.

$\therefore \overrightarrow{{}AB}=(5-1) \hat{i}+(0+2) \hat{j}+(-2+8) \hat{k}=4 \hat{i}+2 \hat{j}+6 \hat{k}$

$ \overrightarrow{{}BC}=(11-5) \hat{i}+(3-0) \hat{j}+(7+2) \hat{k}=6 \hat{i}+3 \hat{j}+9 \hat{k} $

$\overrightarrow{{}AC}=(11-1) \hat{i}+(3+2) \hat{j}+(7+8) \hat{k}=10 \hat{i}+5 \hat{j}+15 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{4^{2}+2^{2}+6^{2}}=\sqrt{16+4+36}=\sqrt{56}=2 \sqrt{14}$

$|\overrightarrow{{}BC}|=\sqrt{6^{2}+3^{2}+9^{2}}=\sqrt{36+9+81}=\sqrt{126}=3 \sqrt{14}$

$|\overrightarrow{{}AC}|=\sqrt{10^{2}+5^{2}+15^{2}}=\sqrt{100+25+225}=\sqrt{350}=5 \sqrt{14}$

$\therefore|\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}|$

Thus, the given points $A, B$, and $C$ are collinear.

Now, let point $B$ divide $AC$ in the ratio $\lambda: 1$. Then, we have:

$ \begin{aligned} & \overrightarrow{{}OB}=\frac{\lambda \overrightarrow{{}OC}+\overrightarrow{{}OA}}{(\lambda+1)} \\ & \Rightarrow 5 \hat{i}-2 \hat{k}=\frac{\lambda(11 \hat{i}+3 \hat{j}+7 \hat{k})+(\hat{i}-2 \hat{j}-8 \hat{k})}{\lambda+1} \\ & \Rightarrow(\lambda+1)(5 \hat{i}-2 \hat{k})=11 \lambda \hat{i}+3 \lambda \hat{j}+7 \lambda \hat{k}+\hat{i}-2 \hat{j}-8 \hat{k} \\ & \Rightarrow 5(\lambda+1) \hat{i}-2(\lambda+1) \hat{k}=(11 \lambda+1) \hat{i}+(3 \lambda-2) \hat{j}+(7 \lambda-8) \hat{k} \end{aligned} $

On equating the corresponding components, we get:

$5(\lambda+1)=11 \lambda+1$

$\Rightarrow 5 \lambda+5=11 \lambda+1$

$\Rightarrow 6 \lambda=4$

$\Rightarrow \lambda=\frac{4}{6}=\frac{2}{3}$

Hence, point $B$ divides $A C$ in the ratio $2: 3$.

9. Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$ whose position vectors are $(2 \vec{a}+\vec{b})$ and $(\vec{a}-3 \vec{b})$ externally in the ratio $1: 2$. Also, show that $P$ is the mid point of the line segment RQ.

Show Answer

Solution

It is given that $\overrightarrow{{}OP}=2 \vec{a}+\vec{b}, \overrightarrow{{}OQ}=\vec{a}-3 \vec{b}$.

It is given that point $R$ divides a line segment joining two points $P$ and $Q$ externally in the ratio $1: 2$. Then, on using the section formula, we get:

$\overrightarrow{{}OR}=\frac{2(2 \vec{a}+\vec{b})-(\vec{a}-3 \vec{b})}{2-1}=\frac{4 \vec{a}+2 \vec{b}-\vec{a}+3 \vec{b}}{1}=3 \vec{a}+5 \vec{b}$

Therefore, the position vector of point $R$ is $3 \vec{a}+5 \vec{b}$.

Position vector of the mid-point of $RQ=\frac{\overrightarrow{{}OQ}+\overrightarrow{{}OR}}{2}$ $=\frac{(\vec{a}-3 \vec{b})+(3 \vec{a}+5 \vec{b})}{2}$

$=2 \vec{a}+\vec{b}$

$=\overrightarrow{{}OP}$

Hence, $P$ is the mid-point of the line segment $R Q$.

10. The two adjacent sides of a parallelogram are $2 \hat{i}-4 \hat{j}+5 \hat{k}$ and $\hat{i}-2 \hat{j}-3 \hat{k}$. Find the unit vector parallel to its diagonal. Also, find its area.

Show Answer

Solution

Adjacent sides of a parallelogram are given as: $\vec{a}=2 \hat{i}-4 \hat{j}+5 \hat{k}$ and $\vec{b}=\hat{i}-2 \hat{j}-3 \hat{k}$

Then, the diagonal of a parallelogram is given by $\vec{a}+\vec{b}$.

$\vec{a}+\vec{b}=(2+1) \hat{i}+(-4-2) \hat{j}+(5-3) \hat{k}=3 \hat{i}-6 \hat{j}+2 \hat{k}$

Thus, the unit vector parallel to the diagonal is

$ \frac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|}=\frac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{\sqrt{3^{2}+(-6)^{2}+2^{2}}}=\frac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{\sqrt{9+36+4}}=\frac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{7}=\frac{3}{7} \hat{i}-\frac{6}{7} \hat{j}+\frac{2}{7} \hat{k} . $

$\therefore$ Area of parallelogram $ABCD=|\vec{a} \times \vec{b}|$

$ \begin{aligned} & \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 5 \\ 1 & -2 & -3 \end{vmatrix} \\ &=\hat{i}(12+10)-\hat{j}(-6-5)+\hat{k}(-4+4) \\ &=22 \hat{i}+11 \hat{j} \\ &=11(2 \hat{i}+\hat{j}) \\ & \therefore|\vec{a} \times \vec{b}|=11 \sqrt{2^{2}+1^{2}}=11 \sqrt{5} \end{aligned} $

Hence, the area of the parallelogram is $11 \sqrt{5}$ square units.

11. Show that the direction cosines of a vector equally inclined to the axes $OX, OY$ and $OZ$ are $\pm(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$.

Show Answer

Solution

Let a vector be equally inclined to axes OX, OY, and OZ at angle $a$.

Then, the direction cosines of the vector are $\cos a, \cos a$, and $\cos a$.

Now,

$\cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1$

$\Rightarrow 3 \cos ^{2} \alpha=1$

$\Rightarrow \cos \alpha=\frac{1}{\sqrt{3}}$

Hence, the direction cosines of the vector which are equally inclined to the axes

are $\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}$.

12. Let $\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}, \vec{b}=3 \hat{i}-2 \hat{j}+7 \hat{k}$ and $\vec{c}=2 \hat{i}-\hat{j}+4 \hat{k}$. Find a vector $\vec{d}$ which is perpendicular to both $\vec{a}$ and $\vec{b}$, and $\vec{c} \cdot \vec{d}=15$.

Show Answer

Solution

Let $\vec{d}=d_1 \hat{i}+d_2 \hat{j}+d_3 \hat{k}$.

Since $\vec{d}$ is perpendicular to both $\vec{a}$ and $\vec{b}$, we have:

$\vec{d} \cdot \vec{a}=0$

$\Rightarrow d_1+4 d_2+2 d_3=0$

And,

$\vec{d} \cdot \vec{b}=0$

$\Rightarrow 3 d_1-2 d_2+7 d_3=0$

Also, it is given that:

$\vec{c} \cdot \vec{d}=15$

$\Rightarrow 2 d_1-d_2+4 d_3=15$

On solving (i), (ii), and (iii), we get:

$d_1=\frac{160}{3}, d_2=-\frac{5}{3}$ and $d_3=-\frac{70}{3}$

$\therefore \vec{d}=\frac{160}{3} \hat{i}-\frac{5}{3} \hat{j}-\frac{70}{3} \hat{k}=\frac{1}{3}(160 \hat{i}-5 \hat{j}-70 \hat{k})$

Hence, the required vector is $\frac{1}{3}(160 \hat{i}-5 \hat{j}-70 \hat{k})$.

13. The scalar product of the vector $\hat{i}+\hat{j}+\hat{k}$ with a unit vector along the sum of vectors $2 \hat{i}+4 \hat{j}-5 \hat{k}$ and $\lambda \hat{i}+2 \hat{j}+3 \hat{k}$ is equal to one. Find the value of $\lambda$.

Show Answer

Solution

$(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$

$=(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}$

Therefore, unit vector along $(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$ is given as:

$\frac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{(2+\lambda)^{2}+6^{2}+(-2)^{2}}}=\frac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{4+4 \lambda+\lambda^{2}+36+4}}=\frac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}$

Scalar product of $(\hat{i}+\hat{j}+\hat{k})$ with this unit vector is 1 .

$\Rightarrow(\hat{i}+\hat{j}+\hat{k}) \cdot \frac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \frac{(2+\lambda)+6-2}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \sqrt{\lambda^{2}+4 \lambda+44}=\lambda+6$

$\Rightarrow \lambda^{2}+4 \lambda+44=(\lambda+6)^{2}$

$\Rightarrow \lambda^{2}+4 \lambda+44=\lambda^{2}+12 \lambda+36$

$\Rightarrow 8 \lambda=8$

$\Rightarrow \lambda=1$

Hence, the value of $\lambda$ is 1 .

14. If $\vec{a}, \vec{b}, \overrightarrow{{}c}$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec{c} \cdot \vec{d}=15$ is equally inclined to $\vec{a}, \vec{b}$ and $\vec{c}$.

Show Answer

Solution

Since $\vec{a}, \vec{b}$, and $\vec{c}$ are mutually perpendicular vectors, we have

$\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$.

It is given that:

$|\vec{a}|=|\vec{b}|=|\vec{c}|$

Let vector $\vec{a}+\vec{b}+\vec{c}$ be inclined to $\vec{a}, \vec{b}$, and $\vec{c}$ at angles $\theta_1, \theta_2$, and $\theta_3$ respectively.

Then, we have:

$ \begin{aligned} \cos \theta_1 & =\frac{(\vec{a}+\vec{b}+\vec{c}) \cdot \vec{a}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|}=\frac{\vec{a} \cdot \vec{a}+\vec{b} \cdot \vec{a}+\vec{c} \cdot \vec{a}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|} \\ & =\frac{|\vec{a}|^{2}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|} \quad[\vec{b} \cdot \vec{a}=\vec{c} \cdot \vec{a}=0] \\ & =\frac{|\vec{a}|}{|\vec{a}+\vec{b}+\vec{c}|} \\ \cos \theta_2 & =\frac{(\vec{a}+\vec{b}+\vec{c}) \cdot \vec{b}}{|\vec{a}+\vec{b}+\vec{c}||\vec{b}|}=\frac{\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{b}+\vec{c} \cdot \vec{b}}{|\vec{a}+\vec{b}+\vec{c}| \cdot|\vec{b}|} \\ & =\frac{|\vec{b}|^{2}}{|\vec{a}+\vec{b}+\vec{c}| \cdot|\vec{b}|} \quad[\vec{a} \cdot \vec{b}=\vec{c} \cdot \vec{b}=0] \\ \cos \theta_3 & =\frac{\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{c}}{|\vec{a}+\vec{b}+\vec{c}||\vec{c}|} \\ & =\frac{|\vec{c}|^{2}}{|\vec{a}+\vec{b}+\vec{c}||\vec{c}|} \\ & =\frac{|\vec{c}|}{|\vec{a}+\vec{b}+\vec{c}|} \end{aligned} $

Now, as $|\vec{a}|=|\vec{b}|=|\vec{c}|, \cos \theta_1=\cos \theta_2=\cos \theta_3$.

$\therefore \theta_1=\theta_2=\theta_3$

Hence, the vector $(\vec{a}+\vec{b}+\vec{c})$ is equally inclined to $\vec{a}, \vec{b}$, and $\vec{c}$.

15. Prove that $(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}$, if and only if $\vec{a}, \vec{b}$ are perpendicular, given $\vec{a} \neq \overrightarrow{{}0}, \vec{b} \neq \overrightarrow{{}0}$.

Show Answer

Solution

$(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}$

$\Leftrightarrow \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b}=|\vec{a}|^{2}+|\vec{b}|^{2} \quad$ [Distributivity of scalar products over addition]

$\Leftrightarrow|\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2} \quad[\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}$ (Scalar product is commutative)

$\Leftrightarrow 2 \vec{a} \cdot \vec{b}=0$

$\Leftrightarrow \vec{a} \cdot \vec{b}=0$

$\therefore \vec{a}$ and $\vec{b}$ are perpendicular. $\quad[\vec{a} \neq \overrightarrow{{}0}, \vec{b} \neq \overrightarrow{{}0}$ (Given) $]$

Choose the correct answer in Exercises 16 to 19.

16. If $\theta$ is the angle between two vectors $\vec{a}$ and $\vec{b}$, then $\vec{a} \cdot \vec{b} \geq 0$ only when

(A) $0<\theta<\frac{\pi}{2}$

(B) $0 \leq \theta \leq \frac{\pi}{2}$

(C) $0<\theta<\pi$

(D) $0 \leq \theta \leq \pi$

Show Answer

Solution

Let $\theta$ be the angle between two vectors $\vec{a}$ and $\vec{b}$.

Then, without loss of generality, $\vec{a}$ and $\vec{b}$ are non-zero vectors so

that $|\vec{a}|$ and $|\vec{b}|$ are positive.

It is known that $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$.

$\therefore \vec{a} \cdot \vec{b} \geq 0$

$\Rightarrow|\vec{a}||\vec{b}| \cos \theta \geq 0$

$\Rightarrow \cos \theta \geq 0 \quad[|\vec{a}|$ and $|\vec{b}|$ are positive $]$

$\Rightarrow 0 \leq \theta \leq \frac{\pi}{2}$

Hence, $\vec{a} \cdot \vec{b} \geq 0$ when $0 \leq \theta \leq \frac{\pi}{2}$.

The correct answer is $B$.

17. Let $\vec{a}$ and $\vec{b}$ be two unit vectors and $\theta$ is the angle between them. Then $\vec{a}+\vec{b}$ is a unit vector if

(A) $\theta=\frac{\pi}{4}$

(B) $\theta=\frac{\pi}{3}$

(C) $\theta=\frac{\pi}{2}$

(D) $\theta=\frac{2 \pi}{3}$

Show Answer

Solution

Let $\vec{a}$ and $\vec{b}$ be two unit vectors and $\theta$ be the angle between them.

Then, $|\vec{a}|=|\vec{b}|=1$.

Now, $\vec{a}+\vec{b}$ is a unit vector if $|\vec{a}+\vec{b}|=1$.

$ \begin{aligned} & |\vec{a}+\vec{b}|=1 \\ & \Rightarrow(\vec{a}+\vec{b})^{2}=1 \\ & \Rightarrow(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=1 \\ & \Rightarrow \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b}=1 \\ & \Rightarrow|\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2}=1 \\ & \Rightarrow 1^{2}+2|\vec{a}||\vec{b}| \cos \theta+1^{2}=1 \\ & \Rightarrow 1+2 \cdot 1 \cdot 1 \cos \theta+1=1 \\ & \Rightarrow \cos \theta=-\frac{1}{2} \\ & \Rightarrow \theta=\frac{2 \pi}{3} \end{aligned} $

Hence, $\vec{a}+\vec{b}$ is a unit vector if $\theta=\frac{2 \pi}{3}$.

The correct answer is D.

18. The value of $\hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})+\hat{k} \cdot(\hat{i} \times \hat{j})$ is

(A) 0

(B) -1

(C) 1

(D) 3

Show Answer

Solution

$ \begin{aligned} & \hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})+\hat{k} \cdot(\hat{i} \times \hat{j}) \\ & =\hat{i} \cdot \hat{i}+\hat{j} \cdot(-\hat{j})+\hat{k} \cdot \hat{k} \\ & =1-\hat{j} \cdot \hat{j}+1 \\ & =1-1+1 \\ & =1 \end{aligned} $

The correct answer is C.

19. If $\theta$ is the angle between any two vectors $\vec{a}$ and $\vec{b}$, then $|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|$ when $\theta$ is equal to

(A) 0

(B) $\frac{\pi}{4}$

(C) $\frac{\pi}{2}$

(D) $\pi$

Show Answer

Solution

Let $\theta$ be the angle between two vectors $\vec{a}$ and $\vec{b}$.

Then, without loss of generality, $\vec{a}$ and $\vec{b}$ are non-zero vectors, so

that $|\vec{a}|$ and $|\vec{b}|$ are positive

$|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|$

$\Rightarrow|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta$

$\Rightarrow \cos \theta=\sin \theta \quad[|\vec{a}|$ and $|\vec{b}|$ are positive $]$

$\Rightarrow \tan \theta=1$

$\Rightarrow \theta=\frac{\pi}{4}$

Hence, $|\vec{a} \vec{b}|=|\vec{a} \times \vec{b}|$ when $\theta$ isequal to $\frac{\pi}{4}$.

The correct answer is $B$.

Summary

• Position vector of a point $P(x, y, z)$ is given as $\overrightarrow{{}OP}(=\vec{r})=x \hat{i}+y \hat{j}+z \hat{k}$, and its magnitude by $\sqrt{x^{2}+y^{2}+z^{2}}$.

• The scalar components of a vector are its direction ratios, and represent its projections along the respective axes.

• The magnitude $(r)$, direction ratios $(a, b, c)$ and direction cosines $(l, m, n)$ of any vector are related as:

$$ l=\frac{a}{r}, \quad m=\frac{b}{r}, \quad n=\frac{c}{r} $$

• The vector sum of the three sides of a triangle taken in order is $\overrightarrow{{}0}$.

• The vector sum of two coinitial vectors is given by the diagonal of the parallelogram whose adjacent sides are the given vectors.

• The multiplication of a given vector by a scalar $\lambda$, changes the magnitude of the vector by the multiple $|\lambda|$, and keeps the direction same (or makes it opposite) according as the value of $\lambda$ is positive (or negative).

• For a given vector $\vec{a}$, the vector $\hat{a}=\frac{\vec{a}}{|\vec{a}|}$ gives the unit vector in the direction of $\vec{a}$.

• The position vector of a point $R$ dividing a line segment joining the points $P$ and $Q$ whose position vectors are $\vec{a}$ and $\vec{b}$ respectively, in the ratio $m: n$ (i) internally, is given by $\frac{n \vec{a}+m \vec{b}}{m+n}$. (ii) externally, is given by $\frac{m \vec{b}-n \vec{a}}{m-n}$.

• The scalar product of two given vectors $\vec{a}$ and $\vec{b}$ having angle $\theta$ between them is defined as $$ \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta $$

• Also, when $\vec{a} \cdot \vec{b}$ is given, the angle ’ $\theta$ ’ between the vectors $\vec{a}$ and $\vec{b}$ may be determined by $$ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} $$ $\Delta$ If $\theta$ is the angle between two vectors $\vec{a}$ and $\vec{b}$, then their cross product is given as $$ \vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n} $$

• where $\hat{n}$ is a unit vector perpendicular to the plane containing $\vec{a}$ and $\vec{b}$. Such that $\vec{a}, \vec{b}, \hat{n}$ form right handed system of coordinate axes.

• If we have two vectors $\vec{a}$ and $\vec{b}$, given in component form as $\vec{a}=a _ {1} \hat{i}+a _ {2} \hat{j}+a _ {3} \hat{k}$ and $\vec{b}=b _ {1} \hat{i}+b _ {2} \hat{j}+b _ {3} \hat{k}$ and $\lambda$ any scalar, then $$ \begin{aligned} \vec{a}+\vec{b} & =(a _ {1}+b _ {1}) \hat{i}+(a _ {2}+b _ {2}) \hat{j}+(a _ {3}+b _ {3}) \hat{k} \\ \lambda \vec{a} & =(\lambda a _ {1}) \hat{i}+(\lambda a _ {2}) \hat{j}+(\lambda a _ {3}) \hat{k} \\ \vec{a} \cdot \vec{b} & =a _ {1} b _ {1}+a _ {2} b _ {2}+a _ {3} b _ {3} \end{aligned} $$ $$ \text{ and } \quad \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{vmatrix} \text{. } $$

Historical Note

The word vector has been derived from a Latin word vectus, which means “to carry”. The germinal ideas of modern vector theory date from around 1800 when Caspar Wessel (1745-1818) and Jean Robert Argand (1768-1822) described that how a complex number $a+i b$ could be given a geometric interpretation with the help of a directed line segment in a coordinate plane. William Rowen Hamilton (1805-1865) an Irish mathematician was the first to use the term vector for a directed line segment in his book Lectures on Quaternions (1853). Hamilton’s method of quaternions (an ordered set of four real numbers given as: $a+b \hat{i}+c \hat{j}+d \hat{k}, \hat{i}, \hat{j}, \hat{k}$ following certain algebraic rules) was a solution to the problem of multiplying vectors in three dimensional space. Though, we must mention here that in practice, the idea of vector concept and their addition was known much earlier ever since the time of Aristotle (384-322 B.C.), a Greek philosopher, and pupil of Plato (427-348 B.C.). That time it was supposed to be known that the combined action of two or more forces could be seen by adding them according to parallelogram law. The correct law for the composition of forces, that forces add vectorially, had been discovered in the case of perpendicular forces by Stevin-Simon (1548-1620). In 1586 A.D., he analysed the principle of geometric addition of forces in his treatise DeBeghinselen der Weeghconst (“Principles of the Art of Weighing”), which caused a major breakthrough in the development of mechanics. But it took another 200 years for the general concept of vectors to form.

In the 1880, Josaih Willard Gibbs (1839-1903), an American physicist and mathematician, and Oliver Heaviside (1850-1925), an English engineer, created what we now know as vector analysis, essentially by separating the real (scalar) part of quaternion from its imaginary (vector) part. In 1881 and 1884, Gibbs printed a treatise entitled Element of Vector Analysis. This book gave a systematic and concise account of vectors. However, much of the credit for demonstrating the applications of vectors is due to the D. Heaviside and P.G. Tait (1831-1901) who contributed significantly to this subject.