In most sciences one generation tears down what another has built and what one has established another undoes. In Mathematics alone each generation builds a new story to the old structure. - HERMAN HANKEL

10.1 भूमिका (Introduction)

अपने दैनिक जीवन में हमें अनेक प्रश्न मिलते हैं जैसे कि आपकी ऊँचाई क्या है? एक फुटबाल के खिलाड़ी को अपनी ही टीम के दूसरे खिलाड़ी के पास गेंद पहुँचाने के लिए गेंद पर किस प्रकार प्रहार करना चाहिए? अवलोकन कीजिए कि प्रथम प्रश्न का संभावित उत्तर 1.6 मीटर हो सकता है। यह एक ऐसी राशि है जिसमें केवल एक मान परिमाण जो एक वास्तविक संख्या है, सम्मिलित है। ऐसी राशियाँ अदिश कहलाती है। तथापि दूसरे प्रश्न का उत्तर एक ऐसी राशि है (जिसे बल कहते हैं) जिसमें मांसपेशियों की शक्ति परिमाण के साथ-साथ दिशा (जिसमें दूसरा खिलाड़ी स्थित है) भी सम्मिलित है। ऐसी राशियाँ सदिश कहलाती है। गणित, भौतिकी एवं अभियांत्रिकी में ये दोनों प्रकार की राशियाँ नामतः अदिश राशियाँ, जैसे कि लंबाई, द्रव्यमान, समय, दूरी, गति, क्षेत्रफल, आयतन, तापमान, कार्य, धन,वोल्टता, घनत्व, प्रतिरोधक इत्यादि एवं सदिश राशियाँ जैसे कि विस्थापन, वेग, त्वरण, बल, भार, संवेग, विद्युत क्षेत्र की तीव्रता इत्यादि बहुधा मिलती हैं।

W.R. Hamilton (1805-1865)

इस अध्याय में हम सदिशों की कुछ आधारभूत संकल्पनाएँ, सदिशों की विभिन्न संक्रियाएँ और इनके बीजीय एवं ज्यामितीय गुणधर्मों का अध्ययन करेंगे। इन दोनों प्रकार के गुणधर्मों का सम्मिलित रूप सदिशों की संकल्पना का पूर्ण अनुभूति देता है और उपर्युक्त चर्चित क्षेत्रों में इनकी विशाल उपयोगिता की ओर प्रेरित करता है।

10.2 कुछ आधारभूत संकल्पनाएँ (Some Basic Concepts)

मान लीजिए कि किसी तल अथवा त्रि-विमीय अंतरिक्ष में $l$ कोई सरल रेखा है। तीर के निशानों की सहायता से इस रेखा को दो दिशाएँ प्रदान की जा सकती हैं। इन दोनों में से निश्चित दिशा वाली कोई भी एक रेखा दिष्ट रेखा कहलाती है [आकृति 10.1 (i), (ii)]।

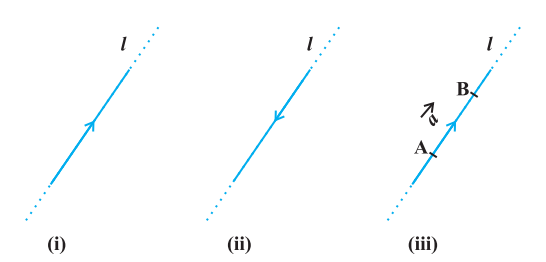
आकृति 10.1

अब प्रेक्षित कीजिए कि यदि हम रेखा ’ $l$ ’ को रेखाखंड $\mathrm{AB}$ तक प्रतिबंधित कर देते हैं तब दोनों मे से किसी एक दिशा वाली रेखा ’ $l$ ’ पर परिमाण निर्धारित हो जाता है। इस प्रकार हमें एक दिष्ट रेखाखंड प्राप्त होता है (आकृति 10.1(iii))।अतः एक दिष्ट रेखाखंड में परिमाण एवं दिशा दोनों होते हैं।

परिभाषा 1 एक ऐसी राशि जिसमें परिमाण एवं दिशा दोनों होते हैं, सदिश कहलाती है।

ध्यान दीजिए कि एक दिष्ट रेखाखंड सदिश होता है (आकृति 10.1(iii)), जिसे $\overrightarrow{\mathrm{AB}}$ अथवा साधारणतः $\vec{a}$, के रूप में निर्दिष्ट करते हैं और इसे सदिश ’ $\overrightarrow{\mathrm{AB}}$ ’ अथवा सदिश ’ $\vec{a}$ ’ के रूप में पढ़ते हैं।

वह बिंदु $\mathrm{A}$ जहाँ से सदिश $\overrightarrow{\mathrm{AB}}$ प्रारंभ होता है, प्रारंभिक बिंदु कहलाता है और वह बिंदु $\mathrm{B}$ जहाँ पर सदिश $\overrightarrow{\mathrm{AB}}$, समाप्त होता है अंतिम बिंदु कहलाता है। किसी सदिश के प्रारंभिक एवं अंतिम बिंदुओं के बीच की दूरी सदिश का परिमाण (अथवा लंबाई) कहलाता है और इसे $|\overrightarrow{\mathrm{AB}}|$ अथवा $|\vec{a}|$ के रूप में निर्दिष्ट किया जाता है। तीर का निशान सदिश की दिशा को निर्दिष्ट करता है।

टिप्पणी क्योंकि लंबाई कभी भी ऋणात्मक नहीं होती है इसलिए संकेतन $|\vec{a}|<0$ का कोई अर्थ नहीं है।

स्थिति सदिश (Position Vector)

कक्षा XI से, त्रि-विमीय दक्षिणावर्ती समकोणिक निर्देशांक पद्धति को स्मरण कीजिए ( आकृति $10.2(\mathrm{i})) ।$ अंतरिक्ष में मूल बिंदु $\mathrm{O}(0,0,0)$ के सापेक्ष एक ऐसा बिंदु $\mathrm{P}$ लीजिए जिसके निर्देशांक $(x, y, z)$ है। तब सदिश $\overrightarrow{\mathrm{OP}}$ जिसमें $\mathrm{O}$ और $\mathrm{P}$ क्रमशः प्रारंभिक एवं अंतिम बिंदु हैं, $\mathrm{O}$ के सापेक्ष बिंदु $\mathrm{P}$ का स्थिति सदिश कहलाता है। दूरी सूत्र (कक्षा $\mathrm{XI}$ से) का उपयोग करते हुए $\overrightarrow{\mathrm{OP}}$ (अथवा $\vec{r}$ ) का परिमाण निम्नलिखित रूप में प्राप्त होता है:

$$ |\overrightarrow{{}OP}|=\sqrt{x^{2}+y^{2}+z^{2}} $$

व्यवहार में मूल बिंदु $\mathrm{O}$ के सापेक्ष, बिंदुओं $\mathrm{A}, \mathrm{B}, \mathrm{C}$ इत्यादि के स्थिति सदिश क्रमशः $\vec{a}, \vec{b}, \vec{c}$ से निर्दिष्ट किए जाते हैं [आकृति 10.2(ii)]।

आकृति 10.2

दिक्-कोसाइन (Direction Cosines)

एक बिंदु $\mathrm{P}(x, y, z)$ का स्थिति सदिश $\overrightarrow{\mathrm{OP}}($ अथवा $\vec{r}$ ) लीजिए जैसा कि आकृति 10.3 में दर्शाया गया है। सदिश $\vec{r}$ द्वारा $x, y$ एवं $z$-अक्ष की धनात्मक दिशाओं के साथ बनाए गए क्रमशः कोण $\alpha, \beta$, एवं $\gamma$ दिशा कोण कहलाते हैं। इन कोणों के कोसाइन मान अर्थात् $\cos \alpha, \cos \beta$ एवं $\cos \gamma$ सदिश $\vec{r}$ के दिक्-कोसाइन कहलाते हैं और सामान्यतः इनको क्रमशः $l, m$ एवं $n$ से निर्दिष्ट किया जाता है।

आकृति 10.3 , से हम देखते हैं कि त्रिभुज OAP एक समकोण त्रिभुज है और इस त्रिभुज से हम $\cos \alpha=\frac{x}{r}(r$ को $|\vec{r}|$ के लिए प्रयोग किया गया है) प्राप्त करते हैं। इसी प्रकार समकोण त्रिभुजों $\mathrm{OBP}$ एवं $\mathrm{OCP}$ से हम $\cos \beta=\frac{y}{r}$ एवं $\cos \gamma=\frac{z}{r}$ लिख सकते हैं। इस प्रकार बिंदु $\mathrm{P}$ के निर्देशांकों को $(l r, m r, n r)$ के रूप में अभिव्यक्त किया जा सकता है। दिक्-कोसाइन के समानुपाती संख्याएँ $l r$, $m r$ एवं $n r$ सदिश $\vec{r}$ के दिक्-अनुपात कहलाते हैं और इनको क्रमश: $a, b$ तथा $c$ से निर्दिष्ट किया जाता है।

टिप्पणी हम नोट कर सकते हैं कि $l^{2}+m^{2}+n^{2}=1$ परंतु सामान्यत: $a^{2}+b^{2}+c^{2} \neq 1$

10.3 सदिशों के प्रकार (Types of Vectors)

शून्य सदिश [Zero (null) Vector] एक सदिश जिसके प्रारंभिक एवं अंतिम बिंदु संपाती होते हैं, शून्य सदिश कहलाता है और इसे $\overrightarrow{\mathbf{0}}$ के रूप में निर्दिष्ट किया जाता है। शून्य सदिश को कोई निश्चित दिशा प्रदान नहीं की जा सकती क्योंकि इसका परिमाण शून्य होता है अथवा विकल्पतः इसको कोई भी दिशा धारण किए हुए माना जा सकता है। सदिश $\overrightarrow{\mathrm{AA}}, \overrightarrow{\mathrm{BB}}$ शून्य सदिश को निरूपित करते हैं।

मात्रक सदिश (Unit Vector) एक सदिश जिसका परिमाण एक (अथवा 1 इकाई) है मात्रक सदिश कहलाता है। किसी दिए हुए सदिश $\vec{a}$ की दिशा में मात्रक सदिश को $\hat{a}$ से निर्दिष्ट किया जाता है। सह-आदिम सदिश (Co-initial Vectors) दो अथवा अधिक सदिश जिनका एक ही प्रारंभिक बिंदु है, सह आदिम सदिश कहलाते हैं।

संरेख सदिश (Collinear Vectors) दो अथवा अधिक सदिश यदि एक ही रेखा के समांतर है तो वे संरेख सदिश कहलाते हैं।

समान सदिश (Equal Vectors) दो सदिश $\vec{a}$ तथा $\vec{b}$ समान सदिश कहलाते हैं यदि उनके परिमाण एवं दिशा समान हैं। इनको $\vec{a}=\vec{b}$ के रूप में लिखा जाता है।

ॠणात्मक सदिश (Negative of a Vector) एक सदिश जिसका परिमाण दिए हुए सदिश (मान लीजिए $\overrightarrow{\mathrm{AB}}$ ) के समान है परंतु जिसकी दिशा दिए हुए सदिश की दिशा के विपरीत है, दिए हुए सदिश का ॠणात्मक कहलाता है। उदाहरणतः सदिश $\overrightarrow{\mathrm{BA}}$, सदिश $\overrightarrow{\mathrm{AB}}$ का ऋणात्मक है और इसे $\overrightarrow{\mathrm{BA}}=-\overrightarrow{\mathrm{AB}}$ के रूप में लिखा जाता है।

टिप्पणी उपर्युक्त परिभाषित सदिश इस प्रकार है कि उनमें से किसी को भी उसके परिमाण एवं दिशा को परिवर्तित किए बिना स्वयं के समांतर विस्थापित किया जा सकता है। इस प्रकार के सदिश स्वतंत्र सदिश कहलाते हैं। इस पूरे अध्याय में हम स्वतंत्र सदिशों की ही चर्चा करेंगे।

उदाहरण 1 दक्षिण से $30^{\circ}$ पश्चिम में, $40 \mathrm{~km}$ के विस्थापन का आलेखीय निरूपण कीजिए।

हल सदिश $\overrightarrow{\mathrm{OP}}$ अभीष्ट विस्थापन को निरूपित करता है (आकृति 10.4 देखिए)।

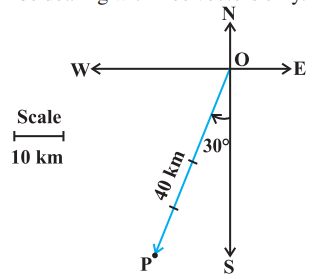
आकृति 10.4

उदाहरण 2 निम्नलिखित मापों को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।

(i) $5 \mathrm{~s}$

(ii) $1000 \mathrm{~cm}^{3}$

(iii) $10 \mathrm{~N}$

(iv) $30 \mathrm{~km} / \mathrm{h}$

(v) $10 \mathrm{~g} / \mathrm{cm}^{3}$

(vi) $20 \mathrm{~m} / \mathrm{s}$ उत्तर की ओर

हल

(i) समय-अदिश

(ii) आयतन-अदिश

(iii) बल-सदिश

(iv) गति-अदिश

(v) घनत्व-अदिश

(vi) वेग-सदिश

उदाहरण 3 आकृति 10.5 में कौन से सदिश

(i) संरेख हैं

(ii) समान हैं

(iii) सह-आदिम हैं

हल

(i) संरेख सदिश : $\vec{a}, \vec{c}$ तथा $\vec{d}$

(ii) समान सदिश : $\vec{a}$ तथा $\vec{c}$

(iii) सह-आदिम सदिश : $\vec{b}, \vec{c}$ तथा $\vec{d}$

प्रश्नावली 10.1

1. उत्तर से $30^{\circ}$ पूर्व में $40 \mathrm{~km}$ के विस्थापन का आलेखीय निरूपण कीजिए।

Show Answer

#missing

2. निम्नलिखित मापों को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।

(i) $10 \mathrm{~kg}$

(ii) 2 मीटर उत्तर-पश्चिम

(iii) $40^{\circ}$

(iv) 40 वाट

(v) $10^{-19}$ कूलंब

(vi) $20 \mathrm{~m} / \mathrm{s}^2$

Show Answer

#missing

3. निम्नलिखित को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।

(i) समय कालांश

(ii) दूरी

(iii) बल

(iv) वेग

(v) कार्य

Show Answer

#missing

4. आकृति 10.6 (एक वर्ग) में निम्नलिखित सदिशों को पहचानिए।

(i) सह-आदिम

(ii) समान

(iii) संरेख परंतु असमान

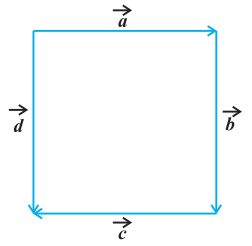
Show Answer

#missing

5. निम्नलिखित का उत्तर सत्य अथवा असत्य के रूप में दीजिए।

(i) $\vec{a}$ तथा $-\vec{a}$ संरेख हैं।

(ii) दो संरेख सदिशों का परिमाण सदैव समान होता है।

(iii) समान परिमाण वाले दो सदिश संरेख होते हैं।

आकृति 10.6

(iv) समान परिमाण वाले दो संरेख सदिश समान होते हैं।

Show Answer

#missing

10.4 सदिशों का योगफल (Addition of Vectors)

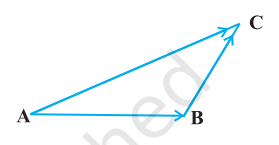
सदिश $\overrightarrow{\mathrm{AB}}$ से साधारणतः हमारा तात्पर्य है बिंदु $\mathrm{A}$ से बिंदु $\mathrm{B}$ तक विस्थापन। अब एक ऐसी स्थिति की चर्चा कीजिए जिसमें एक लड़की बिंदु $A$ से बिंदु $B$ तक चलती है और उसके बाद बिंदु $\mathrm{B}$ से बिंदु $\mathrm{C}$ तक चलती है (आकृति 10.7)। बिंदु $\mathrm{A}$ से बिंदु $C$ तक लड़की द्वारा किया गया कुल विस्थापन सदिश, $\overrightarrow{\mathrm{AC}}$ से प्राप्त होता है और इसे

आकृति 10.7

$\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}$ के रूप में अभिव्यक्त किया जाता है।

यह सदिश योग का त्रिभुज नियम कहलाता है।

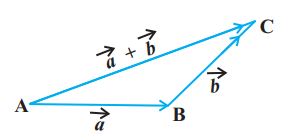
सामान्यतः, यदि हमारे पास दो सदिश $\vec{a}$ तथा $\vec{b}$ हैं [आकृति 10.8 (i)], तो उनका योग ज्ञात करने के लिए उन्हें इस स्थिति में लाया जाता है, ताकि एक का प्रारंभिक बिंदु दूसरे के अंतिम बिंदु के संपाती हो जाए [आकृति 10.8(ii)]।

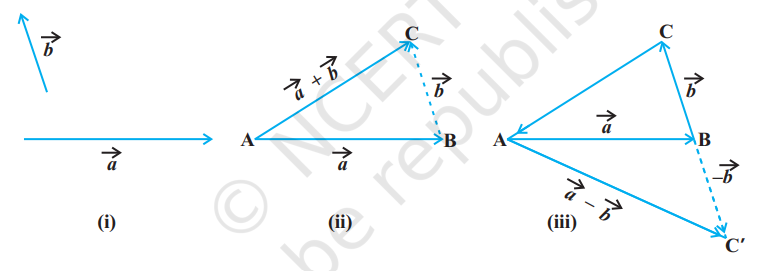
आकृति 10.8

उदाहरणतः आकृति 10.8 (ii) में, हमने सदिश $\vec{b}$ के परिमाण एवं दिशा को परिवर्तित किए बिना इस प्रकार स्थानांतरित किया है ताकि इसका प्रारंभिक बिंदु, $\vec{a}$ के अंतिम बिंदु के संपाती है तब त्रिभुज $\mathrm{ABC}$ की तीसरी भुजा $\mathrm{AC}$ द्वारा निरूपित सदिश $\vec{a}+\vec{b}$ हमें सदिशों $\vec{a}$ तथा $\vec{b}$ का योग (अथवा परिणामी) प्रदान करता है, अर्थात् त्रिभुज $\mathrm{ABC}$ में हम पाते हैं कि

$\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}$

अब पुनः क्योंकि $\overrightarrow{\mathrm{AC}}=-\overrightarrow{\mathrm{CA}}$, इसलिए उपर्युक्त समीकरण से हम पाते हैं कि

$$ \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{\mathrm{AA}}=\overrightarrow{0} $$

इसका तात्पर्य यह है कि किसी त्रिभुज की भुजाओं को यदि एक क्रम में लिया जाए तो यह शून्य परिणामी की ओर प्रेरित करता है क्योंकि प्रारंभिक एवं अंतिम बिंदु संपाती हो जाते हैं [आकृति 10.8(iii)]।

अब एक सदिश $\overrightarrow{\mathrm{BC}^{\prime}}$ की रचना इस प्रकार कीजिए ताकि इसका परिमाण सदिश $\overrightarrow{\mathrm{BC}}$, के परिमाण के समान हो, परंतु इसकी दिशा $\overrightarrow{\mathrm{BC}}$ की दिशा के विपरीत हो आकृति 10.8(iii) अर्थात् $\overrightarrow{\mathrm{BC}}^{\prime}=-\overrightarrow{\mathrm{BC}}$ तब त्रिभुज नियम का अनुप्रयोग करते हुए [आकृति 10.8(iii)] से हम पाते हैं कि $\overrightarrow{\mathrm{AC}^{\prime}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}^{\prime}}=\overrightarrow{\mathrm{AB}}+(-\overrightarrow{\mathrm{BC}})=\vec{a}-\vec{b}$

सदिश $\overrightarrow{\mathrm{AC}^{\prime}}, \vec{a}$ तथा $\vec{b}$ के अंतर को निरूपित करता है।

अब किसी नदी के एक किनारे से दूसरे किनारे तक पानी के बहाव की दिशा के लंबवत् जाने वाली एक नाव की चर्चा करते हैं। तब इस नाव पर दो वेग सदिश कार्य कर रहे हैं, एक इंजन द्वारा नाव को दिया गया वेग और दूसरा नदी के पानी के बहाव का वेग। इन दो वेगों के युगपत प्रभाव से नाव वास्तव में एक भिन्न वेग से चलना शुरू करती है। इस नाव की प्रभावी गति एवं दिशा (अर्थात् परिणामी वेग) के बारे में यथार्थ विचार लाने के लिए हमारे पास सदिश योगफल का निम्नलिखित नियम है।

यदि हमारे पास एक समांतर चतुर्भुज की दो संलग्न भुजाओं से निरूपित किए जाने वाले (परिमाण एवं दिशा सहित) दो सदिश $\vec{a}$ तथा $\vec{b}$ है (आकृति 10.9) तब समांतर चतुर्भुज की इन दोनों भुजाओं के उभयनिष्ठ बिंदु से गुजरने वाला विकर्ण इन दोनों सदिशों के योग $\vec{a}+\vec{b}$ को परिमाण एवं दिशा सहित निरूपित करता है। यह सदिश योग का समांतर चतुर्भुज नियम कहलाता है।

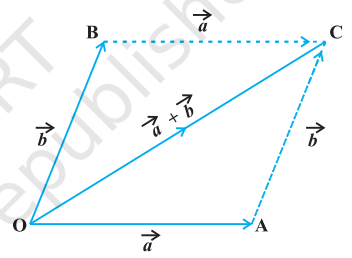
आकृति 10.9

टिप्पणी त्रिभुज नियम का उपयोग करते हुए आकृति 10.9 से हम नोट कर सकते हैं कि

$\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OC}}$ या $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}$ (क्योंकि $\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OB}}$ )

जो कि समांतर चतुर्भुज नियम है। अतः हम कह सकते हैं कि सदिश योग के दो नियम एक दूसरे के समतुल्य हैं।

सदिश योगफल के गुणधर्म (Properties of vector addition)

गुणधर्म 1 दो सदिशों $\vec{a}$ तथा $\vec{b}$ के लिए

$ \vec{a}+\vec{b}=\vec{b}+\vec{a} \tag{क्रमविनिमयता} $

उपपत्ति समांतर चतुर्भुज $\mathrm{ABCD}$ को लीजिए (आकृति 10.10) मान लीजिए $\overrightarrow{\mathrm{AB}}=\vec{a}$ और $\overrightarrow{\mathrm{BC}}=\vec{b}$, तब त्रिभुज $\mathrm{ABC}$ में त्रिभुज नियम का उपयोग करते हुए हम पाते हैं कि $\overrightarrow{\mathrm{AC}}=\vec{a}+\vec{b}$

अब, क्योंकि समांतर चतुर्भुज की सम्मुख भुजाएँ समान एवं समांतर है, इसलिए आकृति 10.10 में $\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{BC}}=\vec{b}$ और $\overrightarrow{\mathrm{DC}}=\overrightarrow{\mathrm{AB}}=\vec{a}$ है।

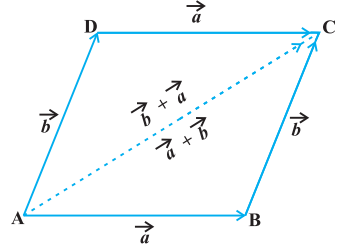
आकृति 10.10 पुनः त्रिभुज $\mathrm{ADC}$ में त्रिभुज नियम के प्रयोग से

$\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DC}}$ $=\vec{b}+\vec{a}$

अत:

$\vec{a}+\vec{b}=\vec{b}+\vec{a}$

गुणधर्म 2 तीन सदिशों $\vec{a}, \vec{b}$ और $\vec{c}$ के लिए

$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) \quad$ (साहचर्य गुण)

उपपत्ति मान लीजिए, सदिशों $\vec{a}, \vec{b}$ तथा $\vec{c}$ को क्रमशः $\overrightarrow{\mathrm{PQ}}, \overrightarrow{\mathrm{QR}}$ एवं $\overrightarrow{\mathrm{RS}}$ से निरूपित किया गया है जैसा कि आकृति 10.11(i) और (ii) में दर्शाया गया है।

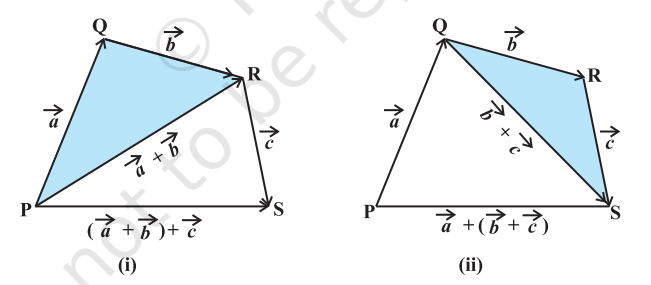
आकृति 10.11

तब $$ \vec{a}+\vec{b}=\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{QR}}=\overrightarrow{\mathrm{PR}} $$

और $$ \vec{b}+\vec{c}=\overrightarrow{\mathrm{QR}}+\overrightarrow{\mathrm{RS}}=\overrightarrow{\mathrm{QS}} $$

इसलिए $$ (\vec{a}+\vec{b})+\vec{c}=\overrightarrow{\mathrm{PR}}+\overrightarrow{\mathrm{RS}}=\overrightarrow{\mathrm{PS}} $$

और $$ \vec{a}+(\vec{b}+\vec{c})=\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{QS}}=\overrightarrow{\mathrm{PS}} $$

इस तरह $$ (\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) $$

टिप्पणी सदिश योगफल के साहचर्य गुणधर्म की सहायता से हम तीन सदिशों $\vec{a}, \vec{b}$ तथा $\vec{c}$ का योगफल कोष्ठकों का उपयोग किए बिना $\vec{a}+\vec{b}+\vec{c}$ के रूप में लिखते हैं।

नोट कीजिए कि किसी सदिश $\vec{a}$ के लिए हम पाते हैं:

$$ \vec{a}+\overrightarrow{0}=\overrightarrow{0}+\vec{a}=\vec{a} $$

यहाँ शून्य सदिश $\overrightarrow{0}$ सदिश योगफल के लिए योज्य सर्वसमिका कहलाता है।

10.5 एक अदिश से सदिश का गुणन (Multiplication of a Vector by a Scalar)

मान लीजिए कि $\vec{a}$ एक दिया हुआ सदिश है और $\lambda$ एक अदिश है। तब सदिश $\vec{a}$ का अदिश $\lambda$, से गुणनफल जिसे $\lambda \vec{a}$ के रूप में निर्दिष्ट किया जाता है, सदिश $\vec{a}$ का अदिश $\lambda$ से गुणन कहलाता है। नोट कीजिए कि $\lambda \vec{a}$ भी सदिश $\vec{a}$ के संरेख एक सदिश है। $\lambda$ के मान धनात्मक अथवा ऋणात्मक होने के अनुसार $\lambda \vec{a}$ की दिशा, $\vec{a}$ के समान अथवा विपरीत होती है। $\lambda \vec{a}$ का परिमाण $\vec{a}$ के परिमाण का $|\lambda|$ गुणा होता है, अर्थात्

$$ |\lambda \vec{a}|=|\lambda||\vec{a}| $$

एक अदिश से सदिश के गुणन का ज्यामितीय चाक्षुषीकरण [रूप की कल्पना (visualisation)] आकृति 10.12 में दी गई है।

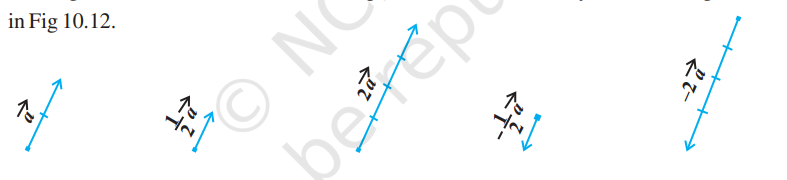
आकृति 10.12

जब $\lambda=-1$, तब $\lambda \vec{a}=-\vec{a}$ जो एक ऐसा सदिश है जिसका परिमाण $\vec{a}$ के समान है और दिशा $\vec{a}$ की दिशा के विपरीत है। सदिश $-\vec{a}$ सदिश $\vec{a}$ का ऋणात्मक (अथवा योज्य प्रतिलोम)कहलाता है और हम हमेशा

$\vec{a}+(-\vec{a})=(-\vec{a})+\vec{a}=\overrightarrow{0}$ पाते हैं।

और यदि $\lambda=\frac{1}{|\vec{a}|}$, दिया हुआ है कि $\vec{a} \neq 0$, अर्थात् $\vec{a}$ एक शून्य सदिश नहीं है

तब $$ |\lambda \vec{a}|=|\lambda||\vec{a}|=\frac{1}{|\vec{a}|}|\vec{a}|=1 $$

इस प्रकार $\lambda \vec{a}, \vec{a}$ की दिशा में मात्रक सदिश को निरूपित करता है। हम इसे

$$ \hat{a}=\frac{1}{|\vec{a}|} \vec{a} \text { के रूप में लिखते हैं। } $$

टिप्पणी किसी भी अदिश $k$ के लिए $k \overrightarrow{0}=\overrightarrow{0}$

10.5.1 एक सदिश के घटक (Components of a vector)

आईए बिंदुओं $\mathrm{A}(1,0,0), \mathrm{B}(0,1,0)$ और $\mathrm{C}(0,0,1)$ को क्रमशः $x$-अक्ष, $y$-अक्ष एवं $z$-अक्ष पर लेते हैं। तब स्पष्टतः

$$ |\overrightarrow{\mathrm{OA}}|=1,|\overrightarrow{\mathrm{OB}}|=1 \text { और }|\overrightarrow{\mathrm{OC}}|=1 $$

सदिश $\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}$ और $\overrightarrow{\mathrm{OC}}$ जिनमें से प्रत्येक का परिमाण 1 हैं $\mathbf{X}^{K}$ क्रमशः $\mathrm{OX}, \mathrm{OY}$ और $\mathrm{OZ}$ अक्षों के अनुदिश मात्रक सदिश कहलाते हैं आकृति 10.13 और इनको क्रमशः $\hat{i}, \hat{j}$ और $\hat{k}$ द्वारा निर्दिष्ट किया जाता है (आकृति 10.13)।

अब एक बिंदु $\mathrm{P}(x, y, z)$ का स्थिति सदिश $\overrightarrow{\mathrm{OP}}$ लीजिए जैसा कि आकृति 10.14 में दर्शाया गया है। मान लीजिए कि बिंदु $\mathrm{P} _{1}$ से तल $\mathrm{XOY}$ पर खींचे गए लंब का पाद बिंदु $\mathrm{P} _{1}$ है। इस प्रकार हम देखते हैं कि $\mathrm{P} _{1} \mathrm{P}, z$-अक्ष के समांतर है। क्योंकि $\hat{i}, \hat{j}$ एवं $\hat{k}$ क्रमशः $x, y$ एवं $z$-अक्ष के अनुदिश मात्रक सदिश है और $\mathrm{P}$ के निर्देशांकों की परिभाषा के अनुसार हम पाते हैं कि $\overrightarrow{\mathrm{P} _{1} \mathrm{P}}=\overrightarrow{\mathrm{OR}}=z \hat{k}$. इसी प्रकार $\overrightarrow{\mathrm{QP} _{1}}=\overrightarrow{\mathrm{OS}}=y \hat{j}$ और $\overrightarrow{\mathrm{OQ}}=x \hat{i}$. इस प्रकार हम पाते हैं कि

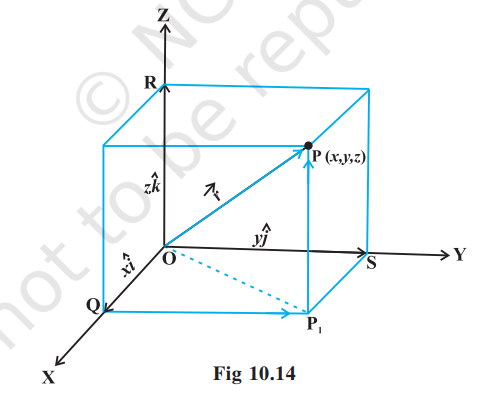
और

$$ \begin{aligned} & \overrightarrow{\mathrm{OP} _{1}}=\overrightarrow{\mathrm{OQ}}+\overrightarrow{\mathrm{QP} _{1}}=x \hat{i}+y \hat{j} \\ & \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OP} _{1}}+\overrightarrow{\mathrm{P} _{1} \mathrm{P}}=x \hat{i}+y \hat{j}+z \hat{k} \end{aligned} $$

इस प्रकार $\mathrm{O}$ के सापेक्ष $\mathrm{P}$ का स्थिति सदिश

$\overrightarrow{\mathrm{OP}}$ (अथवा $\vec{r}$ ) $=x \hat{i}+y \hat{j}+z \hat{k}$ के रूप में प्राप्त होता है।

किसी भी सदिश का यह रूप घटक रूप कहलाता है। यहाँ $x, y$ एवं $z, \vec{r}$ के अदिश घटक कहलाते हैं और $x \hat{i}, y \hat{j}$ एवं $z \hat{k}$ क्रमागत अक्षों के अनुदिश $\vec{r}$ के सदिश घटक कहलाते हैं। कभी-कभी $x, y$ एवं $z$ को समकोणिक घटक भी कहा जाता है।

किसी सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$, की लंबाई पाइथागोरस प्रमेय का दो बार प्रयोग करके तुरंत ज्ञात की जा सकती है। हम नोट करते हैं कि समकोण त्रिभुज $\mathrm{OQP} _{1}$ में (आकृति 10.14)

$$ \left|\overrightarrow{\mathrm{OP} _{1}}\right|=\sqrt{|\overrightarrow{\mathrm{OQ}}|^{2}+\left|\overrightarrow{\mathrm{QP} _{1}}\right|^{2}}=\sqrt{x^{2}+y^{2}} $$

और समकोण त्रिभुज $\mathrm{OP} _{1} \mathrm{P}$, में हम पाते हैं कि

$$ |\overrightarrow{\mathrm{OP}}|=\sqrt{\left|\overrightarrow{\mathrm{OP} _{1}}\right|^{2}+\left|\overrightarrow{\mathrm{P} _{1} \mathrm{P}}\right|^{2}}=\sqrt{\left(x^{2}+y^{2}\right)+z^{2}} $$

अतः किसी सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ की लंबाई $|\vec{r}|=|x \hat{i}+y \hat{j}+z \hat{k}|=\sqrt{x^{2}+y^{2}+z^{2}}$ के रूप में प्राप्त होती है।

यदि दो सदिश $\vec{a}$ और $\vec{b}$ घटक रूप में क्रमशः $a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ और $b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}$ द्वारा दिए गए हैं तो

(i) सदिशों $\vec{a}$ और $\vec{b}$ को योग

$$ \vec{a}+\vec{b}=\left(a _{1}+b _{1}\right) \hat{i}+\left(a _{2}+b _{2}\right) \hat{j}+\left(a _{3}+b _{3}\right) \hat{k} \text { के रूप में प्राप्त होता है। } $$

(ii) सदिश $\vec{a}$ और $\vec{b}$ का अंतर

$$ \vec{a}-\vec{b}=\left(a _{1}-b _{1}\right) \hat{i}+\left(a _{2}-b _{2}\right) \hat{j}+\left(a _{3}-b _{3}\right) \hat{k} \text { के रूप में प्राप्त होता है। } $$

(iii) सदिश $\vec{a}$ और $\vec{b}$ समान होते हैं यदि और केवल यदि

$$ a _{1}=b _{1}, a _{2}=b _{2} \text { और } a _{3}=b _{3} $$

(iv) किसी अदिश $\lambda$ से सदिश $\vec{a}$ का गुणन

$$ \lambda \vec{a}=\left(\lambda a _{1}\right) \hat{i}+\left(\lambda a _{2}\right) \hat{j}+\left(\lambda a _{3}\right) \hat{k} \text { द्वारा प्रदत्त है। } $$

सदिशों का योगफल और किसी अदिश से सदिश का गुणन सम्मिलित रूप में निम्नलिखित वितरण-नियम से मिलता है

मान लीजिए कि $\vec{a}$ और $\vec{b}$ कोई दो सदिश हैं और $k$ एवं $m$ दो अदिश हैं तब

(i) $k \vec{a}+m \vec{a}=(k+m) \vec{a}$

(ii) $k(m \vec{a})=(k m) \vec{a}$

(iii) $k(\vec{a}+\vec{b})=k \vec{a}+k \vec{b}$

टिप्पणी

1. आप प्रेक्षित कर सकते हैं कि $\lambda$ के किसी भी मान के लिए सदिश $\lambda \vec{a}$ हमेशा सदिश $\vec{a}$ के संरेख है। वास्तव में दो सदिश $\vec{a}$ और $\vec{b}$ संरेख तभी होते हैं यदि और केवल यदि एक ऐसे शून्येतर अदिश $\lambda$ का अस्तित्व हैं ताकि $\vec{b}=\lambda \vec{a}$ हो। यदि सदिश $\vec{a}$ और $\vec{b}$ घटक रूप में दिए हुए हैं, अर्थात् $\vec{a}=a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ और $\vec{b}=b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}$, तब दो सदिश संरेख होते हैं यदि और केवल यदि

$$ \begin{array}{cc} & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda\left(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\right) \\ \Leftrightarrow & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\left(\lambda a_1\right) \hat{i}+\left(\lambda a_2\right) \hat{j}+\left(\lambda a_3\right) \hat{k} \\ \Leftrightarrow & b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3 \\ \Leftrightarrow & \frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}=\lambda \end{array} $$

2. यदि $\vec{a}=a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ तब $a _{1}, a _{2}, a _{3}$ सदिश $\vec{a}$ के दिक्-अनुपात कहलाते हैं।

3. यदि $l, m, n$ किसी सदिश के दिक्-कोसाइन हैं तब $$ l \hat{i}+m \hat{j}+n \hat{k}=(\cos \alpha) \hat{i}+(\cos \beta) \hat{j}+(\cos \gamma) \hat{k} $$ दिए हुए सदिश की दिशा में मात्रक सदिश है जहाँ $\alpha, \beta$ एवं $\gamma$ दिए हुए सदिश द्वारा क्रमशः $x$, $y$ एवं $z$ अक्ष के साथ बनाए गए कोण हैं।

उदाहरण $4 x, y$ और $z$ के मान ज्ञात कीजिए ताकि सदिश $\vec{a}=x \hat{i}+2 \hat{j}+z \hat{k}$ और $\vec{b}=2 \hat{i}+y \hat{j}+\hat{k}$ समान हैं।

हल ध्यान दीजिए कि दो सदिश समान होते हैं यदि और केवल यदि उनके संगत घटक समान है। अतः दिए हुए सदिश $\vec{a}$ और $\vec{b}$ समान होंगे यदि और केवल यदि $x=2, y=2, z=1$

उदाहरण 5 मान लीजिए $\vec{a}=\hat{i}+2 \hat{j}$ और $\vec{b}=2 \hat{i}+\hat{j}$ तब क्या $|\vec{a}|=|\vec{b}|$ है ? क्या सदिश $\vec{a}$ और $\vec{b}$ समान हैं ?

हल यहाँ $|\vec{a}|=\sqrt{1^{2}+2^{2}}=\sqrt{5}$ और $|\vec{b}|=\sqrt{2^{2}+1^{2}}=\sqrt{5}$

इसलिए $|\vec{a}|=|\vec{b}|$ परंतु दिए हुए सदिश समान नहीं हैं क्योंकि इनके संगत घटक भिन्न हैं।

उदाहरण 6 सदिश $\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}$ के अनुदिश मात्रक सदिश ज्ञात कीजिए।

हल सदिश $\vec{a}$ के अनुदिश मात्रक सदिश $\hat{a}=\frac{1}{|\vec{a}|} \vec{a}$ द्वारा प्राप्त होता है।

अब $ |\vec{a}|=\sqrt{2^{2}+3^{2}+1^{2}}=\sqrt{14} $

इसलिए $ \hat{a}=\frac{1}{\sqrt{14}}(2 \hat{i}+3 \hat{j}+\hat{k})=\frac{2}{\sqrt{14}} \hat{i}+\frac{3}{\sqrt{14}} \hat{j}+\frac{1}{\sqrt{14}} \hat{k} $

उदाहरण 7 सदिश $\vec{a}=\hat{i}-2 \hat{j}$ के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 7 इकाई है।

हल दिए हुए सदिश $\vec{a}$ के अनुदिश मात्रक सदिश $\hat{a}=\frac{1}{|\vec{a}|} \vec{a}=\frac{1}{\sqrt{5}}(\hat{i}-2 \hat{j})=\frac{1}{\sqrt{5}} \hat{i}-\frac{2}{\sqrt{5}} \hat{j}$ है। इसलिए $\vec{a}$ के अनुदिश और 7 परिमाण वाला सदिश $7 \hat{a}=7\left(\frac{1}{\sqrt{5}} \hat{i}-\frac{2}{\sqrt{5}} \hat{j}\right)=\frac{7}{\sqrt{5}} \hat{i}-\frac{14}{\sqrt{5}} \hat{j}$ है।

उदाहरण 8 सदिशों $\vec{a}=2 \hat{i}+2 \hat{j}-5 \hat{k}$ और $\vec{b}=2 \hat{i}+\hat{j}+3 \hat{k}$ के योगफल के अनुदिश मात्रक सदिश ज्ञात कीजिए।

हल दिए हुए सदिशों का योगफल

$ \begin{aligned} & \vec{a}+\vec{b}(=\vec{c}, \text{ say })=4 \hat{i}+3 \hat{j}-2 \hat{k} \\ \text {और } \qquad & \quad|\vec{c}|=\sqrt{4^{2}+3^{2}+(-2)^{2}}=\sqrt{29} \end{aligned} $

अतः अभीष्ट मात्रक सदिश

$$ \hat{c}=\frac{1}{|\vec{c}|} \vec{c}=\frac{1}{\sqrt{29}}(4 \hat{i}+3 \hat{j}-2 \hat{k})=\frac{4}{\sqrt{29}} \hat{i}+\frac{3}{\sqrt{29}} \hat{j}-\frac{2}{\sqrt{29}} \hat{k} \text { है। } $$

उदाहरण 9 सदिश $\vec{a}=\hat{i}+\hat{j}-2 \hat{k}$ के दिक्-अनुपात लिखिए और इसकी सहायता से दिक्-कोसाइन ज्ञात कीजिए।

हल ध्यान दीजिए कि सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ के दिक्-अनुपात $a, b, c$ सदिश के, क्रमागत घटक $x, y, z$ होते हैं। इसलिए दिए हुए सदिश के लिए हम पाते हैं कि $a=1, b=1$ और $c=-2$ है। पुन: यदि $l, m$ और $n$ दिए हुए सदिश के दिक्-कोसाइन हैं तो:

$$ l=\frac{a}{|\vec{r}|}=\frac{1}{\sqrt{6}}, \quad m=\frac{b}{|\vec{r}|}=\frac{1}{\sqrt{6}}, \quad n=\frac{c}{|\vec{r}|}=\frac{-2}{\sqrt{6}}(\text { क्योंकि }|\vec{r}|=\sqrt{6}) $$

अतः दिक्-कोसाइन $\left(\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}}\right)$ हैं।

10.5.2 दो बिंदुओं को मिलाने वाला सदिश (Vector joining two points)

यदि $\mathrm{P} _{1}\left(x _{1}, y _{1}, z _{1}\right)$ और $\mathrm{P} _{2}\left(x _{2}, y _{2}, z _{2}\right)$ दो बिंदु हैं तब $\mathrm{P} _{1}$ को $\mathrm{P} _{2}$ से मिलाने वाला सदिश $\overrightarrow{\mathrm{P} _{1}}$ है (आकृति 10.15)। $\mathrm{P} _{1}$ और $\mathrm{P} _{2}$ को मूल बिंदु $\mathrm{O}$ से मिलाने पर और त्रिभुज नियम का प्रयोग करने पर हम त्रिभुज $\mathrm{OP} _{1} \mathrm{P} _{2}$ से पाते हैं कि $\overrightarrow{\mathrm{OP} _{1}}+\overrightarrow{\mathrm{P} _{1} \mathrm{P} _{2}}=\overrightarrow{\mathrm{OP} _{2}}$

सदिश योगफल के गुणधर्मों का उपयोग करते हुए उपर्युक्त समीकरण निम्नलिखित रूप से लिखा जाता है।

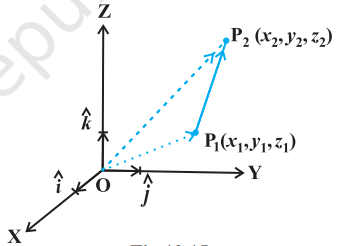
आकृति 10.15

$$ \text{ i.e. } \quad \begin{aligned} \overrightarrow{{}P_1 P_2} & =\overrightarrow{{}OP_2}-\overrightarrow{{}OP_1} \\ \overrightarrow{{}P_1 P_2} & =(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k})-(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}) \\ & =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} \end{aligned} $$

सदिश $\overrightarrow{\mathrm{P} _{1} \mathrm{P} _{2}}$ का परिमाण $\left|\overrightarrow{\mathrm{P} _{1} \mathrm{P} _{2}}\right|=\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}+\left(z _{2}-z _{1}\right)^{2}}$ के रूप में प्राप्त होता है।

उदाहरण 10 बिंदुओं $\mathrm{P}(2,3,0)$ एवं $\mathrm{Q}(-1,-2,-4)$ को मिलाने वाला एवं $\mathrm{P}$ से $\mathrm{Q}$ की तरफ दिष्ट सदिश ज्ञात कीजिए।

हल क्योंकि सदिश $\mathrm{P}$ से $\mathrm{Q}$ की तरफ दिष्ट है, स्पष्टतः $\mathrm{P}$ प्रारंभिक बिंदु है और $\mathrm{Q}$ अंतिम बिंदु है, इसलिए $\mathrm{P}$ और $\mathrm{Q}$ को मिलाने वाला अभीष्ट सदिश $\overrightarrow{\mathrm{PQ}}$, निम्नलिखित रूप में प्राप्त होता है।

$$ \begin{aligned} & \overrightarrow{{}PQ}=(-1-2) \hat{i}+(-2-3) \hat{j}+(-4-0) \hat{k} \\ \text { अर्थात } \qquad & \overrightarrow{{}PQ}=-3 \hat{i}-5 \hat{j}-4 \hat{k} \end{aligned} $$

10.5.3 खंड सूत्र (Section Formula)

मान लीजिए मूल बिंदु $\mathrm{O}$ के सापेक्ष $\mathrm{P}$ और $\mathrm{Q}$ दो बिंदु हैं जिनको स्थिति सदिश $\overrightarrow{\mathrm{OP}}$ और $\overrightarrow{\mathrm{OQ}}$ से निरूपित किया गया है। बिंदुओं $P$ एवं $Q$ को मिलाने वाला रेखा खंड किसी तीसरे बिंदु $\mathrm{R}$ द्वारा दो प्रकार से विभाजित किया जा सकता है। अंत: (आकृति 10.16) एवं बाह्य (आकृति 10.17)। यहाँ हमारा उद्देश्य मूल बिंदु $\mathrm{O}$ के सापेक्ष बिंदु $\mathrm{R}$ का स्थिति सदिश $\overrightarrow{\mathrm{OR}}$ ज्ञात करना है। हम दोनों स्थितियों को एक-एक करके लेते हैं।

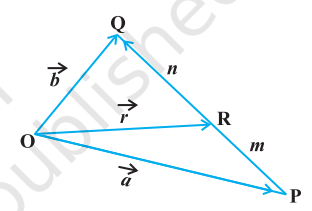
आकृति 10.16

स्थिति 1 जब R, PQ को अंतः विभाजित करता है ( आकृति 10.16)। यदि $\mathrm{R}, \overrightarrow{\mathrm{PQ}}$ को इस प्रकार विभाजित करता है कि $m \overrightarrow{\mathrm{RQ}}=n \overrightarrow{\mathrm{PR}}$, जहाँ $m$ और $n$ धनात्मक अदिश हैं तो हम कहते हैं

कि बिंदु $\mathrm{R}, \overrightarrow{\mathrm{PQ}}$ को $m: n$ के अनुपात में अंतः विभाजित करता है। अब त्रिभुजों $\mathrm{ORQ}$ एवं $\mathrm{OPR}$ से

$$ \overrightarrow{\mathrm{RQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OR}}=\vec{b}-\vec{r} $$

$$ \text { और } \qquad \overrightarrow{{}PR}=\overrightarrow{{}OR}-\overrightarrow{{}OP}=\vec{r}-\vec{a} $$

$$ \begin{aligned} \text { इसलिए } \qquad m(\vec{b}-\vec{r}) & =n(\vec{r}-\vec{a}) \quad \text{ (क्यों?) } \end{aligned} $$

$$ \begin{aligned} \text {अथवा } \qquad \vec{r} & =\frac{m \vec{b}+n \vec{a}}{m+n} \qquad \text{ (सरलकरनेपर) } \end{aligned} $$

अतः बिंदु $\mathrm{R}$ जो कि $\mathrm{P}$ और $\mathrm{Q}$ को $m: n$ के अनुपात में अंतः विभाजित करता है का स्थिति सदिश

$$ \overrightarrow{\mathrm{OR}}=\frac{m \vec{b}+n \vec{a}}{m+n} \text { के रूप में प्राप्त होता है। } $$

स्थिति II जब R, PQ को बाह्य विभाजित करता है ( आकृति 10.17)। यह सत्यापन करना हम पाठक के लिए एक प्रश्न के रूप में छोड़ते हैं कि रेखाखंड $\mathrm{PQ}$ को $m: n$ के अनुपात में बाह्य विभाजित करने वाले बिंदु $\mathrm{R}\left(\right.$ i.e., $\left.\frac{\mathrm{PR}}{\mathrm{QR}}=\frac{m}{n}\right)$ का स्थिति सदिश $\overrightarrow{\mathrm{OR}}=\frac{m \vec{b}-n \vec{a}}{m-n}$ के रूप में प्राप्त होता है।

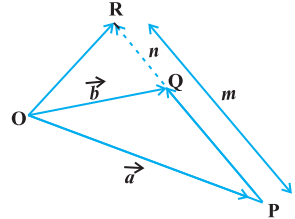
आकृति 10.17

टिप्पणी यदि $\mathrm{R}, \mathrm{PQ}$ का मध्य बिंदु है तो $m=n$ और इसलिए स्थिति $\mathrm{I}$ से $\overrightarrow{\mathrm{PQ}}$ के मध्य बिंदु $\mathrm{R}$ का स्थिति सदिश $\overrightarrow{\mathrm{OR}}=\frac{\vec{a}+\vec{b}}{2}$ के रूप में होगा।

उदाहरण 11 दो बिंदु $\mathrm{P}$ और $\mathrm{Q}$ लीजिए जिनके स्थिति सदिश $\overrightarrow{\mathrm{OP}}=3 \vec{a}-2 \vec{b}$ और $\overrightarrow{\mathrm{OQ}}=\vec{a}+\vec{b}$ हैं। एक ऐसे बिंदु $R$ का स्थिति सदिश ज्ञात कीजिए जो $P$ एवं $Q$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में (i) अंतः (ii) बाह्य विभाजित करता है।

हल

(i) $\mathrm{P}$ और $\mathrm{Q}$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में अंतः विभाजित करने वाले बिंदु $\mathrm{R}$ का स्थिति सदिश है:

$$ \overrightarrow{\mathrm{OR}}=\frac{2(\vec{a}+\vec{b})+(3 \vec{a}-2 \vec{b})}{3}=\frac{5 \vec{a}}{3} $$

(ii) $\mathrm{P}$ और $\mathrm{Q}$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में बाह्य विभाजित करने वाले बिंदु $\mathrm{R}$ का स्थिति सदिश है:

$$ \overrightarrow{\mathrm{OR}}=\frac{2(\vec{a}+\vec{b})-(3 \vec{a}-2 \vec{b})}{2-1}=4 \vec{b}-\vec{a} $$

उदाहरण 12 दर्शाइए कि बिंदु $\mathrm{A}(2 \hat{i}-\hat{j}+\hat{k}), \mathrm{B}(\hat{i}-3 \hat{j}-5 \hat{k}), \mathrm{C}(3 \hat{i}-4 j-4 \hat{k})$ एक समकोण त्रिभुज के शीर्ष हैं।

हल हम पाते हैं कि

$$ \begin{aligned} & \overrightarrow{\mathrm{AB}}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k} \\ & \overrightarrow{\mathrm{BC}}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k} \end{aligned} $$

$$ \overrightarrow{\mathrm{CA}}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k} $$

इसके अतिरिक्त ध्यान दीजिए कि

$$ |\overrightarrow{\mathrm{AB}}|^{2}=41=6+35=|\overrightarrow{\mathrm{BC}}|^{2}+|\overrightarrow{\mathrm{CA}}|^{2} $$

अतः दिया हुआ त्रिभुज एक समकोण त्रिभुज है।

प्रश्नावली 10.2

1. निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए:

$$ \vec{a}=\hat{i}+\hat{j}+\hat{k} ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k} $$

Show Answer

#missing

2. समान परिमाण वाले दो विभिन्न सदिश लिखिए।

Show Answer

#missing

3. समान दिशा वाले दो विभिन्न सदिश लिखिए।

Show Answer

#missing

4. $x$ और $y$ के मान ज्ञात कीजिए ताकि सदिश $2 \hat{i}+3 \hat{j}$ और $x \hat{i}+y \hat{j}$ समान हों।

Show Answer

#missing

5. एक सदिश का प्रारंभिक बिंदु $(2,1)$ है और अंतिम बिंदु $(-5,7)$ है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए।

Show Answer

#missing

6. सदिश $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ और $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$ का योगफल ज्ञात कीजिए।

Show Answer

#missing

7. सदिश $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$ के अनुदिश एक मात्रक सदिश ज्ञात कीजिए।

Show Answer

#missing

8. सदिश $\overrightarrow{\mathrm{PQ}}$, के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ बिंदु $\mathrm{P}$ और $\mathrm{Q}$ क्रमशः $(1,2,3)$ और $(4,5,6)$ हैं।

Show Answer

#missing

9. दिए हुए सदिशों $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ और $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$, के लिए, सदिश $\vec{a}+\vec{b}$ के अनुदिश मात्रक सदिश ज्ञात कीजिए।

Show Answer

#missing

10. सदिश $5 \hat{i}-\hat{j}+2 \hat{k}$ के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 8 इकाई है।

Show Answer

#missing

11. दर्शाइए कि सदिश $2 \hat{i}-3 \hat{j}+4 \hat{k}$ और $-4 \hat{i}+6 \hat{j}-8 \hat{k}$ संरेख हैं।

Show Answer

#missing

12. सदिश $\hat{i}+2 \hat{j}+3 \hat{k}$ की दिक् cosine ज्ञात कीजिए।

Show Answer

#missing

13. बिंदुओं $\mathrm{A}(1,2,-3)$ एवं $\mathrm{B}(-1,-2,1)$ को मिलाने वाले एवं $\mathrm{A}$ से $\mathrm{B}$ की तरफ़ दिष्ट सदिश की दिक् cosine ज्ञात कीजिए।

Show Answer

#missing

14. दर्शाइए कि सदिश $\hat{i}+\hat{j}+\hat{k}$ अक्षों $\mathrm{OX}, \mathrm{OY}$ एवं $\mathrm{OZ}$ के साथ बराबर झुका हुआ है।

Show Answer

#missing

15. बिंदुओं $\mathrm{P}(\hat{i}+2 \hat{j}-\hat{k})$ और $\mathrm{Q}(-\hat{i}+\hat{j}+\hat{k})$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में

(i) अंतः

(ii) बाह्य, विभाजित करने वाले बिंदु $R$ का स्थिति सदिश ज्ञात कीजिए।

Show Answer

#missing

16. दो बिंदुओं $\mathrm{P}(2,3,4)$ और $\mathrm{Q}(4,1,-2)$ को मिलाने वाले सदिश का मध्य बिंदु ज्ञात कीजिए।

Show Answer

#missing

17. दर्शाइए कि बिंदु $\mathrm{A}, \mathrm{B}$ और $\mathrm{C}$, जिनके स्थिति सदिश क्रमश: $\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ और $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$ हैं, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।

Show Answer

#missing

18. त्रिभुज $\mathrm{ABC}$ (आकृति 10.18), के लिए निम्नलिखित में से कौन सा कथन सत्य नहीं है।

(A) $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$

(B) $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{AC}}=\overrightarrow{0}$

(C) $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$

(D) $\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$

आकृति 10.18

Show Answer

#missing

19. यदि $\vec{a}$ और $\vec{b}$ दो संरेख सदिश हैं तो निम्नलिखित में से कौन सा कथन सही नहीं है:

(A) $\vec{b}=\lambda \vec{a}$, किसी अदिश $\lambda$ के लिए

(B) $\vec{a}= \pm \vec{b}$

(C) $\vec{a}$ और $\vec{b}$ के क्रमागत घटक समानुपाती नहीं हैं।

(D) दोनों सदिशों $\vec{a}$ तथा $\vec{b}$ की दिशा समान है परंतु परिमाण विभिन्न हैं।

Show Answer

#missing

10.6 दो सदिशों का गुणनफल (Product of Two Vectors)

अभी तक हमने सदिशों के योगफल एवं व्यवकलन के बारे में अध्ययन किया है। अब हमारा उद्देश्य सदिशों का गुणनफल नामक एक दूसरी बीजीय संक्रिया की चर्चा करना है। हम स्मरण कर सकते हैं कि दो संख्याओं का गुणनफल एक संख्या होती है, दो आव्यूहों का गुणनफल एक आव्यूह होता है परंतु फलनों की स्थिति में हम उन्हें दो प्रकार से गुणा कर सकते हैं नामतः दो फलनों का बिंदुवार गुणन एवं दो फलनों का संयोजन। इसी प्रकार सदिशों का गुणन भी दो तरीके से परिभाषित किया जाता है। नामतः अदिश गुणनफल जहाँ परिणाम एक अदिश होता है और सदिश गुणनफल जहाँ परिणाम एक सदिश होता है। सदिशों के इन दो प्रकार के गुणनफलों के आधार पर ज्यामिती, यांत्रिकी एवं अभियांत्रिकी में इनके विभिन्न अनुप्रयोग हैं। इस परिच्छेद में हम इन दो प्रकार के गुणनफलों की चर्चा करेंगे।

10.6.1 दो सदिशों का अदिश गुणनफल [Scalar (or dot) product of two vectors]

परिभाषा 2 दो शून्येतर सदिशों $\vec{a}$ और $\vec{b}$ का अदिश गुणनफल $\vec{a} \cdot \vec{b}$ द्वारा निर्दिष्ट किया जाता है और इसे $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$ के रूप मे परिभाषित किया जाता है। जहाँ $\theta, \vec{a}$ और $\vec{b}$, के बीच का कोण है और $0 \leq \theta \leq \pi$ (आकृति 10.19)। यदि $\vec{a}=\overrightarrow{0}$ अथवा $\vec{b}=\overrightarrow{0}$, तो $\theta$ परिभाषित नहीं है और इस स्थिति में हम $\vec{a} \cdot \vec{b}=0$ परिभाषित करते हैं।

आकृति 10.19

प्रेक्षण

1. $\vec{a} \cdot \vec{b}$ एक वास्तविक संख्या है।

2. मान लीजिए कि $\vec{a}$ और $\vec{b}$ दो शून्येतर सदिश हैं तब $\vec{a} \cdot \vec{b}=0$ यदि और केवल यदि $\vec{a}$ और $\vec{b}$ परस्पर लंबवत् हैं अर्थात् $$\vec{a} \cdot \vec{b}=0 \Leftrightarrow \vec{a} \perp \vec{b}$$

3. यदि $\theta=0$, तब $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$

विशिष्टतः $\vec{a} \cdot \vec{a}=|\vec{a}|^{2}$, क्योंकि इस स्थिति में $\theta=0$ है।

4. यदि $\theta=\pi$, तब $\vec{a} \cdot \vec{b}=-|\vec{a}||\vec{b}|$

विशिष्टत: $\vec{a} \cdot(-\vec{a})=-|\vec{a}|^{2}$, जैसा कि इस स्थिति में $\theta, \pi$ के बराबर है।

5. प्रेक्षण 2 एवं 3 के संदर्भ में परस्पर लंबवत् मात्रक सदिशों $\hat{i}, \hat{j}$ एवं $\hat{k}$, के लिए हम पाते हैं कि

तथा $$ \begin{aligned} & \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1 \\ & \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 \end{aligned} $$

6. दो शून्येतर सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$,

$$ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} \text { अथवा } \theta=\cos ^{-1}\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right) \text { द्वारा दिया जाता है। } $$

7. अदिश गुणनफल क्रम विनिमेय है अर्थात्

$$ \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} \quad \text { (क्यों?) } $$

अदिश गुणनफल के दो महत्वपूर्ण गुणधर्म (Two important properties of scalar product)

गुणधर्म 1 (अदिश गुणनफल की योगफल पर वितरण नियम) मान लीजिए $\vec{a}, \vec{b}$ और $\vec{c}$ तीन सदिश हैं तब

$\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}$

गुणधर्म 2 मान लीजिए $\vec{a}$ और $\vec{b}$ दो सदिश हैं और $\lambda$ एक अदिश है, तो

$$ (\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b}) $$

यदि दो सदिश घटक रूप में $a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ एवं $b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}$, दिए हुए हैं तब उनका अदिश गुणनफल निम्नलिखित रूप में प्राप्त होता है

$ \begin{aligned} \vec{a} \cdot \vec{b}= & (a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}) \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 \hat{i} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_2 \hat{j} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_3 \hat{k} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ \text{ इस प्रकार } = & a_1 b_1(\hat{i} \cdot \hat{i})+a_1 b_2(\hat{i} \cdot \hat{j})+a_1 b_3(\hat{i} \cdot \hat{k})+a_2 b_1(\hat{j} \cdot \hat{i})+a_2 b_2(\hat{j} \cdot \hat{j})+a_2 b_3(\hat{j} \cdot \hat{k}) +a_3 b_1(\hat{k} \cdot \hat{i})+a_3 b_2(\hat{k} \cdot \hat{j})+a_3 b_3(\hat{k} \cdot \hat{k}) \qquad \text{ (उपर्युक्त गुणधर्म 1 और 2 का उपयोग करने पर ) } \\ = & a_1 b_1+a_2 b_2+a_3 b_3 \qquad \text{ (प्रक्षेण 5 का उपयोग करने पर) } \\ \qquad & \vec{a} \cdot \vec{b}=a_1 b_1+a_2 b_2+a_3 b_3 \end{aligned} $

10.6.2 एक सदिश का किसी रेखा पर साथ प्रक्षेप (Projection of a vector on a line)

मान लीजिए कि एक सदिश $\overrightarrow{\mathrm{AB}}$ किसी दिष्ट रेखा $l$ (मान लीजिए) के साथ वामावर्त दिशा में $\theta$ कोण बनाता है। (आकृति 10.20 देखिए) तब $\overrightarrow{\mathrm{AB}}$ का $l$ पर प्रक्षेप एक सदिश $\vec{p}$ (मान लीजिए) है जिसका परिमाण $|\overrightarrow{\mathrm{AB}}||\cos \theta|$ है और जिसकी दिशा का $l$ की दिशा के समान अथवा विपरीत होना इस बात पर निर्भर है कि $\cos \theta$ धनात्मक है अथवा ऋणात्मक। सदिश $\vec{p}$ को प्रक्षेप सदिश कहते हैं

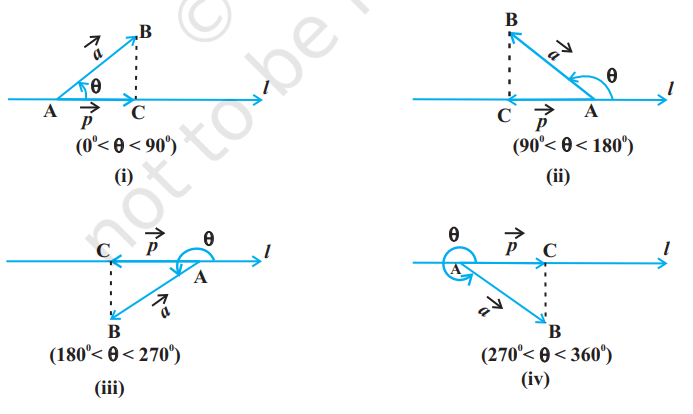
और इसका परिमाण $|\vec{p}|$, निर्दिष्ट रेखा $l$ पर सदिश $\overrightarrow{\mathrm{AB}}$ का प्रक्षेप कहलाता है। उदाहरणतः निम्नलिखित में से प्रत्येक आकृति में सदिश $\overrightarrow{\mathrm{AB}}$ का रेखा $l$ पर प्रक्षेप सदिश $\overrightarrow{\mathrm{AC}}$ है।

प्रेक्षण

1. रेखा $l$ के अनुदिश यदि $\hat{p}$ मात्रक सदिश है तो रेखा $l$ पर सदिश $\vec{a}$ का प्रक्षेप $\vec{a} . \hat{p}$ से प्राप्त होता है।

2. एक सदिश $\vec{a}$ का दूसरे सदिश $\vec{b}$, पर प्रक्षेप $\vec{a} \cdot \hat{b}$, अथवा $\vec{a} \cdot\left(\frac{\vec{b}}{|\vec{b}|}\right)$, अथवा $\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})$ से प्राप्त होता है।

3. यदि $\theta=0$, तो $\overrightarrow{\mathrm{AB}}$ का प्रक्षेप सदिश स्वयं $\overrightarrow{\mathrm{AB}}$ होगा और यदि $\theta=\pi$ तो $\overrightarrow{\mathrm{AB}}$ का प्रक्षेप सदिश $\overrightarrow{\mathrm{BA}}$ होगा।

4. यदि $\theta=\frac{\pi}{2}$ अथवा $\theta=\frac{3 \pi}{2}$ तो $\overrightarrow{\mathrm{AB}}$ का प्रक्षेप सदिश शून्य सदिश होगा।

टिप्पणी यदि $\alpha, \beta$ और $\gamma$ सदिश $\vec{a}=a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ के दिक्-कोण हैं तो इसकी दिक्-कोसाइन निम्नलिखित रूप में प्राप्त की जा सकती है।

$$ \cos \alpha=\frac{\vec{a} \cdot \hat{i}}{|\vec{a}||\hat{i}|}=\frac{a _{1}}{|\vec{a}|}, \cos \beta=\frac{a _{2}}{|\vec{a}|}, \text { and } \cos \gamma=\frac{a _{3}}{|\vec{a}|} $$

यह भी ध्यान दीजिए कि $|\vec{a}| \cos \alpha,|\vec{a}| \cos \beta$ और $|\vec{a}| \cos \gamma$ क्रमशः OX, OY तथा OZ के अनुदिश $\vec{a}$ के प्रक्षेप हैं अर्थात् सदिश $\vec{a}$ के अदिश घटक $a _{1}, a _{2}$ और $a _{3}$ क्रमश: $x, y$, एवं $z$ अक्ष के अनुदिश $\vec{a}$ के प्रक्षेप है। इसके अतिरिक्त यदि $\vec{a}$ एक मात्रक सदिश है तब इसको दिक्-कोसाइन की सहायता से के रूप में अभिव्यक्त किया जा सकता है।

$$ \vec{a}=\cos \alpha \hat{i}+\cos \beta \hat{j}+\cos \gamma \hat{k} $$

उदाहरण 13 दो सदिशों $\vec{a}$ और $\vec{b}$ के परिमाण क्रमशः 1 और 2 है तथा $\vec{a} \cdot \vec{b}=1$, इन सदिशों के बीच का कोण ज्ञात कीजिए।

हल दिया हुआ है $\vec{a} \cdot \vec{b}=1,|\vec{a}|=1$ और $|\vec{b}|=2$. अत:

$$ \theta=\cos ^{-1}\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right)=\cos ^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{3} $$

उदाहरण 14 सदिश $\vec{a}=\hat{i}+\hat{j}-\hat{k}$ तथा $\vec{b}=\hat{i}-\hat{j}+\hat{k}$ के बीच का कोण ज्ञात कीजिए।

हल दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ निम्न द्वारा प्रदत्त है

से प्राप्त होता है। $$ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} $$

अब $$ \begin{aligned} & \vec{a} \cdot \vec{b}=(\hat{i}+\hat{j}-\hat{k}) \cdot(\hat{i}-\hat{j}+\hat{k})=1-1-1=-1 \\ & \cos \theta=\frac{-1}{3} \end{aligned} $$

इसलिए, हम पाते हैं कि अतः अभीष्ट कोण $$ \theta=\cos ^{-1}\left(-\frac{1}{3}\right) \text { है। } $$

उदाहरण 15 यदि $\vec{a}=5 \hat{i}-\hat{j}-3 \hat{k}$ और $\vec{b}=\hat{i}+3 \hat{j}-5 \hat{k}$, तो दर्शाइए कि सदिश $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ लंबवत् है।

हल हम जानते हैं कि दो शून्येतर सदिश लंबवत् होते हैं यदि उनका अदिश गुणनफल शून्य है।

यहाँ $$ \vec{a}+\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})+(\hat{i}+3 \hat{j}-5 \hat{k})=6 \hat{i}+2 \hat{j}-8 \hat{k} $$

और $$ \vec{a}-\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})-(\hat{i}+3 \hat{j}-5 \hat{k})=4 \hat{i}-4 \hat{j}+2 \hat{k} $$

इसलिए $$ (\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=(6 \hat{i}+2 \hat{j}-8 \hat{k}) \cdot(4 \hat{i}-4 \hat{j}+2 \hat{k})=24-8-16=0 $$

अतः $\vec{a}+\vec{b} \text { और } \vec{a}-\vec{b} \text { लंबवत् सदिश हैं। }$

उदाहरण 16 सदिश $\vec{a}=2 \hat{i}+3 \hat{j}+2 \hat{k}$ का, सदिश $\vec{b}=\hat{i}+2 \hat{j}+\hat{k}$ पर प्रक्षेप ज्ञात कीजिए।

हल सदिश $\vec{a}$ का सदिश $\vec{b}$ पर प्रक्षेप

$$ \frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{1}{\sqrt{(1)^{2}+(2)^{2}+(1)^{2}}}(2.1+3.2+2.1)=\frac{10}{\sqrt{6}}=\frac{5}{3} \sqrt{6} \text { है। } $$

उदाहरण 17 यदि दो सदिश $\vec{a}$ और $\vec{b}$ इस प्रकार हैं कि $|\vec{a}|=2,|\vec{b}|=3$ और $\vec{a} \cdot \vec{b}=4$ तो $|\vec{a}-\vec{b}|$ ज्ञात कीजिए।

हल हम पाते हैं कि इसलिए

$$ \begin{aligned} |\vec{a}-\vec{b}|^{2} & =(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{b}) \\ & =\vec{a} \cdot \vec{a}-\vec{a} \cdot \vec{b}-\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \\ & =|\vec{a}|^{2}-2(\vec{a} \cdot \vec{b})+|\vec{b}|^{2} \\ & =(2)^{2}-2(4)+(3)^{2} \end{aligned} $$

उदाहरण 18 यदि $\vec{a}$ एक मात्रक सदिश है और $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8$, तो $|\vec{x}|$ ज्ञात कीजिए।

हल क्योंकि $\vec{a}$ एक मात्रक सदिश है, इसलिए $|\vec{a}|=1$. यह भी दिया हुआ है कि

$$ (\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8 $$

अथवा $ \vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\vec{a} \cdot \vec{a}=8 $

अथवा $ \vec{x}|^{2}-1=8 \text { अर्थात् }|\vec{x}|^{2}=9 $

इसलिए $|\vec{x}|=3$ (क्योंकि सदिश का परिमाण सदैव शून्येतर होता है)

उदाहरण 19 दो सदिशों $\vec{a}$ और $\vec{b}$, के लिए सदैव $|\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$ (Cauchy-Schwartz असमिका)।

हल दी हुई असमिका सहज रूप में स्पष्ट है यदि $\vec{a}=\overrightarrow{0}$ अथवा $\vec{b}=\overrightarrow{0}$. वास्तव में इस स्थिति में हम पाते हैं कि $|\vec{a} \cdot \vec{b}|=0=|\vec{a}||\vec{b}|$. इसलिए हम कल्पना करते हैं कि $|\vec{a}| \neq 0 \neq|\vec{b}|$ तब हमें

इसलिए $$ \frac{|\vec{a} \cdot \vec{b}|}{|\vec{a}||\vec{b}|}=|\cos \theta| \leq 1 \text { मिलता है। } $$

$\quad|\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$

आकृति 10.21

उदाहरण 20 दो सदिशों $\vec{a}$ तथा $\vec{b}$ के लिए सदैव $|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$ (त्रिभुज-असमिका)

हल दी हुई असमिका, दोनों स्थितियों $\vec{a}=0$ या $\vec{b}=0$ में सहज रूप से स्पष्ट है (क्यों ?)। इसलिए मान लीजिए कि $|\vec{a}| \neq \overrightarrow{0} \neq|\vec{b}|$ तब

$$ \begin{aligned} |\vec{a}+\vec{b}|^{2}= & (\vec{a}+\vec{b})^{2}=(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b}) \\ = & \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \\ = & |\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a} \cdot \vec{b}|+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a}||\vec{b}|+|\vec{b}|^{2} \\ = & (|\vec{a}|+|\vec{b}|)^{2} \\ & |\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}| \end{aligned} $$

टिप्पणी यदि समानता त्रिभुज असमानता में है (उपरोक्त उदाहरण 20 में), यानी।

तब $$ \begin{aligned} |\vec{a}+\vec{b}| & =|\vec{a}|+|\vec{b}| \\ |\overrightarrow{{}AC}| & =|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}| \end{aligned} $$

यह दर्शाता है कि बिंदु $A, B$ और $C$ संरेख हैं।

उदाहरण 21 दर्शाइए कि बिंदु $\mathrm{A}(-2 \hat{i}+3 \hat{j}+5 \hat{k}), \mathrm{B}(\hat{i}+2 \hat{j}+3 \hat{k})$ और $\mathrm{C}(7 \hat{i}-\hat{k})$ संरेख है।

हल हम प्राप्त करते हैं:

$$ \begin{aligned} \overrightarrow{{}AB} & =(1+2) \hat{i}+(2-3) \hat{j}+(3-5) \hat{k}=3 \hat{i}-\hat{j}-2 \hat{k} \\ \overrightarrow{{}BC} & =(7-1) \hat{i}+(0-2) \hat{j}+(-1-3) \hat{k}=6 \hat{i}-2 \hat{j}-4 \hat{k} \\ \overrightarrow{{}AC} & =(7+2) \hat{i}+(0-3) \hat{j}+(-1-5) \hat{k}=9 \hat{i}-3 \hat{j}-6 \hat{k} \\ |\overrightarrow{{}AB}| & =\sqrt{14},|\overrightarrow{{}BC}|=2 \sqrt{14} \text{ and }|\overrightarrow{{}AC}|=3 \sqrt{14} \end{aligned} $$

इसलिए $$ |\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}| $$

अतः बिंदु $\mathrm{A}, \mathrm{B}$ और $\mathrm{C}$ संरेख हैं।

टिप्पणी उदाहरण 21 में ध्यान दीजिए कि $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$ परंतु फिर भी बिंदु $\mathrm{A}$, $\mathrm{B}$ और $\mathrm{C}$ त्रिभुज के शीर्षों का निर्माण नहीं करते हैं।

प्रश्नावली 10.3

1. दो सदिशों $\vec{a}$ तथा $\vec{b}$ के परिमाण क्रमशः $\sqrt{3}$ एवं 2 हैं और $\vec{a} \cdot \vec{b}=\sqrt{6}$ है तो $\vec{a}$ तथा $\vec{b}$ के बीच का कोण ज्ञात कीजिए।

Show Answer

#missing

2. सदिशों $\hat{i}-2 \hat{j}+3 \hat{k}$ और $3 \hat{i}-2 \hat{j}+\hat{k}$ के बीच का कोण ज्ञात कीजिए।

Show Answer

#missing

3. सदिश $\hat{i}+\hat{j}$ पर सदिश $\hat{i}-\hat{j}$ का प्रक्षेप ज्ञात कीजिए।

Show Answer

#missing

4. सदिश $\hat{i}+3 \hat{j}+7 \hat{k}$ का, सदिश $7 \hat{i}-\hat{j}+8 \hat{k}$ पर प्रक्षेप ज्ञात कीजिए।

Show Answer

#missing

5. दर्शाइए कि दिए हुए निम्नलिखित तीन सदिशों में से प्रत्येक मात्रक सदिश है,

$\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k}), \frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k}), \quad \frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})$

यह भी दर्शाइए कि ये सदिश परस्पर एक दूसरे के लंबवत् हैं।

Show Answer

#missing

6. यदि $(\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=8$ और $|\vec{a}|=8|\vec{b}|$ हो तो $|\vec{a}|$ एवं $|\vec{b}|$ ज्ञात कीजिए।

Show Answer

#missing

7. $(3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})$ का मान ज्ञात कीजिए।

Show Answer

#missing

8. दो सदिशों $\vec{a}$ और $\vec{b}$ के परिमाण ज्ञात कीजिए, यदि इनके परिमाण समान है और इन के बीच का कोण $60^{\circ}$ है तथा इनका अदिश गुणनफल $\frac{1}{2}$ है।

Show Answer

#missing

9. यदि एक मात्रक सदिश $\vec{a}$, के लिए $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12$ हो तो $|\vec{x}|$ ज्ञात कीजिए।

Show Answer

#missing

10. यदि $\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$ और $\vec{c}=3 \hat{i}+\hat{j}$ इस प्रकार है कि $\vec{a}+\lambda \vec{b}, \vec{c}$ पर लंब है, तो $\lambda$ का मान ज्ञात कीजिए।

Show Answer

#missing

11. दर्शाइए कि दो शून्येतर सदिशों $\vec{a}$ और $\vec{b}$ के लिए $|\vec{a}| \vec{b}+|\vec{b}| \vec{a},|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ पर लंब है।

Show Answer

#missing

12. यदि $\vec{a} \cdot \vec{a}=0$ और $\vec{a} \cdot \vec{b}=0$, तो सदिश $\vec{b}$ के बारे में क्या निष्कर्ष निकाला जा सकता है?

Show Answer

#missing

13. यदि $\vec{a}, \vec{b}, \vec{c}$ मात्रक सदिश इस प्रकार है कि $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$ तो $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ का मान ज्ञात कीजिए।

Show Answer

#missing

14. यदि $\vec{a}=\overrightarrow{0}$ अथवा $\vec{b}=\overrightarrow{0}$, तब $\vec{a} \cdot \vec{b}=0$ परंतु विलोम का सत्य होना आवश्यक नहीं है। एक उदाहरण द्वारा अपने उत्तर की पुष्टि कीजिए।

Show Answer

#missing

15. यदि किसी त्रिभुज $\mathrm{ABC}$ के शीर्ष $\mathrm{A}, \mathrm{B}, \mathrm{C}$ क्रमशः $(1,2,3),(-1,0,0),(0,1,2)$ हैं तो $\angle \mathrm{ABC}$ ज्ञात कीजिए। [ $\angle \mathrm{ABC}$, सदिशों $\overrightarrow{\mathrm{BA}}$ एवं $\overrightarrow{\mathrm{BC}}$ के बीच का कोण है]

Show Answer

#missing

16. दर्शाइए कि बिंदु $\mathrm{A}(1,2,7), \mathrm{B}(2,6,3)$ और $\mathrm{C}(3,10,-1)$ संरेख हैं।

Show Answer

#missing

17. दर्शाइए कि सदिश $2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}$ और $3 \hat{i}-4 \hat{j}-4 \hat{k}$ एक समकोण त्रिभुज के शीर्षों की रचना करते हैं।

Show Answer

#missing

18. यदि शून्येतर सदिश $\vec{a}$ का परिमाण ’ $a$ ’ है और $\lambda$ एक शून्यतेर अदिश है तो $\lambda \vec{a}$ एक मात्रक सदिश है यदि

(A) $\lambda=1$

(B) $\lambda=-1$

(C) $a=|\lambda|$

(D) $a=1 /|\lambda|$

Show Answer

#missing

10.6.3 दो सदिशों का सदिश गुणनफल [Vector (or cross) product of two vectors]

परिच्छेद 10.2 में हमने त्रि-विमीय दक्षिणावर्ती समकोणिक निर्देशांक पद्धति की चर्चा की थी। इस पद्धति में धनात्मक $x$-अक्ष को वामावर्त घुमाकर धनात्मक $y$-अक्ष पर लाया जाता है तो धनात्मक $z$-अक्ष की दिशा में एक दक्षिणावर्ती (प्रामाणिक) पेंच अग्रगत हो जाती है [आकृति 10.22(i)]।

एक दक्षिणावर्ती निर्देशांक पद्धति में जब दाएँ हाथ की उँगलियों को धनात्मक $x$-अक्ष की दिशा से दूर धनात्मक $y$-अक्ष की तरफ़ कुंतल किया जाता है तो अँगूठा धनात्मक $z$-अक्ष की ओर संकेत करता [आकृति 10.22 (ii)] है।

आकृति 10.22

परिभाषा 3 दो शून्येतर सदिशों $\vec{a}$ तथा $\vec{b}$, का सदिश गुणनफल $\vec{a} \times \vec{b}$ से निर्दिष्ट किया जाता है और $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n}$ के रूप में परिभाषित किया जाता है जहाँ $\theta, \vec{a}$ और $\vec{b}$ के बीच का कोण है और $0 \leq \theta \leq \pi$ है। यहाँ $\hat{n}$ एक मात्रक सदिश है जो कि सदिश $\vec{a}$ और $\vec{b}$, दोनों पर लंब है। $-\hat{n}$ इस प्रकार $\vec{a}, \vec{b}$ तथा $\hat{n}$ एक दक्षिणावर्ती पद्धति को निर्मित करते हैं

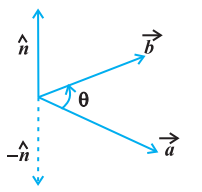
आकृति 10.23 (आकृति 10.23) अर्थात् दक्षिणावर्ती पद्धति को $\vec{a}$ से $\vec{b}$ की तरफ़ घुमाने पर यह $\hat{n}$ की दिशा में चलती है।

यदि $\vec{a}=\overrightarrow{0}$ अथवा $\vec{b}=\overrightarrow{0}$, तब $\theta$ परिभाषित नहीं है और इस स्थिति में हम $\vec{a} \times \vec{b}=\overrightarrow{0}$ परिभाषित करते हैं।

प्रेक्षण

1. $\vec{a} \times \vec{b}$ एक सदिश है।

2. मान लीजिए $\vec{a}$ और $\vec{b}$ दो शून्येतर सदिश हैं तब $\vec{a} \times \vec{b}=\overrightarrow{0}$ यदि और केवल यदि $\vec{a}$ और $\vec{b}$ एक दूसरे के समांतर (अथवा संरेख) हैं अर्थात्

$$ \vec{a} \times \vec{b}=\overrightarrow{0} \Leftrightarrow \vec{a} | \vec{b} $$

विशिष्टत: $\vec{a} \times \vec{a}=\overrightarrow{0}$ और $\vec{a} \times(-\vec{a})=\overrightarrow{0}$, क्योंकि प्रथम स्थिति में $\theta=0$ तथा द्वितीय स्थिति में $\theta=\pi$, जिससे दोनों ही स्थितियों में $\sin \theta$ का मान शून्य हो जाता है।

3. यदि $\theta=\frac{\pi}{2}$ तो $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|$

4. प्रेक्षण 2 और 3 के संदर्भ में परस्पर लंबवत् मात्रक सदिशों $\hat{i}, \hat{j}$ और $\hat{k}$ के लिए (आकृति 10.24), हम पाते हैं कि

$$ \begin{aligned} & \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0} \\ & \hat{i} \times \hat{j}=\hat{k}, \quad \hat{j} \times \hat{k}=\hat{i}, \hat{k} \times \hat{i}=\hat{j} \end{aligned} $$

आकृति 10.24

5. सदिश गुणनफल की सहायता से दो सदिशों $\vec{a}$ तथा $\vec{b}$ के बीच का कोण आकृति 10.24 $\theta$ निम्नलिखित रूप में प्राप्त होता है

$$ \sin \theta=\frac{|\vec{a} \times \vec{b}|}{|\vec{a}||\vec{b}|} $$

6. यह सर्वदा सत्य है कि सदिश गुणनफल क्रम विनिमय नहीं होता है क्योंकि $\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}$ वास्तव में $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n}$, जहाँ $\vec{a}, \vec{b}$ और $\hat{n}$ एक दक्षिणावर्ती पद्धति को निर्मित करते हैं अर्थात् $\theta, \vec{a}$ से $\vec{b}$ की तरफ चक्रीय क्रम होता है। आकृति 10.25(i) जबकि $\vec{b} \times \vec{a}=|\vec{a}||\vec{b}| \sin \theta \hat{n} _{1}$, जहाँ $\vec{b}, \vec{a}$ और $\hat{n} _{1}$ एक दक्षिणावर्ती पद्धति को निर्मित करते हैं अर्थात् $\theta, \vec{b}$ से $\vec{a}$ की ओर चक्रीय क्रम होता है आकृति 10.25(ii)।

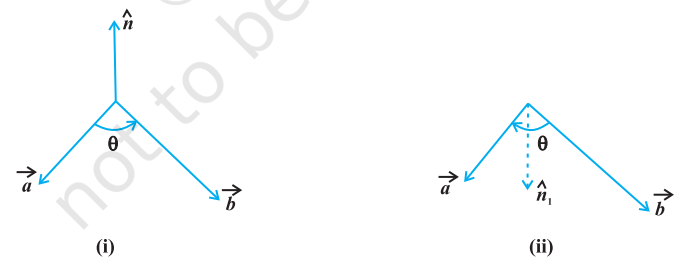
आकृति 10.25

अतः यदि हम यह मान लेते हैं कि $\vec{a}$ और $\vec{b}$ दोनों एक ही कागज़ के तल में हैं तो $\hat{n}$ और $\hat{n} _{1}$ दोनों कागज़ के तल पर लंब होंगे परंतु $\hat{n}$ कागज़ से ऊपर की तरफ़ दिष्ट होगा और $\hat{n} _{1}$ कागज़ से नीचे की तरफ़ दिष्ट होगा अर्थात् $\hat{n} _{1}=-\hat{n}$

इस प्रकार $$ \begin{aligned} \vec{a} \times \vec{b} & =|\vec{a}||\vec{b}| \sin \theta \hat{n} \\ & =-|\vec{a}||\vec{b}| \sin \theta \hat{n} _{1}=-\vec{b} \times \vec{a} \end{aligned} $$

7. प्रेक्षण 4 और 6 के संदर्भ में $$ \hat{j} \times \hat{i}=-\hat{k}, \hat{k} \times \hat{j}=-\hat{i} \text { और } \hat{i} \times \hat{k}=-\hat{j} \text { है। } $$

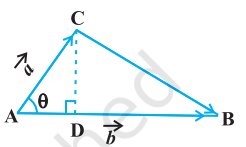
8. यदि $\vec{a}$ और $\vec{b}$ त्रिभुज की संलग्न भुजाओं को निरूपित करते हैं तो त्रिभुज का क्षेत्रफल $\frac{1}{2}|\vec{a} \times \vec{b}|$ के रूप में प्राप्त होता है।त्रिभुज के क्षेत्रफल की परिभाषा के अनुसार हम आकृति 10.26 से पाते हैं कि त्रिभुज $\mathrm{ABC}$ का क्षेत्रफल $=\frac{1}{2} \mathrm{AB} \cdot \mathrm{CD}$. परंतु $\mathrm{AB}=|\vec{b}|$ (दिया हुआ है) और $\mathrm{CD}=|\vec{a}| \sin \theta$ अतः त्रिभुज $\mathrm{ABC}$ का क्षेत्रफल $=\frac{1}{2}|\vec{b} | \vec{a}| \sin \theta=\frac{1}{2}|\vec{a} \times \vec{b}|$

आकृति 10.26

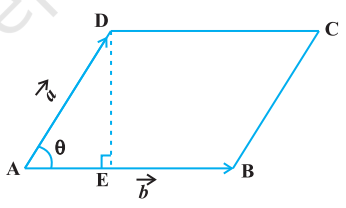
9. यदि $\vec{a}$ और $\vec{b}$ समांतर चतुर्भुज की संलग्न भुजाओं को निरूपित करते हैं तो समांतर चतुर्भुज का क्षेत्रफल $|\vec{a} \times \vec{b}|$ के रूप में प्राप्त होता है। आकृति 10.27 से हम पाते हैं कि समांतर चतुर्भज $\mathrm{ABCD}$ का क्षेत्रफल $=\mathrm{AB}$. DE. परंतु $\mathrm{AB}=|\vec{b}|$ (दिया हुआ है), और $\mathrm{DE}=|\vec{a}| \sin \theta$ अत: समांतर चतुर्भुज $\mathrm{ABCD}$ का क्षेत्रफल $=$ $|\vec{b} | \vec{a}| \sin \theta=|\vec{a} \times \vec{b}|$

आकृति 10.27

अब हम सदिश गुणनफल के दो महत्वपूर्ण गुणों को अभिव्यक्त करेंगे।

गुणधर्म 3 सदिश गुणनफल का योगफल पर वितरण नियम (Distributivity of vector product over addition) यदि $\vec{a}, \vec{b}$ और $\vec{c}$ तीन सदिश हैं और $\lambda$ एक अदिश है तो

(i) $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

(ii) $\lambda(\vec{a} \times \vec{b})=(\lambda \vec{a}) \times \vec{b}=\vec{a} \times(\lambda \vec{b})$

मान लीजिए दो सदिश $\vec{a}$ और $\vec{b}$ घटक रूप में क्रमशः $a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ और $b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}$ दिए हुए हैं तब उनका सदिश गुणनफल

$\vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ a _{1} & a _{2} & a _{3} \\ b _{1} & b _{2} & b _{3}\end{array}\right|$ द्वारा दिया जा सकता है।

व्याख्या हम पाते हैं

$$ \begin{aligned} \vec{a} \times \vec{b}= & \left(a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}\right) \times\left(b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}\right) \\ = & a _{1} b _{1}(\hat{i} \times \hat{i})+a _{1} b _{2}(\hat{i} \times \hat{j})+a _{1} b _{3}(\hat{i} \times \hat{k})+a _{2} b _{1}(\hat{j} \times \hat{i}) \\ & +a _{2} b _{2}(\hat{j} \times \hat{j})+a _{2} b _{3}(\hat{j} \times \hat{k}) \\ & +a _{3} b _{1}(\hat{k} \times \hat{i})+a _{3} b _{2}(\hat{k} \times \hat{j})+a _{3} b _{3}(\hat{k} \times \hat{k}) \\ = & a _{1} b _{2}(\hat{i} \times \hat{j})-a _{1} b _{3}(\hat{k} \times \hat{i})-a _{2} b _{1}(\hat{i} \times \hat{j}) \\ & +a _{2} b _{3}(\hat{j} \times \hat{k})+a _{3} b _{1}(\hat{k} \times \hat{i})-a _{3} b _{2}(\hat{j} \times \hat{k}) \end{aligned} $$

क्योंकि

( $\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0$ और $\hat{i} \times \hat{k}=-\hat{k} \times \hat{i}, \hat{j} \times \hat{i}=-\hat{i} \times \hat{j}$ और $\hat{k} \times \hat{j}=-\hat{j} \times \hat{k}$ )

$$ \begin{aligned} &=a _{1} b _{2} \hat{k}-a _{1} b _{3} \hat{j}-a _{2} b _{1} \hat{k}+a _{2} b _{3} \hat{i}+a _{3} b _{1} \hat{j}-a _{3} b _{2} \hat{i} \\ &(\text { क्योंकि } \hat{i} \times \hat{j}=\hat{k}, \hat{j} \times \hat{k}=\hat{i} \text { और } \hat{k} \times \hat{i}=\hat{j}) \\ &=\left(a _{2} b _{3}-a _{3} b _{2}\right) \hat{i}-\left(a _{1} b _{3}-a _{3} b _{1}\right) \hat{j}+\left(a _{1} b _{2}-a _{2} b _{1}\right) \hat{k} \\ &=\left|\begin{array}{lll} \hat{i} & \hat{j} & \hat{k} \\ a _{1} & a _{2} & a _{3} \\ b _{1} & b _{2} & b _{3} \end{array}\right| \end{aligned} $$

उदाहरण 22 यदि $\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}$ और $\vec{b}=3 \hat{i}+5 \hat{j}-2 \hat{k}$, तो $|\vec{a} \times \vec{b}|$ ज्ञात कीजिए।

हल यहाँ

$$ \begin{aligned} \vec{a} \times \vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 3 \\ 3 & 5 & -2 \end{array}\right| \\ & =\hat{i}(-2-15)-(-4-9) \hat{j}+(10-3) \hat{k}=-17 \hat{i}+13 \hat{j}+7 \hat{k} \end{aligned} $$

अत: $\quad|\vec{a} \times \vec{b}|=\sqrt{(-17)^{2}+(13)^{2}+(7)^{2}}=\sqrt{507}$

उदाहरण 23 सदिश $(\vec{a}+\vec{b})$ और $(\vec{a}-\vec{b})$ में से प्रत्येक के लंबवत् मात्रक सदिश ज्ञात कीजिए जहाँ $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \quad \vec{b}=\hat{i}+2 \hat{j}+3 \hat{k}$ हैं।

हल हम पाते हैं कि $\vec{a}+\vec{b}=2 \hat{i}+3 \hat{j}+4 \hat{k}$ और $\vec{a}-\vec{b}=-\hat{j}-2 \hat{k}$

एक सदिश, जो $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ दोनो पर लंब है, निम्नलिखित द्वारा प्रदत्त है

अब $$ (\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 0 & -1 & -2 \end{array}\right|=-2 \hat{i}+4 \hat{j}-2 \hat{k} \quad(=\vec{c}, \text { मान लीजिए }) $$

$$ |\vec{c}|=\sqrt{4+16+4}=\sqrt{24}=2 \sqrt{6} $$

अतः अभीष्ट मात्रक सदिश $$ \frac{\vec{c}}{|\vec{c}|}=\frac{-1}{\sqrt{6}} \hat{i}+\frac{2}{\sqrt{6}} \hat{j}-\frac{1}{\sqrt{6}} \hat{k} \text { है। } $$

टिप्पणी किसी तल पर दो लंबवत् दिशाएँ होती हैं। अतः $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ पर दूसरा लंबवत् मात्रक सदिश $\frac{1}{\sqrt{6}} \hat{i}-\frac{2}{\sqrt{6}} \hat{j}+\frac{1}{\sqrt{6}} \hat{k}$ होगा। परंतु यह $(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$ का एक परिणाम है।

उदाहरण 24 एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष बिंदु $\mathrm{A}(1,1,1), \mathrm{B}(1,2,3)$ और $\mathrm{C}(2,3,1)$ हैं।

हल हम पाते हैं कि $\overrightarrow{\mathrm{AB}}=\hat{j}+2 \hat{k}$ और $\overrightarrow{\mathrm{AC}}=\hat{i}+2 \hat{j}$. दिए हुए त्रिभुज का क्षेत्रफल $\frac{1}{2}|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|$ है $\mid$

अब $$ \overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{array}\right|=-4 \hat{i}+2 \hat{j}-\hat{k} $$

इसलिए $$ |\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|=\sqrt{16+4+1}=\sqrt{21} $$

अतः अभीष्ट क्षेत्रफल $\frac{1}{2} \sqrt{21}$ है।

उदाहरण 25 उस समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी संलग्न भुजाएँ $\vec{a}=3 \hat{i}+\hat{j}+4 \hat{k}$ और $\vec{b}=\hat{i}-\hat{j}+\hat{k}$ द्वारा दी गई हैं।

हल किसी समांतर चतुर्भुज की संलग्न भुजाएँ $\vec{a}$ और $\vec{b}$ हैं तो उसका क्षेत्रफल $|\vec{a} \times \vec{b}|$ द्वारा प्राप्त होता है।

अब $$ \vec{a} \times \vec{b}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 4 \\ 1 & -1 & 1 \end{array}\right|=5 \hat{i}+\hat{j}-4 \hat{k} $$

इसलिए $$ |\vec{a} \times \vec{b}|=\sqrt{25+1+16}=\sqrt{42} $$

इस प्रकार आवश्यक क्षेत्रफल $\sqrt{42}$ है।

प्रश्नावली 10.4

1. यदि $\vec{a}=\hat{i}-7 \hat{j}+7 \hat{k}$ और $\vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k}$ तो $|\vec{a} \times \vec{b}|$ ज्ञात कीजिए।

Show Answer

#missing

2. सदिश $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ की लंब दिशा में मात्रक सदिश ज्ञात कीजिए जहाँ $\vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k}$ और $\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}$ है।

Show Answer

#missing

3. यदि एक मात्रक सदिश $\vec{a}, \hat{i}$ के साथ $\frac{\pi}{3}, \hat{j}$ के साथ $\frac{\pi}{4}$ और $\hat{k}$ के साथ एक न्यून कोण $\theta$ बनाता है तो $\theta$ का मान ज्ञात कीजिए और इसकी सहायता से $\vec{a}$ के घटक भी ज्ञात कीजिए।

Show Answer

#missing

4. दर्शाइए कि

$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})$

Show Answer

#missing

5. $\lambda$ और $\mu$ ज्ञात कीजिए, यदि $(2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{0}$

Show Answer

#missing

6. दिया हुआ है कि $\vec{a} \cdot \vec{b}=0$ और $\vec{a} \times \vec{b}=\overrightarrow{0}$. सदिश $\vec{a}$ और $\vec{b}$ के बारे में आप क्या निष्कर्ष निकाल सकते हैं?

Show Answer

#missing

7. मान लीजिए सदिश $\vec{a}, \vec{b}, \vec{c}$ क्रमश: $a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}, b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}, c _{1} \hat{i}+c _{2} \hat{j}+c _{3} \hat{k}$ के रूप में दिए हुए हैं तब दर्शाइए कि $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

Show Answer

#missing

8. यदि $\vec{a}=\overrightarrow{0}$ अथवा $\vec{b}=\overrightarrow{0}$ तब $\vec{a} \times \vec{b}=\overrightarrow{0}$ होता है। क्या विलोम सत्य है? उदाहरण सहित अपने उत्तर की पुष्टि कीजिए।

Show Answer

#missing

9. एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष $\mathrm{A}(1,1,2), \mathrm{B}(2,3,5)$ और $\mathrm{C}(1,5,5)$ हैं।

Show Answer

#missing

10. एक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी संलग्न भुजाएँ सदिश $\vec{a}=\hat{i}-\hat{j}+3 \hat{k}$ और $\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}$ द्वारा निर्धारित हैं।

Show Answer

#missing

11. मान लीजिए सदिश $\vec{a}$ और $\vec{b}$ इस प्रकार हैं कि $|\vec{a}|=3$ और $|\vec{b}|=\frac{\sqrt{2}}{3}$, तब $\vec{a} \times \vec{b}$ एक मात्रक सदिश है यदि $\vec{a}$ और $\vec{b}$ के बीच का कोण है:

(A) $\pi / 6$

(B) $\pi / 4$

(C) $\pi / 3$

(D) $\pi / 2$

Show Answer

#missing

12. एक आयत के शीर्षों $\mathrm{A}, \mathrm{B}, \mathrm{C}$ और $\mathrm{D}$ जिनके स्थिति सदिश क्रमशः $-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$ और $-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$, हैं का क्षेत्रफल है:

(A) $\frac{1}{2}$

(B) 1

(C) 2

(D) 4

Show Answer

#missing

विविध उदाहरण

उदाहरण 26 $\mathrm{XY}$-तल में सभी मात्रक सदिश लिखिए।

हल मान लीजिए कि $\vec{r}=x \hat{i}+y \hat{j}, \mathrm{XY}$-तल में एक मात्रक सदिश है (आकृति 10.28)। तब आकृति के अनुसार हम पाते हैं कि $x=\cos \theta$ और $y=\sin \theta$ (क्योंकि $|\vec{r}|=1$ ). इसलिए हम सदिश $\vec{r}$ को, के रूप में लिख सकते हैं।

$$ \begin{equation*} \vec{r}(=\overrightarrow{\mathrm{OP}})=\cos \theta \hat{i}+\sin \theta \hat{j} \tag{1} \end{equation*} $$

स्पष्टत: $$ |\vec{r}|=\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}=1 $$

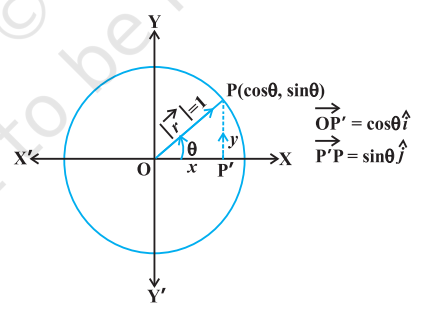
आकृति 10.28

जैसे-जैसे $\theta, 0$ से $2 \pi$, तक परिवर्तित होता है बिंदु $\mathrm{P}$ (आकृति 10.28) वामावर्त दिशा में वृत $x^{2}+y^{2}=1$ का अनुरेखण करता है और इसमें सभी संभावित दिशाएँ सम्मिलित हैं। अतः (1) से XYतल में प्रत्येक मात्रक सदिश प्राप्त होता है।

उदाहरण 27 यदि बिंदुओं $\mathrm{A}, \mathrm{B}, \mathrm{C}$ और $\mathrm{D}$, के स्थिति सदिश क्रमशः $\hat{i}+\hat{j}+\hat{k}, 2 \hat{i}+5 \hat{j}$, $3 \hat{i}+2 \hat{j}-3 \hat{k}$ और $\hat{i}-6 \hat{j}-\hat{k}$ है, तो सरल रेखाओं $\mathrm{AB}$ तथा $\mathrm{CD}$ के बीच का कोण ज्ञात कीजिए। निगमन कीजिए कि $\mathrm{AB}$ और $\mathrm{CD}$ संरेख हैं।

हल नोट कीजिए कि यदि $\theta, \mathrm{AB}$ और $\mathrm{CD}$, के बीच का कोण है तो $\theta, \overrightarrow{\mathrm{AB}}$ और $\overrightarrow{\mathrm{CD}}$ के बीच का भी कोण है।

अब $$ \begin{aligned} \overrightarrow{\mathrm{AB}} & =\mathrm{B} \text { का स्थिति सदिश }-\mathrm{A} \text { का स्थिति सदिश } \\ & =(2 \hat{i}+5 \hat{j})-(\hat{i}+\hat{j}+\hat{k})=\hat{i}+4 \hat{j}-\hat{k} \end{aligned} $$

इसलिए $$ |\overrightarrow{\mathrm{AB}}|=\sqrt{(1)^{2}+(4)^{2}+(-1)^{2}}=3 \sqrt{2} $$

इसी प्रकार $\overrightarrow{\mathrm{CD}}=-2 \hat{i}-8 \hat{j}+2 \hat{k}$ और $|\overrightarrow{\mathrm{CD}}|=6 \sqrt{2}$

अत: $$ \begin{aligned} \cos \theta & =\frac{\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{CD}}}{|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{CD}}|} \\ & =\frac{1(-2)+4(-8)+(-1)(2)}{(3 \sqrt{2})(6 \sqrt{2})}=\frac{-36}{36}=-1 \end{aligned} $$

क्योंकि $0 \leq \theta \leq \pi$, इससे प्राप्त होता है कि $\theta=\pi$. यह दर्शाता है कि $\mathrm{AB}$ तथा $\mathrm{CD}$ एक दूसरे के संरेख हैं।

विकल्पतः $\overrightarrow{\mathrm{AB}}=-\frac{1}{2} \overrightarrow{\mathrm{CD}}$, इससे कह सकते कि $\overrightarrow{\mathrm{AB}}$ और $\overrightarrow{\mathrm{CD}}$ संरेख सदिश हैं।

उदाहरण 28 मान लीजिए $\vec{a}, \vec{b}$ और $\vec{c}$ तीन सदिश इस प्रकार हैं कि $|\vec{a}|=3,|\vec{b}|=4,|\vec{c}|=5$ और इनमें से प्रत्येक, अन्य दो सदिशों के योगफल पर लंबवत् हैं तो, $|\vec{a}+\vec{b}+\vec{c}|$ ज्ञात कीजिए।

हल दिया हुआ है कि $\vec{a} \cdot(\vec{b}+\vec{c})=0, \vec{b} \cdot(\vec{c}+\vec{a})=0, \vec{c} \cdot(\vec{a}+\vec{b})=0$

अब $$ \begin{aligned} |\vec{a}+\vec{b}+\vec{c}|^{2}= & (\vec{a}+\vec{b}+\vec{c}) \cdot(\vec{a}+\vec{b}+\vec{c}) \\ = & \vec{a} \cdot \vec{a}+\vec{a} \cdot(\vec{b}+\vec{c})+\vec{b} \cdot \vec{b}+\vec{b} \cdot(\vec{a}+\vec{c}) \\ & +\vec{c} \cdot(\vec{a}+\vec{b})+\vec{c} \cdot \vec{c} \\ = & |\vec{a}|^{2}+|\vec{b}|^{2}+|\vec{c}|^{2} \\ = & 9+16+25=50 \end{aligned} $$

इसलिए $$ |\vec{a}+\vec{b}+\vec{c}|=\sqrt{50}=5 \sqrt{2} $$

उदाहरण 29 तीन सदिश $\vec{a}, \vec{b}$ और $\vec{c}$ प्रतिबंध $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$ को संतुष्ट करते हैं। यदि $|\vec{a}|=3,|\vec{b}|=4$ और $|\vec{c}|=2$ तो राशि $\mu=\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ का मान ज्ञात कीजिए।

हल क्योंकि $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$, इसलिए हम पाते हैं कि

अथवा $$ \begin{aligned} \vec{a} \cdot(\vec{a}+\vec{b}+\vec{c}) & =0 \\ \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} & =0 \\ \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} & =-|\vec{a}|^{2}=-9 \\ \vec{b} \cdot(\vec{a}+\vec{b}+\vec{c}) & =0 \end{aligned} $$

इसलिए $$ \begin{equation*} \vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}=-|\vec{b}|^{2}=-16 \tag{2} \end{equation*} $$ $$ \begin{equation*} \vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}=-4 \tag{3} \end{equation*} $$

(1), (2) और (3) को जोड़ने पर हम पाते हैं कि $$ \begin{array}{r} 2(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{a} \cdot \vec{c})=-29 \\ 2 \mu=-29, \text { i.e., } \mu=\frac{-29}{2} \end{array} $$

उदाहरण 30 यदि परस्पर लंबवत् मात्रक सदिशों $\hat{i}, \hat{j}$ और $\hat{k}$, की दक्षिणावर्ती पद्धति के सापेक्ष $\vec{\alpha}=3 \hat{i}-\hat{j}, \vec{\beta}=2 \hat{i}+\hat{j}-3 \hat{k}$, तो $\vec{\beta}$ को $\vec{\beta}=\vec{\beta} _{1}+\vec{\beta} _{2}$ के रूप में अभिव्यक्त कीजिए जहाँ $\vec{\beta} _{1}$, $\vec{\alpha}$ के समांतर है और $\vec{\beta} _{2}, \vec{\alpha}$ के लंबवत् है।

हल मान लीजिए कि $\vec{\beta} _{1}=\lambda \vec{\alpha}, \lambda$ एक अदिश है अर्थात् $\vec{\beta} _{1}=3 \lambda \hat{i}-\lambda \hat{j}$

अब $$ \vec{\beta} _{2}=\vec{\beta}-\vec{\beta} _{1}=(2-3 \lambda) \hat{i}+(1+\lambda) \hat{j}-3 \hat{k} $$

क्योंकि $$ \vec{\beta} _{2}, \vec{\alpha} \text { पर लंब है इसलिए } \vec{\alpha} \cdot \vec{\beta} _{2}=0 $$

अर्थात् $$ 3(2-3 \lambda)-(1+\lambda)=0 $$

अथवा $$ \lambda=\frac{1}{2} $$

इसलिए $$ \vec{\beta} _{1}=\frac{3}{2} \hat{i}-\frac{1}{2} \hat{j} \text { और } \quad \vec{\beta} _{2}=\frac{1}{2} \hat{i}+\frac{3}{2} \hat{j}-3 \hat{k} $$

अध्याय 10 पर विविध प्रश्नावली

1. XY-तल में, $x$-अक्ष की धनात्मक दिशा के साथ वामावर्त दिशा में $30^{\circ}$ का कोण बनाने वाला मात्रक सदिश लिखिए।

Show Answer

#missing

2. बिंदु $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ को मिलाने वाले सदिश के अदिश घटक और परिमाण ज्ञात कीजिए।

Show Answer

#missing

3. एक लड़की पश्चिम दिशा में $4 \mathrm{~km}$ चलती है। उसके पश्चात् वह उत्तर से $30^{\circ}$ पश्चिम की दिशा में $3 \mathrm{~km}$ चलती है और रूक जाती है। प्रस्थान के प्रारंभिक बिंदु से लड़की का विस्थापन ज्ञात कीजिए।

Show Answer

#missing

4. यदि $\vec{a}=\vec{b}+\vec{c}$, तब क्या यह सत्य है कि $|\vec{a}|=|\vec{b}|+|\vec{c}|$ ? अपने उत्तर की पुष्टि कीजिए।

Show Answer

#missing

5. $x$ का वह मान ज्ञात कीजिए जिसके लिए $x(\hat{i}+\hat{j}+\hat{k})$ एक मात्रक सदिश है।

Show Answer

#missing

6. सदिशों $\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}$ और $\vec{b}=\hat{i}-2 \hat{j}+\hat{k}$ के परिणामी के समांतर एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 5 इकाई है।

Show Answer

#missing

7. यदि $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k}$ और $\vec{c}=\hat{i}-2 \hat{j}+\hat{k}$, तो सदिश $2 \vec{a}-\vec{b}+3 \vec{c}$ के समांतर एक मात्रक सदिश ज्ञात कीजिए।

Show Answer

#missing

8. दर्शाइए कि बिंदु $\mathrm{A}(1,-2,-8), \mathrm{B}(5,0,-2)$ और $\mathrm{C}(11,3,7)$ संरेख है और $\mathrm{B}$ द्वारा $\mathrm{AC}$ को विभाजित करने वाला अनुपात ज्ञात कीजिए।

Show Answer

#missing

9. दो बिंदुओं $\mathrm{P}(2 \vec{a}+\vec{b})$ और $\mathrm{Q}(\vec{a}-3 \vec{b})$ को मिलाने वाली रेखा को $1: 2$ के अनुपात मे बाह्य विभाजित करने वाले बिंदु $\mathrm{R}$ का स्थिति सदिश ज्ञात कीजिए। यह भी दर्शाइए कि बिंदु $\mathrm{P}$ रेखाखंड $\mathrm{RQ}$ का मध्य बिंदु है।

Show Answer

#missing

10. एक समांतर चतुर्भुज की संलग्न भुजाएँ $2 \hat{i}-4 \hat{j}+5 \hat{k}$ और $\hat{i}-2 \hat{j}-3 \hat{k}$ हैं। इसके विकर्ण के समांतर एक मात्रक सदिश ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए।

Show Answer

#missing

11. दर्शाइए कि $\mathrm{OX}, \mathrm{OY}$ एवं $\mathrm{OZ}$ अक्षों के साथ बराबर झुके हुए सदिश की दिक्-कोसाइन कोज्याएँ $\pm\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)$ है।

Show Answer

#missing

12. मान लीजिए $\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}, \vec{b}=3 \hat{i}-2 \hat{j}+7 \hat{k}$ और $\vec{c}=2 \hat{i}-\hat{j}+4 \hat{k}$. एक ऐसा सदिश $\vec{d}$ ज्ञात कीजिए जो $\vec{a}$ और $\vec{b}$ दोनों पर लंब है और $\vec{c} \cdot \vec{d}=15$

Show Answer

#missing

13. सदिश $\hat{i}+\hat{j}+\hat{k}$ का, सदिशों $2 \hat{i}+4 \hat{j}-5 \hat{k}$ और $\lambda \hat{i}+2 \hat{j}+3 \hat{k}$ के योगफल की दिशा में मात्रक सदिश के साथ अदिश गुणनफल 1 के बराबर है तो $\lambda$ का मान ज्ञात कीजिए।

Show Answer

#missing

14. यदि $\vec{a}, \vec{b}, \overrightarrow{\mathrm{c}}$ समान परिमाणों वाले परस्पर लंबवत् सदिश हैं तो दर्शाइए कि सदिश $\vec{a}+\vec{b}+\vec{c}$ सदिशों $\vec{a}, \vec{b}$ तथा $\vec{c}$ के साथ बराबर झुका हुआ है।

Show Answer

#missing

15. सिद्ध कीजिए कि $(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}$, यदि और केवल यदि $\vec{a}, \vec{b}$ लंबवत् हैं। यह दिया हुआ है कि $\vec{a} \neq \overrightarrow{0}, \vec{b} \neq \overrightarrow{0}$

Show Answer

#missing

16 से 19 तक के प्रश्नों में सही उत्तर का चयन कीजिए।

16. यदि दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो $\vec{a} \cdot \vec{b} \geq 0$ होगा यदि:

(A) $0<\theta<\frac{\pi}{2}$

(B) $0 \leq \theta \leq \frac{\pi}{2}$

(C) $0<\theta<\pi$

(D) $0 \leq \theta \leq \pi$

Show Answer

#missing

17. मान लीजिए $\vec{a}$ और $\vec{b}$ दो मात्रक सदिश हैं और उनके बीच का कोण $\theta$ है तो $\vec{a}+\vec{b}$ एक मात्रक सदिश है यदि:

(A) $\theta=\frac{\pi}{4}$

(B) $\theta=\frac{\pi}{3}$

(C) $\theta=\frac{\pi}{2}$

(D) $\theta=\frac{2 \pi}{3}$

Show Answer

#missing

18. $\hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})+\hat{k} \cdot(\hat{i} \times \hat{j})$ का मान है

(A) 0

(B) -1

(C) 1

(D) 3

Show Answer

#missing

19. यदि दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो $|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|$ जब $\theta$ बराबर है:

(A) 0

(B) $\frac{\pi}{4}$

(C) $\frac{\pi}{2}$

(D) $\pi$

Show Answer

#missing

सारांश

• एक बिंदु $\mathrm{P}(x, y, z)$ की स्थिति सदिश $\overrightarrow{\mathrm{OP}}(=\vec{r})=x \hat{i}+y \hat{j}+z \hat{k}$ है और परिमाण $\sqrt{x^{2}+y^{2}+z^{2}}$ है।

• एक सदिश के अदिश घटक इसके दिक्-अनुपात कहलाते हैं और क्रमागत अक्षों के साथ इसके प्रक्षेप को निरूपित करते हैं।

• एक सदिश का परिमाण $(r)$, दिक्-अनुपात $a, b, c$ और दिक्-कोसाइन $(l, m, n)$ निम्नलिखित रूप में संबंधित हैं:

$$ l=\frac{a}{r}, \quad m=\frac{b}{r}, n=\frac{c}{r} $$

• त्रिभुज की तीनों भुजाओं को क्रम में लेने पर उनका सदिश योग $\overrightarrow{0}$ है।

• दो सह-आदिम सदिशों का योग एक ऐसे समांतर चतुर्भुज के विकर्ण से प्राप्त होता है जिसकी संलग्न भुजाएँ दिए हुए सदिश हैं।

• एक सदिश का अदिश $\lambda$ से गुणन इसके परिमाण को $|\lambda|$ के गुणज में परिवर्तित कर देता है और $\lambda$ का मान धनात्मक अथवा ऋणात्मक होने के अनुसार इसकी दिशा को समान अथवा विपरीत रखता है।

• दिए हुए सदिश $\vec{a}$ के लिए सदिश $\hat{a}=\frac{\vec{a}}{|\vec{a}|}, \vec{a}$ की दिशा में मात्रक सदिश है।

• बिदुओं $\mathrm{P}$ और $\mathrm{Q}$ जिनके स्थिति सदिश क्रमशः $\vec{a}$ और $\vec{b}$ हैं, को मिलाने वाली रेखा को $m: n$ के अनुपात में विभाजित करने वाले बिंदु $\mathrm{R}$ का स्थिति सदिश (i) $\frac{n \vec{a}+m \vec{b}}{m+n}$ अंतः विभाजन पर (ii) $\frac{m \vec{b}-n \vec{a}}{m-n}$ बाह्य विभाजन पर, के रूप में प्राप्त होता है।

• दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो उनका अदिश गुणनफल $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$ के रूप में प्राप्त होता है। यदि $\vec{a} \cdot \vec{b}$ दिया हुआ है तो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण ’ $\theta$ ‘, $\cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$ से प्राप्त होता है।

• यदि दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो उनका सदिश गुणनफल $\vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n}$ के रूप में प्राप्त होता है। जहाँ $\hat{n}$ एक ऐसा मात्रक सदिश है जो $\vec{a}$ और $\vec{b}$ को सम्मिलित करने वाले तल के लंबवत् है तथा $\vec{a}, \vec{b}$ और $\hat{n}$ दक्षिणावर्ती समकोणिक निर्देशांक पद्धति को निर्मित करते हैं।

• यदि $\vec{a}=a _{1} \hat{i}+a _{2} \hat{j}+a _{3} \hat{k}$ तथा $\vec{b}=b _{1} \hat{i}+b _{2} \hat{j}+b _{3} \hat{k}$ और $\lambda$ एक अदिश है तो $$ \begin{aligned} \vec{a}+\vec{b} & =\left(a _{1}+b _{1}\right) \hat{i}+\left(a _{2}+b _{2}\right) \hat{j}+\left(a _{3}+b _{3}\right) \hat{k} \\ \lambda \vec{a} & =\left(\lambda a _{1}\right) \hat{i}+\left(\lambda a _{2}\right) \hat{j}+\left(\lambda a _{3}\right) \hat{k} \\ \vec{a} \cdot \vec{b} & =a _{1} b _{1}+a _{2} b _{2}+a _{3} b _{3} \\ \text { और } \quad \vec{a} \times \vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ a _{1} & b _{1} & c _{1} \\ a _{2} & b _{2} & c _{2} \end{array}\right| \end{aligned} $$

ऐतिहासिक पृष्ठभूमि

सदिश शब्द का व्युत्पन्न लैटिन भाषा के एक शब्द वेक्टस (vectus) से हुआ है जिसका अर्थ है हस्तगत करना। आधुनिक सदिश सिद्धांत के भ्रूणीय विचार की तिथि सन् 1800 के आसपास मानी जाती है, जब Caspar Wessel (1745-1818 ई.) और Jean Robert Argand (1768-1822ई.) ने इस बात का वर्णन किया कि एक निर्देशांक तल में किसी दिष्ट रेखाखंड की सहायता से एक सम्मिश्र संख्या $a+i b$ का ज्यामितीय अर्थ निर्वचन कैसे किया जा सकता है। एक आयरिश गणितज्ञ, William Rowen Hamilton (1805-1865 ई.) ने अपनी पुस्तक, “Lectures on Quaternions” (1853 ई.) में दिष्ट रेखाखंड के लिए सदिश शब्द का प्रयोग सबसे पहले किया था। चतुष्टयीयों (quaternians) [कुछ निश्चित बीजीय नियमों का पालन करते हुए $a+b \hat{i}+c \hat{j}+d \hat{k}, \hat{i}, \hat{j}, \hat{k}$ के रूप वाले चार वास्तविक संख्याओं का समुच्चय] की हैमिल्टन विधि सदिशों को त्रि-विमीय अंतरिक्ष में गुणा करने की समस्या का एक हल था। तथापि हम यहाँ इस बात का जिक्र अवश्य करेंगे कि सदिश की संकल्पना और उनके योगफल का विचार बहुत- दिनों पहले से Plato (384-322 ईसा पूर्व) के एक शिष्य एवं यूनानी दार्शानिक और वैज्ञानिक Aristotle (427-348 ईसा पूर्व) के काल से ही था। उस समय इस जानकारी की कल्पना थी कि दो अथवा अधिक बलों की संयुक्त क्रिया उनको समांतर चतुर्भुज के नियमानुसार योग करने पर प्राप्त की जा सकती है। बलों के संयोजन का सही नियम, कि बलों का योग सदिश रूप में किया जा सकता है, की खोज Sterin Simon(1548-1620ई.) द्वारा लंबवत् बलों की स्थिति में की गई। सन् 1586 में उन्होंने अपनी शोधपुस्तक, “DeBeghinselen der Weeghconst” (वजन करने की कला के सिद्धांत) में बलों के योगफल के ज्यामितीय सिद्धांत का विश्लेषण किया था जिसके कारण यांत्रिकी के विकास में एक मुख्य परिवर्तन हुआ। परंतु इसके बाद भी सदिशों की व्यापक संकल्पना के निर्माण में 200 वर्ष लग गए।

सन् 1880 में एक अमेरिकी भौतिक शास्त्री एवं गणितज्ञ Josaih Willard Gibbs (1839-1903 ई.) और एक अंग्रेज अभियंता Oliver Heaviside (1850-1925 ई.) ने एक चतुष्टयी के वास्तविक (अदिश) भाग को काल्पनिक (सदिश) भाग से पृथक् करते हुए सदिश विश्लेषण का सृजन किया था। सन् 1881 और 1884 में Gibbs ने “Entitled Element of Vector Analysis” नामक एक शोध पुस्तिका छपवाई। इस पुस्तक में सदिशों का एक क्रमबद्ध एवं संक्षिप्त विवरण दिया हुआ था। तथापि सदिशों के अनुप्रयोग का निरूपण करने की कीर्ति D. Heaviside और P.G. Tait (1831-1901 ई.) को प्राप्त है जिन्होंने इस विषय के लिए सार्थक योगदान दिया है।