Chapter 06 Triangles
6.1 Introduction
You are familiar with triangles and many of their properties from your earlier classes. In Class IX, you have studied congruence of triangles in detail. Recall that two figures are said to be congruent, if they have the same shape and the same size. In this chapter, we shall study about those figures which have the same shape but not necessarily the same size. Two figures having the same shape (and not necessarily the same size) are called similar figures. In particular, we shall discuss the similarity of triangles and apply this knowledge in giving a simple proof of Pythagoras Theorem learnt earlier.

Can you guess how heights of mountains (say Mount Everest) or distances of some long distant objects (say moon) have been found out? Do you think these have been measured directly with the help of a measuring tape? In fact, all these heights and distances have been found out using the idea of indirect measurements, which is based on the principle of similarity of figures (see Example 7 , Q. 15 of Exercise 6.3 and also Chapters 8 and 9 of this book).
6.2 Similar Figures
In Class IX, you have seen that all circles with the same radii are congruent, all squares with the same side lengths are congruent and all equilateral triangles with the same side lengths are congruent.

Fig. 6.1
Now consider any two (or more) circles [see Fig. 6.1 (i)]. Are they congruent? Since all of them do not have the same radius, they are not congruent to each other. Note that some are congruent and some are not, but all of them have the same shape. So they all are, what we call, similar. Two similar figures have the same shape but not necessarily the same size. Therefore, all circles are similar. What about two (or more) squares or two (or more) equilateral triangles [see Fig. 6.1 (ii) and (iii)]? As observed in the case of circles, here also all squares are similar and all equilateral triangles are similar.
From the above, we can say that all congruent figures are similar but the similar figures need not be congruent.
Can a circle and a square be similar? Can a triangle and a square be similar? These questions can be answered by just looking at the figures (see Fig. 6.1). Evidently these figures are not similar. (Why?)

Fig. 6.2
What can you say about the two quadrilaterals

Fig. 6.3
You will at once say that they are the photographs of the same monument (Taj Mahal) but are in different sizes. Would you say that the three photographs are similar? Yes,they are.
What can you say about the two photographs of the same size of the same person one at the age of 10 years and the other at the age of 40 years? Are these photographs similar? These photographs are of the same size but certainly they are not of the same shape. So, they are not similar.
What does the photographer do when she prints photographs of different sizes from the same negative? You must have heard about the stamp size, passport size and postcard size photographs. She generally takes a photograph on a small size film, say of 35 mm size and then enlarges it into a bigger size, say 45 mm (or 55 mm ). Thus, if we consider any line segment in the smaller photograph (figure), its corresponding line segment in the bigger photograph (figure) will be
Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
Note that the same ratio of the corresponding sides is referred to as the scale factor (or the Representative Fraction) for the polygons. You must have heard that world maps (i.e., global maps) and blue prints for the construction of a building are prepared using a suitable scale factor and observing certain conventions.
In order to understand similarity of figures more clearly, let us perform the following activity:
Activity 1 : Place a lighted bulb at a point
on the ceiling and directly below it a table in your classroom. Let us cut a polygon, say a quadrilateral , from a plane cardboard and place this cardboard parallel to the ground between the lighted bulb and the table. Then a shadow of ABCD is cast on the table. Mark the outline of this shadow as (see Fig.6.4).
Note that the quadrilateral

Fig. 6.4
So, quadrilateral
Here, you can also note that vertex
(i)
(ii)
This again emphasises that two polygons of the same number of sides are similar, if (i) all the corresponding angles are equal and (ii) all the corresponding sides are in the same ratio (or proportion).
From the above, you can easily say that quadrilaterals

Fig. 6.5
Remark : You can verify that if one polygon is similar to another polygon and this second polygon is similar to a third polygon, then the first polygon is similar to the third polygon.
You may note that in the two quadrilaterals (a square and a rectangle) of Fig. 6.6, corresponding angles are equal, but their corresponding sides are not in the same ratio.

Fig. 6.6
So, the two quadrilaterals are not similar. Similarly, you may note that in the two quadrilaterals (a square and a rhombus) of Fig. 6.7, corresponding sides are in the same ratio, but their corresponding angles are not equal. Again, the two polygons (quadrilaterals) are not similar.

Fig. 6.7
Thus, either of the above two conditions (i) and (ii) of similarity of two polygons is not sufficient for them to be similar.
EXERCISE 6.1
1. Fill in the blanks using the correct word given in brackets :
(i) All circles are ________. (congruent, similar)
(ii) All squares are ________. (similar, congruent)
(iii) All ________ triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are ________ and (b) their corresponding sides are ________.(equal, proportional)
Show Answer
Solution
(i) Similar
(ii) Similar
(iii) Equilateral
(iv) (a) Equal
(b) Proportional
2. Give two different examples of pair of
(i) similar figures.
(ii) non-similar figures.
Show Answer
Solution
(i) Two equilateral triangles with sides

Two squares with sides

(ii) Trapezium and square

Triangle and parallelogram

3. State whether the following quadrilaterals are similar or not:

Fig. 6.8
Show Answer
Solution
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional, i.e. 1:2, but their corresponding angles are not equal.
6.3 Similarity of Triangles
What can you say about the similarity of two triangles?
You may recall that triangle is also a polygon. So, we can state the same conditions for the similarity of two triangles. That is:
Two triangles are similiar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).
Note that if corresponding angles of two triangles are equal, then they are known as equiangular triangles. A famous Greek mathematician Thales gave an important truth relating to two equiangular triangles which is as follows:
The ratio of any two corresponding sides in two equiangular triangles is always the same.
It is believed that he had used a result called the Basic Proportionality Theorem (now known as the Thales Theorem) for the same.

To understand the Basic Proportionality Theorem, let us perform the following activity:
Activity 2 : Draw any angle XAY and on its one arm AX, mark points (say five points) P, Q, D, R and
such that .
Now, through B, draw any line intersecting arm

Fig. 6.9
Also, through the point
Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Proof : We are given a triangle

Fig. 6.10
We need to prove that
Let us join
Now, area of
Recall from Class IX, that area of
Therefore,
and
Note that
Therefore, from (1), (2) and (3), we have :
Is the converse of this theorem also true (For the meaning of converse, see Appendix 1)? To examine this, let us perform the following activity:
Activity 3 : Draw an angle XAY on your notebook and on ray
, mark points , and such that .
Similarly, on ray AY, mark points

Fig. 6.11
Note that
You can also see that lines
Similarly, by joining
From (1), (2), (3) and (4), it can be observed that if a line divides two sides of a triangle in the same ratio, then the line is parallel to the third side.
You can repeat this activity by drawing any angle XAY of different measure and taking any number of equal parts on arms AX and AY. Each time, you will arrive at the same result. Thus, we obtain the following theorem, which is the converse of Theorem 6.1:
Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
This theorem can be proved by taking a line

Fig. 6.12
If
Adding 1 to both sides of above, you can see that
Let us take some examples to illustrate the use of the above theorems.
Example 1 : If a line intersects sides

Fig. 6.13
Solution :
So,
or,
or,
or,
or,
So,
Example 2 : ABCD is a trapezium with

Fig. 6.14
Solution : Let us join AC to intersect

Fig. 6.15
So,
Now, in
EG
So,
Similarly, from
Therefore, from (1) and (2),
Example 3 : In Fig. 6.16,

Fig. 6.16
Solution : It is given that
(Theorem 6.2)
Also, it is given that
Therefore,
i.e.,
EXERCISE 6.2
1. In Fig. 6.17, (i) and (ii),

Fig. 6.17
Show Answer
Solution
(i)

Let
It is given that
By using basic proportionality theorem, we obtain
(ii)

Let
It is given that DE || BC.
By using basic proportionality theorem, we obtain
2.
(i)
(ii)
(iii)
Show Answer
Solution
(i)

Given that,
Hence,
Therefore, EF is not parallel to QR.
(ii)

Hence,
Therefore,
(iii)

Hence,
Therefore, EF is parallel to QR.
3. In Fig. 6.18, if

Fig. 6.18
Show Answer
Solution

In the given figure,
By using basic proportionality theorem, we obtain
Similarly,
From
4. In Fig. 6.19,

Fig. 6.19
Show Answer
Solution

In

In
(ii)
From
5. In Fig. 6.20, DE

Fig. 6.20
Show Answer
Solution

In
(i)

In
From

6. In Fig. 6.21, A, B and

Fig. 6.21
Show Answer
Solution

In
(i)

In
From

7. Using Theorem 6.1 , prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Show Answer
Solution

Consider the given figure in which
By using basic proportionality theorem, we obtain
Or,
8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Show Answer
Solution

Consider the given figure in which
i.e.,
It can be observed that
and
Hence, by using basic proportionality theorem, we obtain
9.
Show Answer
Solution

Draw a line
In
By using basic proportionality theorem, we obtain
In
So, by using basic proportionality theorem, we obtain
From equations (1) and (2), we obtain
10. The diagonals of a quadrilateral
Show Answer
Solution
Let us consider the following figure for the given question.

Draw a line

In
By using basic proportionality theorem, we obtain
However, it is given that
From equations (1) and (2), we obtain
6.4 Criteria for Similarity of Triangles
In the previous section, we stated that two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
That is, in
(i)
(ii)

Fig. 6.22
Here, you can see that A corresponds to D, B corresponds to E and C corresponds to F. Symbolically, we write the similarity of these two triangles as ’
It must be noted that as done in the case of congruency of two triangles, the similarity of two triangles should also be expressed symbolically, using correct correspondence of their vertices. For example, for the triangles
Now a natural question arises : For checking the similarity of two triangles, say
Activity 4 : Draw two line segments
and of two different lengths, say 3 cm and 5 cm respectively. Then, at the points and respectively, construct angles and QCB of some measures, say, and . Also, at the points and , construct angles REF and SFE of and respectively (see Fig. 6.23).

Fig. 6.23
Let rays
Theorem 6.3 : If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
This criterion is referred to as the AAA (Angle-Angle-Angle) criterion of similarity of two triangles.
This theorem can be proved by taking two triangles

Fig. 6.24
Cut
Similarly,
Remark : If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal. Therefore, AAA similarity criterion can also be stated as follows:
If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
This may be referred to as the AA similarity criterion for two triangles.
You have seen above that if the three angles of one triangle are respectively equal to the three angles of another triangle, then their corresponding sides are proportional (i.e., in the same ratio). What about the converse of this statement? Is the converse true? In other words, if the sides of a triangle are respectively proportional to the sides of another triangle, is it true that their corresponding angles are equal? Let us examine it through an activity :
Activity 5 : Draw two triangles
and such that AB = 3 cm, BC = 6 cm, CA = 8 cm, DE = 4.5 cm, EF = 9 cm and FD = 12 cm (see Fig. 6.25).

Fig. 6.25
So, you have :
Now measure
You can repeat this activity by drawing several such triangles (having their sides in the same ratio). Everytime you shall see that their corresponding angles are equal. It is due to the following criterion of similarity of two triangles:
Theorem 6.4 : If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar.
This criterion is referred to as the SSS (Side-Side-Side) similarity criterion for two triangles.
This theorem can be proved by taking two triangles

Fig. 6.26
Cut
It can be seen that
Remark : You may recall that either of the two conditions namely, (i) corresponding angles are equal and (ii) corresponding sides are in the same ratio is not sufficient for two polygons to be similar. However, on the basis of Theorems 6.3 and 6.4, you can now say that in case of similarity of the two triangles, it is not necessary to check both the conditions as one condition implies the other.
Let us now recall the various criteria for congruency of two triangles learnt in Class IX. You may observe that SSS similarity criterion can be compared with the SSS congruency criterion. This suggests us to look for a similarity criterion comparable to SAS congruency criterion of triangles. For this, let us perform an activity.
Activity 6 : Draw two triangles
and such that , and (see Fig.6.27).

Fig. 6.27
Here, you may observe that
You will find that
Theorem 6.5: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
This criterion is referred to as the SAS (Side-Angle-Side) similarity criterion for two triangles.
As before, this theorem can be proved by taking two triangles

Fig. 6.28
We now take some examples to illustrate the use of these criteria.
Example 4 : In Fig. 6.29, if PQ

Fig. 6.29
Solution :
Example 5 : Observe Fig. 6.30 and then find

Fig. 6.30
Solution : In
That is,
So,
Therefore,
But
So,
Example 6 : In Fig. 6.31,

Show that
Solution:
So,
Also, we have
Therefore, from (1) and (2),
So,
Example 7 : A girl of height
Solution : Let AB denote the lamp-post and CD the girl after walking for 4 seconds away from the lamp-post (see Fig. 6.32).

Fig. 6.32
From the figure, you can see that DE is the shadow of the girl. Let
Now,
Note that in
So, the shadow of the girl after walking for 4 seconds is 1.6 m long.
Example 8 : In Fig. 6.33,

Fig. 6.33
(i)
(ii)
(iii)
Solution : (i)
So,
and
But
So, from (1),
i.e.,
Also,
So, from (3) and (4),
(ii) From (5),
But
Therefore,
(iii) Again,
Therefore
Also,
i.e.,
i.e.,
Therefore,
[Note : You can also prove part (iii) by following the same method as used for proving part (i).]
EXERCISE 6.3
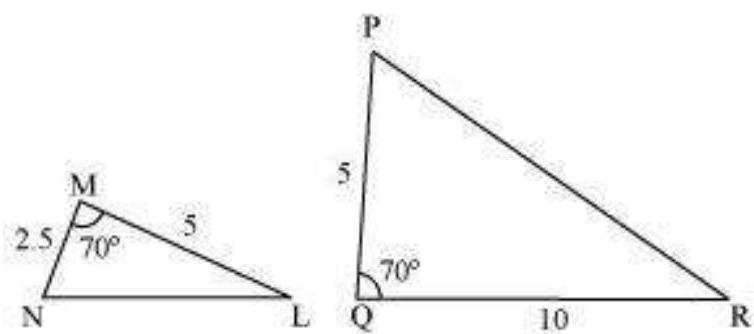
1. State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Show Answer
Solution
(i)
Therefore,
(ii)
[By SSS similarity criterion]
(iii)The given triangles are not similar as the corresponding sides are not proportional.
2. In Fig. 6.35,
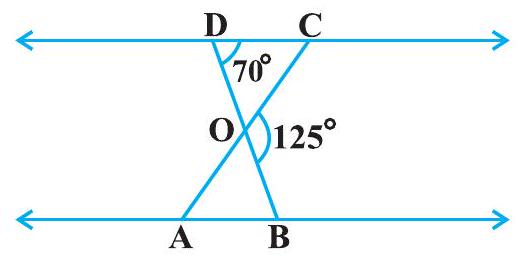
Fig. 6.35
Show Answer
Solution
DOB is a straight line.
In
(Sum of the measures of the angles of a triangle is
It is given that
3. Diagonals
Show Answer
#missing4. In Fig. 6.36,
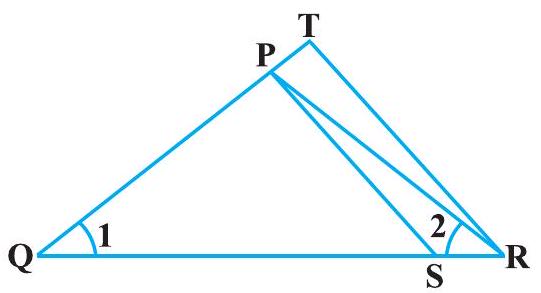
Fig. 6.36
Show Answer
Solution
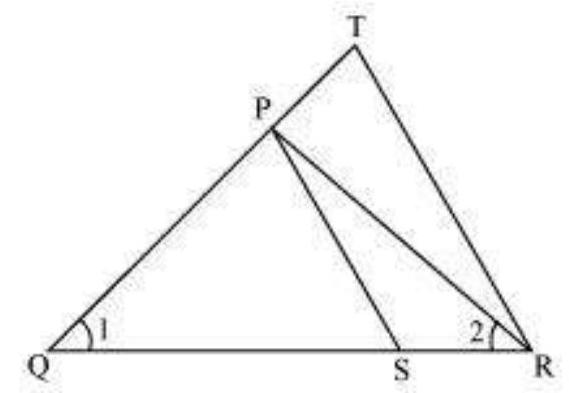
In
Given,
Using
In
5.
Show Answer
Solution
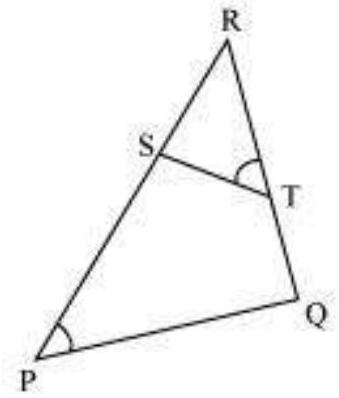
In
6. In Fig. 6.37, if
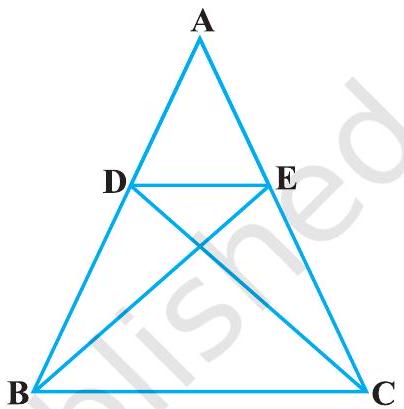
Fig. 6.37
Show Answer
Solution
It is given that
And,
In
[Dividing equation (2) by (1)]
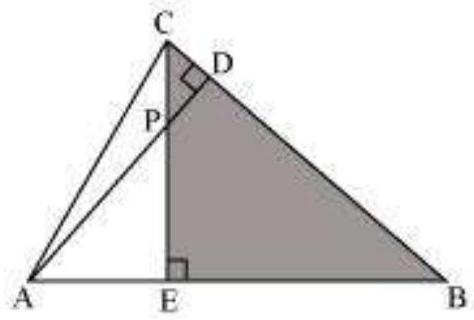
7. In Fig. 6.38, altitudes
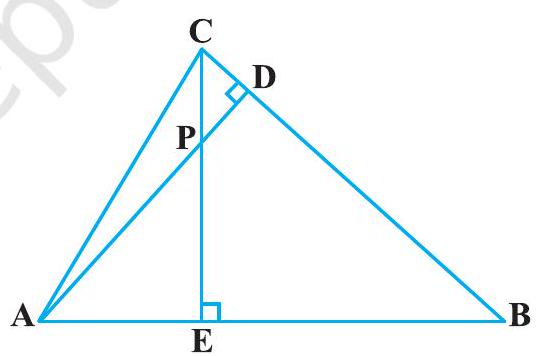
Fig. 6.38
(i)
(ii)
(iii)
(iv)
Show Answer
Solution
(i)
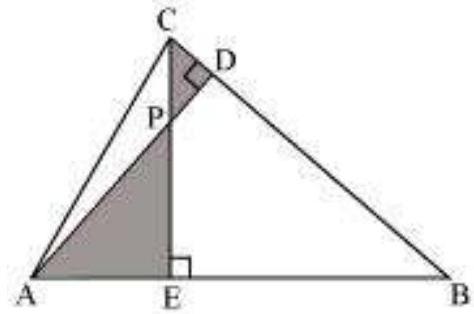
In
Hence, by using AA similarity criterion,
(ii)
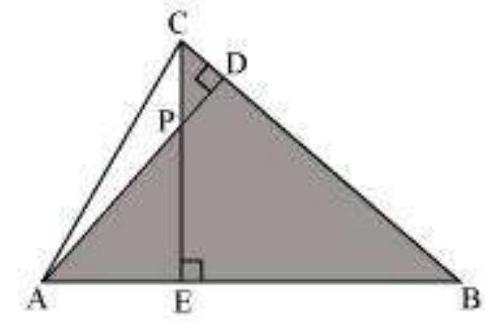
In
Hence, by using AA similarity criterion,
(iii)
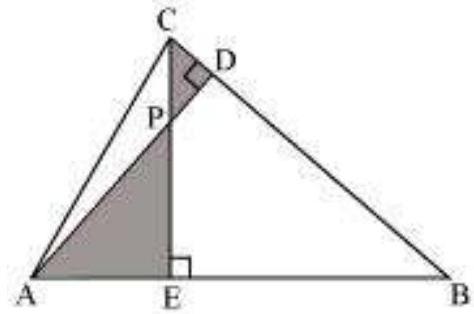
In
Hence, by using AA similarity criterion,
(iv)
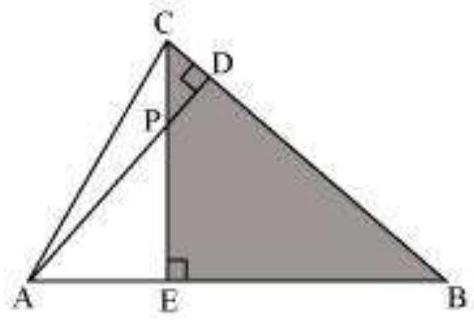
In
Hence, by using AA similarity criterion,
8.
Show Answer
Solution
In
9. In Fig. 6.39,
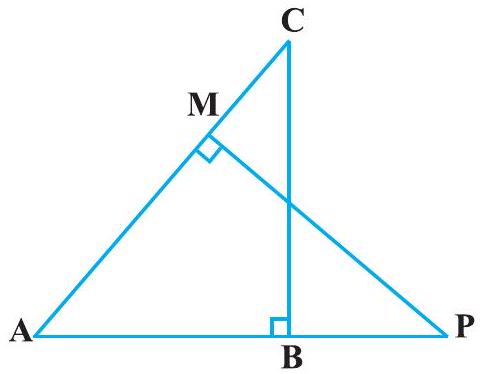
Fig. 6.39
(i)
(ii)
Show Answer
Solution
In
10.
(i)
(ii)
(iii)
Show Answer
Solution
Answer :

It is given that
And,
In
In
In
11. In Fig. 6.40,
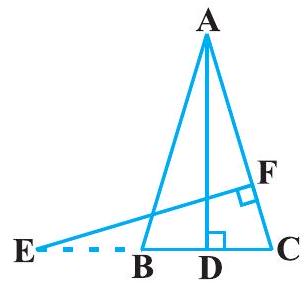
Fig. 6.40
Show Answer
Solution
It is given that
In
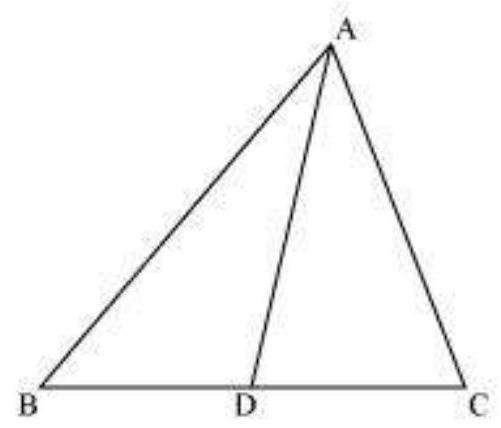
12. Sides
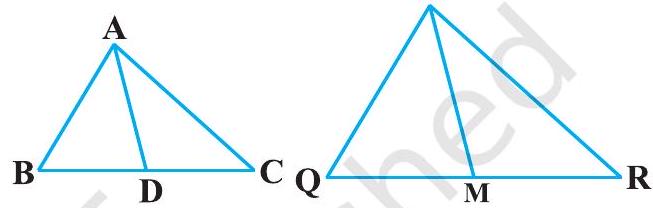
Fig. 6.41
Show Answer
Solution
Median divides the opposite side.
Given that,
In
In
13.
Show Answer
Solution
In
We know that corresponding sides of similar triangles are in proportion.
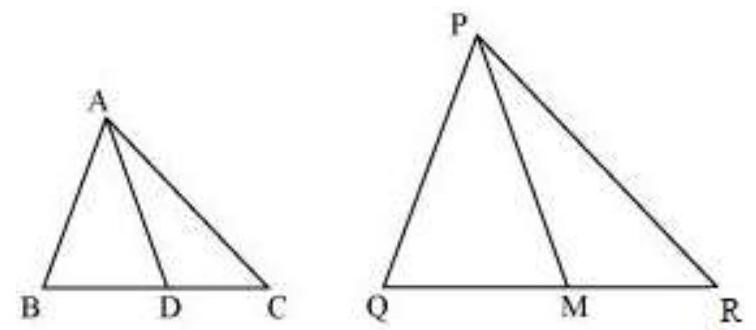
14. Sides
Show Answer
Solution
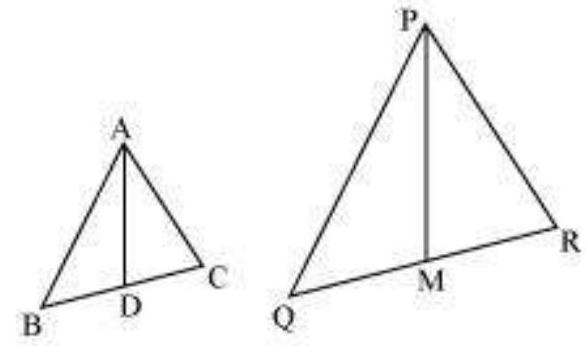
Given that,
Let us extend 
We know that medians divide opposite sides.
Therefore,
Also,
And,
In quadrilateral
Therefore, quadrilateral ABEC is a parallelogram.
Similarly, we can prove that quadrilateral
It was given that
We know that corresponding angles of similar triangles are equal.
Similarly, it can be proved that
Adding equation (1) and (2), we obtain
In
(Given)
15. A vertical pole of length
Show Answer
Solution
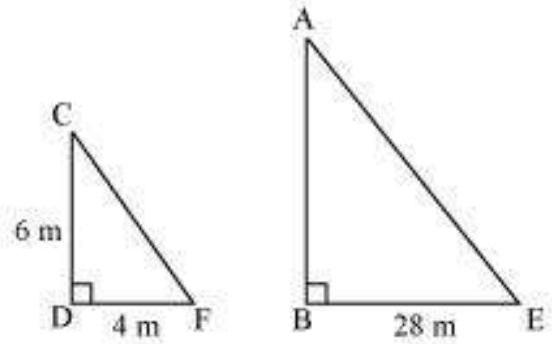
Let
Let the shadow of
At the same time, the light rays from the sun will fall on the tower and the pole at the same angle.
Therefore,
And,
Therefore, the height of the tower will be 42 metres.
16. If
Show Answer
Solution
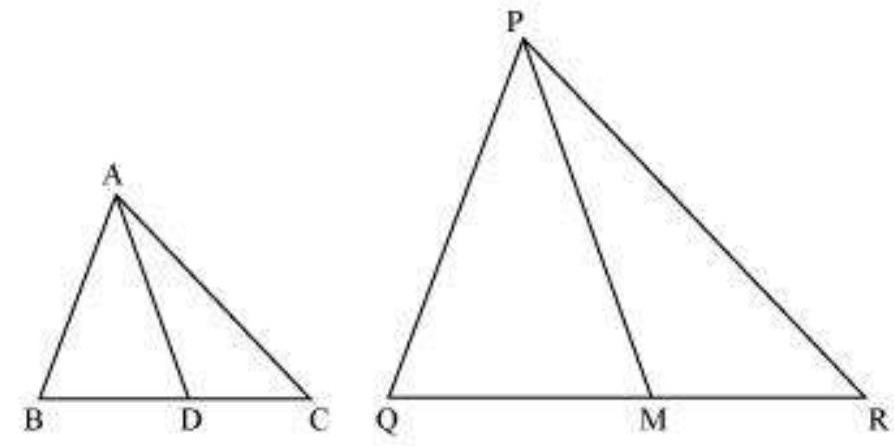
It is given that
We know that the corresponding sides of similar triangles are in proportion.
Also,
Since AD and PM are medians, they will divide their opposite sides.
From equations ( 1 ) and (3), we obtain
In
6.5 Summary
In this chapter you have studied the following points :
1. Two figures having the same shape but not necessarily the same size are called similar figures.
2. All the congruent figures are similar but the converse is not true.
3. Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (i.e., proportion).
4. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
5. If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
6. If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar (AAA similarity criterion).
7. If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar (AA similarity criterion).
8. If in two triangles, corresponding sides are in the same ratio, then their corresponding angles are equal and hence the triangles are similar (SSS similarity criterion).
9. If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are similar (SAS similarity criterion).
A NOTE TO THE READER
If in two right triangles, hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of the other triangle, then the two triangles are similar. This may be referred to as the RHS Similarity Criterion.
If you use this criterion in Example 2 , Chapter 8, the proof will become simpler.










