अध्याय 06 त्रिभुज
6.1 भूमिका
आप अपनी पिछली कक्षाओं से, त्रिभुजों और उनके अनेक गुणधर्मों से भली भाँति परिचित हैं। कक्षा IX में, आप त्रिभुजों की सर्वांगसमता के बारे में विस्तृत रूप से अध्ययन कर चुके हैं। याद कीजिए कि दो त्रिभुज सर्वांगसम तब कहे जाते हैं जब उनके समान आकार (shape) तथा समान आमाप (size) हों। इस अध्याय में, हम ऐसी आकृतियों के बारे में अध्ययन करेंगे जिनके आकार समान हों परंतु उनके आमाप का समान होना आवश्यक नहीं हो। दो आकृतियाँ जिनके समान आकार हों (परंतु समान आमाप होना आवश्यक न हो) समरूप आकृतियाँ (similar figures) कहलाती हैं। विशेष रूप से, हम समरूप त्रिभुजों की चर्चा करेंगे तथा इस जानकारी को पहले पढ़ी गई पाइथागोरस प्रमेय की एक सरल उपपत्ति देने में प्रयोग करेंगे।

क्या आप अनुमान लगा सकते हैं कि पर्वतों (जैसे माऊंट एवरेस्ट) की ऊँचाईयाँ अथवा कुछ दूरस्थ वस्तुओं (जैसे चन्द्रमा) की दूरियाँ किस प्रकार ज्ञात की गई हैं? क्या आप सोचते हैं कि इन्हें एक मापने वाले फीते से सीधा (प्रत्यक्ष) मापा गया है? वास्तव में, इन सभी ऊँचाई और दूरियों को अप्रत्यक्ष मापन (indirect measurement) की अवधारणा का प्रयोग करते हुए ज्ञात किया गया है, जो आकृतियों की समरूपता के सिद्धांत पर आधारित है (देखिए उदाहरण 7 , प्रश्नावली 6.3 का प्रश्न 15 तथा साथ ही इस पुस्तक के अध्याय 8 और 9)।
6.2 समरूप आकृतियाँ
कक्षा IX में, आपने देखा था कि समान (एक ही) त्रिज्या वाले सभी वृत्त सर्वांगसम होते हैं, समान लंबाई की भुजा वाले सभी वर्ग सर्वांगसम होते हैं तथा समान लंबाई की भुजा वाले सभी समबाहु त्रिभुज सर्वांगसम होते हैं।

आकृति 6.1
अब किन्हीं दो (या अधिक) वृत्तों पर विचार कीजिए [देखिए आकृति 6.1 (i)]। क्या ये सर्वांगसम हैं? चूँकि इनमें से सभी की त्रिज्या समान नहीं है, इसलिए ये परस्पर सर्वांगसम नहीं हैं। ध्यान दीजिए कि इनमें कुछ सर्वांगसम हैं और कुछ सर्वांगसम नहीं हैं, परंतु इनमें से सभी के आकार समान हैं। अतः, ये सभी वे आकृतियाँ हैं जिन्हें हम समरूप (similar) कहते हैं। दो समरूप आकृतियों के आकार समान होते हैं परंतु इनके आमाप समान होने आवश्यक नहीं हैं। अतः, सभी वृत्त समरूप होते हैं। दो (या अधिक) वर्गों के बारे में अथवा दो (या अधिक) समबाहु त्रिभुजों के बारे में आप क्या सोचते हैं [देखिए आकृति 6.1 (ii) और (iii)]? सभी वृत्तों की तरह ही, यहाँ सभी वर्ग समरूप हैं तथा सभी समबाहु त्रिभुज समरूप हैं।
उपरोक्त चर्चा से, हम यह भी कह सकते हैं कि सभी सर्वांगसम आकृतियाँ समरूप होती हैं, परंतु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
क्या एक वृत्त और एक वर्ग समरूप हो सकते हैं? क्या एक त्रिभुज और एक वर्ग समरूप हो सकते हैं? इन आकृतियों को देखने मात्र से ही आप प्रश्नों के उत्तर दे सकते हैं (देखिए आकृति 6.1)। स्पष्ट शब्दों में, ये आकृतियाँ समरूप नहीं हैं। (क्यों?)

आकृति 6.2
आप दो चतुर्भुजों

आकृति 6.3
आप तुरंत यह कहेंगे कि ये एक ही स्मारक (ताजमहल) के चित्र हैं, परंतु ये भिन्न-भिन्न आमापों (sizes) के हैं। क्या आप यह कहेंगे कि ये चित्र समरूप हैं? हाँ, ये हैं।
आप एक ही व्यक्ति के एक ही आमाप वाले उन दो चित्रों के बारे में क्या कह सकते हैं, जिनमें से एक उसकी 10 वर्ष की आयु का है तथा दूसरा उसकी 40 वर्ष की आयु का है? क्या ये दोनों चित्र समरूप हैं? ये चित्र समान आमाप के हैं, परंतु निश्चित रूप से ये समान आकार के नहीं हैं। अतः, ये समरूप नहीं हैं।
जब कोई फ़ोटोग्राफर एक ही नेगेटिव से विभिन्न मापों के फ़ोटो प्रिंट निकालती है, तो वह क्या करती है? आपने स्टैंप साइज़, पासपोर्ट साइज़ एवं पोस्ट कार्ड साइज़ फ़ोटो (या चित्रों) के बारे में अवश्य सुना होगा। वह सामान्य रूप से एक छोटे आमाप (साइज) की फ़िल्म (film), मान लीजिए जो
भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि
ध्यान दीजिए कि बहुभुजों के लिए संगत भुजाओं के इस एक ही अनुपात को स्केल गुणक (scale factor) [अथवा प्रतिनिधित्व भिन्न (Representative Fraction)] कहा जाता है। आपने यह अवश्य सुना होगा कि विश्व मानचित्र [अर्थात् ग्लोबल मानचित्र] तथा भवनों के निर्माण के लिए बनाए जाने वाली रूप रेखा एक उपयुक्त स्केल गुणक तथा कुछ परिपाटियों को ध्यान में रखकर बनाए जाते हैं।
आकृतियों की समरूपता को अधिक स्पष्ट रूप से समझने के लिए, आइए निम्नलिखित क्रियाकलाप करें:
क्रियाकलाप 1 : अपनी कक्षा के कमरे की छत के किसी बिंदु
ध्यान दीजिए कि चतुर्भुज

आकृति 6.4
अतः चतुर्भुज
यहाँ, आप यह भी देख सकते हैं कि शीर्ष
(i)
(ii)
इससे पुनः यह बात स्पष्ट होती है कि भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि
उपरोक्त के आधार पर, आप सरलता से यह कह सकते हैं कि आकृति 6.5 में दिए गए चतुर्भुज

आकृति 6.5
टिप्पणी: आप इसका सत्यापन कर सकते हैं कि यदि एक बहुभुज किसी अन्य बहुभुज के समरूप हो और यह दूसरा बहुभुज एक तीसरे बहुभुज के समरूप हो, तो पहला बहुभुज तीसरे बहुभुज के समरूप होगा।
आप यह देख सकते हैं कि आकृति 6.6 के दो चतुर्भुजों (एक वर्ग और एक आयत) में, संगत कोण बराबर हैं, परंतु इनकी संगत भुजाएँ एक ही अनुपात में नहीं हैं। अतः, ये दोनों चतुर्भुज समरूप नहीं हैं।

आकृति 6.6
इसी प्रकार आप देख सकते हैं कि आकृति 6.7 के दो चतुर्भुजों (एक वर्ग और एक समचतुर्भुज) में, संगत भुजाएँ एक ही अनुपात में हैं, परंतु इनके संगत कोण बराबर नहीं हैं। पुनः, दोनों बहुभुज (चतुर्भुज) समरूप नहीं हैं।

आकृति 6.7
इस प्रकार, आप देख सकते हैं कि दो बहुभुजों की समरूपता के प्रतिबंधों (i) और (ii) में से किसी एक का ही संतुष्ट होना उनकी समरूपता के लिए पर्याप्त नहीं है।
प्रश्नावली 6.1
1. कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए:
(i) सभी वृत्त __________ होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग ________ होते हैं। (समरूप, सर्वांगसम)
(iii) सभी ________ त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण ______ हों तथा (ii) उनकी संगत भुजाएँ _______ हों। (बराबर, समानुपाती)
Show Answer
#missing2. निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।
Show Answer
#missing3. बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:

आकृति 6.8
Show Answer
#missing6.3 त्रिभुजों की समरूपता
आप दो त्रिभुजों की समरूपता के बारे में क्या कह सकते हैं?
आपको याद होगा कि त्रिभुज भी एक बहुभुज ही है। इसलिए, हम त्रिभुजों की समरूपता के लिए भी वही प्रतिबंध लिख सकते हैं, जो बहुभुजों की समरूपता के लिए लिखे थे। अर्थात्
दो त्रिभुज समरूप होते हैं, यदि
(i) उनके संगत कोण बराबर हों तथा
(ii) उनकी संगत भुजाएँ एक ही अनुपात में (अर्थात् समानुपाती) हों।
ध्यान दीजिए कि यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे समानकोणिक त्रिभुज (equiangular triangles) कहलाते हैं। एक प्रसिद्ध यूनानी गणितज्ञ थेल्स (Thales) ने दो समानकोणिक त्रिभुजों से संबंधित एक महत्वपूर्ण तथ्य प्रतिपादित किया, जो नीचे दिया जा रहा है:
दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है।
ऐसा विश्वास किया जाता है कि इसके लिए उन्होंने एक परिणाम का प्रयोग किया जिसे आधारभूत समानुपातिकता प्रमेय (आजकल थेल्स प्रमेय) कहा जाता है।

आधारभूत समानुपातिकता प्रमेय (Basic Proportionality Theorem) को समझने के लिए, आइए निम्नलिखित क्रियाकलाप करें:
क्रियाकलाप 2 : कोई कोण XAY खींचिए तथा उसकी एक भुजा
अब, बिंदु

आकृति 6.9
साथ ही, बिंदु
प्रमेय 6.1: यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
उपपत्ति : हमें एक त्रिभुज

आकृति 6.10
हमें सिद्ध करना है कि
आवृति 6.10 आइए
अब,
कक्षा IX से याद कीजिए कि
अत:
इसी प्रकार
अत :
तथा
ध्यान दीजिए कि
अत:
इसलिए (1), (2) और (3), से हमें प्राप्त होता है:
क्या इस प्रमेय का विलोम भी सत्य है (विलोम के अर्थ के लिए परिशिष्ट 1 देखिए)? इसकी जाँच करने के लिए, आइए निम्नलिखित क्रियाकलाप करें:
क्रियाकलाप 3 : अपनी अभ्यासपुस्तिका में एक कोण
इसी प्रकार, किरण

आकृति 6.11
ध्यान दीजिए कि
आप यह भी देख सकते हैं कि रेखाएँ
इसी प्रकार, क्रमशः
(1), (2), (3) और (4) से, यह देखा जा सकता है कि यदि कोई रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह रेखा तीसरी भुजा के समांतर होती हैं।
आप किसी अन्य माप का कोण XAY खींचकर तथा भुजाओं
प्रमेय 6.2 : यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो वह तीसरी भुजा के समांतर होती है।
इस प्रमेय को सिद्ध किया जा सकता है, यदि हम एक रेखा

आकृति 6.12
अब यदि
अत:
इसलिए
उपरोक्त के दोनों पक्षों में 1 जोड़ कर, आप यह देख सकते हैं कि
उपरोक्त प्रमेयों का प्रयोग स्पष्ट करने के लिए आइए कुछ उदाहरण लें।
उदाहरण 1 : यदि कोई रेखा एक

आकृति 6.13
हल :
अत:
या
या
या
या
अत:
उदाहरण 2 :

आकृति 6.14
हल : आइए

आकृति 6.15
इसलिए
अब
EG || DC (क्योंकि EF || DC)
अत:
इसी प्रकार,
अर्थात्
अतः (1) और (2) से
उदाहरण 3 : आकृति 6.16 में

आकृति 6.16
हल : यह दिया है कि,
अत:
(प्रमेय 6.2 )
इसलिए
साथ ही यह दिया है कि
अत :
इसलिए
अर्थात्
प्रश्नावली 6.2
1. आकृति 6.17 (i) और (ii) में,

आकृति 6.17
Show Answer
#missing2. किसी
(i)
(ii)
(iii)
Show Answer
#missing3. आकृति 6.18 में यदि

आकृति 6.18
Show Answer
#missing4. आकृति 6.19 में

आकृति 6.19
Show Answer
#missing5. आकृति 6.20 में

आकृति 6.20
Show Answer
#missing6. आकृति 6.21 में क्रमश:

आकृति 6.21
Show Answer
#missing7. प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
Show Answer
#missing8. प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
Show Answer
#missing9.
Show Answer
#missing10. एक चतुर्भुज
Show Answer
#missing6.4 त्रिभुजों की समरूपता के लिए कसौटियाँ
पिछले अनुच्छेद में हमने कहा था कि दो त्रिभुज समरूप होते हैं यदि (i) उनके संगत कोण बराबर हों तथा (ii) उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती हों)। अर्थात्
यदि
(i)
(ii)

आकृति 6.22
यहाँ आप देख सकते हैं कि
इस बात पर अवश्य ध्यान देना चाहिए कि जैसा त्रिभुजों की सर्वांगसमता की स्थिति में किया गया था त्रिभुजों की समरूपता को भी सांकेतिक रूप से व्यक्त करने के लिए, उनके शीर्षों की संगतताओं को सही क्रम में लिखा जाना चाहिए। उदाहरणार्थ, आकृति 6.22 के त्रिभुजों
अब एक प्रश्न यह उठता है: दो त्रिभुजों, मान लीजिए
क्रियाकलाप 4 : भिन्न-भिन्न लंबाइयों, मान लीजिए

आकृति 6.23
मान लीजिए किरण
प्रमेय 6.3 : यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं।
उपरोक्त कसौटी को दो त्रिभुजों की समरूपता कीAAA ( कोण-कोण-कोण) कसौटी कहा जाता है।
इस प्रमेय को दो ऐसे त्रिभुज

आकृति 6.24
अत:
इससे
अत :
अर्थात्
इसी प्रकार,
टिप्पणी: यदि एक त्रिभुज के दो कोण किसी अन्य त्रिभुज के दो कोणों के क्रमशः बराबर हों, तो त्रिभुज के कोण योग गुणधर्म के कारण, इनके तीसरे कोण भी बराबर होंगे। इसीलिए, AAA समरूपता कसौटी को निम्नलिखित रूप में भी व्यक्त किया जा सकता है:
यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमशः दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं।
उपरोक्त को दो त्रिभुजों की समरूपता की
ऊपर आपने देखा है कि यदि एक त्रिभुज के तीनों कोण क्रमशः दूसरे त्रिभुज के तीनों कोणों के बराबर हों, तो उनकी संगत भुजाएँ समानुपाती (एक ही अनुपात में) होती हैं। इस कथन के विलोम के बारे में क्या कह सकते हैं? क्या यह विलोम सत्य है? दूसरे शब्दों में, यदि एक त्रिभुज की भुजाएँ क्रमशः दूसरे त्रिभुज की भुजाओं के समानुपाती हों, तो क्या यह सत्य है कि इन त्रिभुजों के संगत कोण बराबर हैं? आइए, एक क्रियाकलाप द्वारा जाँच करें।
क्रियाकलाप 5 : दो त्रिभुज

आकृति 6.25
तब, आपको प्राप्त है:
अब,
इसी प्रकार के अनेक त्रिभुजों के युग्म खींचकर (जिनमें संगत भुजाओं के अनुपात एक ही हों), आप इस क्रियाकलाप को पुनः कर सकते हैं। प्रत्येक बार आप यह पाएँगे कि इन त्रिभुजों के संगत कोण बराबर हैं। यह दो त्रिभुजों की समरूपता की निम्नलिखित कसौटी के कारण हैं:
प्रमेय 6.4 : यदि दो त्रिभुजों में एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती (अर्थात् एक ही अनुपात में) हों, तो इनके संगत कोण बराबर होते हैं, और इसीलिए दोनों त्रिभुज समरूप होते हैं।
इस कसौटी को दो त्रिभुजों की समरूपता की
उपरोक्त प्रमेय को ऐसे दो त्रिभुज

आकृति 6.26
यहाँ यह देखा जा सकता है कि
अत:
इसलिए
जिससे
अत:
इस प्रकार
अतः
टिप्पणी: आपको याद होगा कि दो बहुभुजों की समरूपता के दोनों प्रतिबंधों, अर्थात् (i) संगत कोण बराबर हों और (ii) संगत भुजाएँ एक ही अनुपात में हों, में से केवल किसी एक का ही संतुष्ट होना उनकी समरूपता के लिए पर्याप्त नहीं होता। परंतु प्रमेयों 6.3 और 6.4 के आधार पर, अब आप यह कह सकते हैं कि दो त्रिभुजों की समरूपता की स्थिति में, इन दोनों प्रतिबंधों की जाँच करने की आवश्यकता नहीं है, क्योंकि एक प्रतिबंध से स्वतः ही दूसरा प्रतिबंध प्राप्त हो जाता है।
आइए अब दो त्रिभुजों की सर्वांगसमता की उन कसौटियों को याद करें, जो हमने कक्षा IX में पढ़ी थीं। आप देख सकते हैं कि SSS समरूपता कसौटी की तुलना SSS सर्वांगसमता कसौटी से की जा सकती है। इससे हमें यह संकेत मिलता है कि त्रिभुजों की समरूपता की ऐसी कसौटी प्राप्त करने का प्रयत्न किया जाए जिसकी त्रिभुजों की SAS सर्वांगसमता कसौटी से तुलना की जा सके। इसके लिए, आइए एक क्रियाकलाप करें।
क्रियाकलाप 6 : दो त्रिभुज

आकृति 6.27
यहाँ, आप देख सकते हैं कि
आप पाएँगे कि
प्रमेय 6.5: यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ समानुपाती हों, तो दोनों त्रिभुज समरूप होते हैं।
इस कसौटी को दो त्रिभुजों की समरूपता की
पहले की ही तरह, इस प्रमेय को भी दो त्रिभुज

आकृति 6.28
अब
अतः
इसलिए
आइए अब हम इन कसौटियों के प्रयोग को प्रदर्शित करने के लिए, कुछ उदाहरण लें।
उदाहरण 4 : आकृति 6.29 में, यदि

आकृति 6.29
हल :
अत :
और
साथ ही
इसलिए
उदाहरण 5 : आकृति 6.30 में

आकृति 6.30
हल :
अर्थात्
इसलिए
इसलिए
परंतु
अत :
उदाहरण 6 : आकृति 6.31 में,

दर्शाइए कि
हल ::
So,
साथ ही, हमें प्राप्त हैं :
(SAS समरूपता कसौटी)
अतः (1) और (2) से
इसलिए
उदाहरण 7:
हल : मान लीजिए

आकृति 6.32
आकृति से आप देख सकते हैं कि
अब,
ध्यान दीजिए कि
अतः 4 सेकंड चलने के बाद लड़की की छाया की लंबाई
उदाहरण 8 : आकृति 6.33 में

आकृति 6.33
(i)
(ii)
(iii)
हल : (i)
So,
और
लेकिन
इसलिए (1) से ,
अथार्थ
साथ ही
इसलिए, (3) और (4) से
(ii) (5) से,
लेकिन
इसलिए
(iii) पुनः
इसलिए
साथ ही
अथार्थ
अथार्थ
इसलिए
[टिप्पणी: आप इस प्रश्न के भाग (iii) को भाग (i) में प्रयोग की गई विधि से भी सिद्ध कर सकते हैं।]
प्रश्नावली 6.3
1. बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।

Show Answer
#missing2. आकृति 6.35 में,
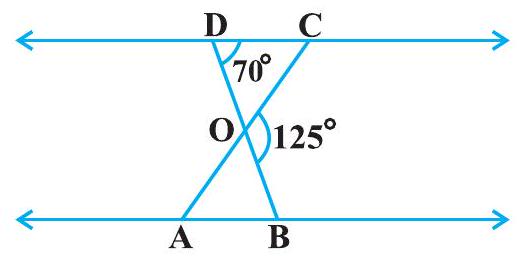
आकृति 6.35
Show Answer
#missing3. समलंब
Show Answer
#missing4. आकृति 6.36 में,
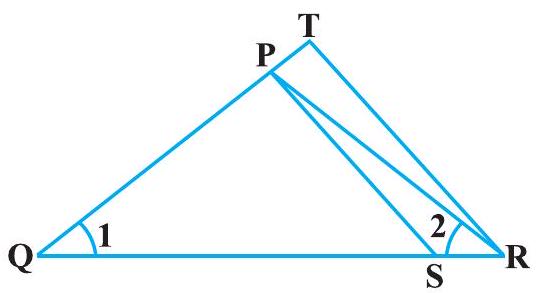
आकृति 6.36
Show Answer
#missing5.
Show Answer
#missing6. आकृति 6.37 में, यदि
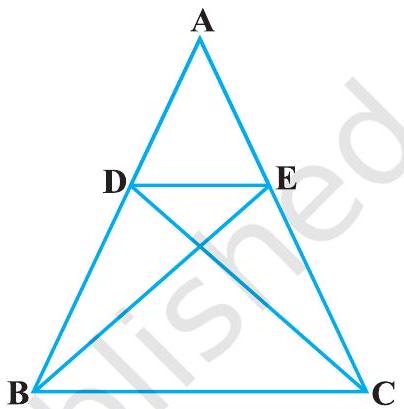
आकृति 6.36
Show Answer
#missing7. आकृति 6.38 में,
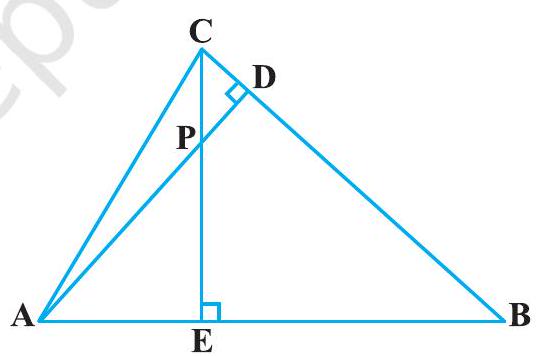
आवृति 6.38
(i)
(ii)
(iii)
(iv)
Show Answer
#missing- समांतर चतुर्भुज
Show Answer
#missing- आकृति 6.39 में,
आकृति 6.39
(i)
(ii)
Show Answer
#missing
(i)
(ii)
(iii)
Show Answer
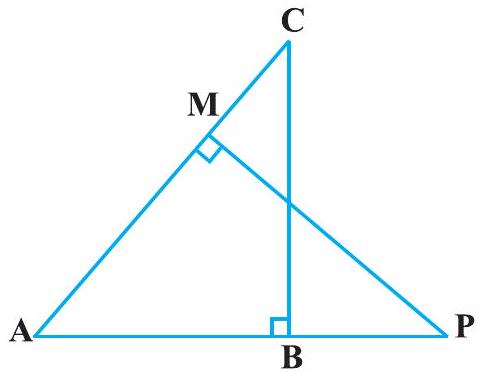
#missing11. आकृति 6.40 में,
आवृत्ति 6.40
Show Answer
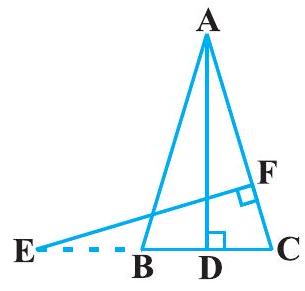
#missing12. एक त्रिभुज
आवृति 6.41
Show Answer
#missing13. एक त्रिभुज
Show Answer
#missing14. एक त्रिभुज
Show Answer
#missing15. लंबाई
Show Answer
#missing16.
Show Answer
#missing6.5 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है:
1. दो आकृतियाँ जिनके आकार समान हों, परंतु आवश्यक रूप से आमाप समान न हों, समरूप आकृतियाँ कहलाती हैं।
2. सभी सर्वांगसम आकृतियाँ समरूप होती हैं परंतु इसका विलोम सत्य नहीं है।
3. भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण बराबर हों तथा (ii) उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) हों।
4. यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए, एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
5. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो यह रेखा तीसरी भुजा के समांतर होती है।
6. यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में होती हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (AAA समरूपता कसौटी)।
7. यदि दो त्रिभुजों में, एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं (AA समरूपता कसौटी)।
8. यदि दो त्रिभुजों में, संगत भुजाएँ एक ही अनुपात में हों, तो उनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (SSS समरूपता कसौटी)।
9. यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों, तो दोनों त्रिभुज समरूप होते हैं(SAS समरूपता कसौटी)।
पाठकों के लिए विशेष
यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण तथा एक भुजा, दूसरे त्रिभुज के कर्ण तथा एक भुजा के समानुपाती हो तो दोनों त्रिभुज समरूप होते हैं। इसे RHS समरूपता कसौटी कहा जा सकता है।
यदि आप इस कसौटी को अध्याय 8 के उदाहरण 2 में प्रयोग करते हैं तो उपपति और भी सरल हो जाएगी।










