10.1 Area of a Triangle — by Heron’s Formula

We know that the area of triangle when its height is given, is $\frac{1}{2}\times$ base $\times$ height. Now suppose that we know the lengths of the sides of a scalene triangle and not the height. Can you still find its area? For instance, you have a triangular park whose sides are 40 $\mathrm{m},32\mathrm{m}$, and $24\mathrm{m}$. How will you calculate its area? Definitely if you want to apply the formula, you will have to calculate its height. But we do not have a clue to calculate the height. Try doing so. If you are not able to get it, then go to the next section.

Heron was born in about 10AD possibly in Alexandria in Egypt. He worked in applied mathematics. His works on mathematical and physical subjects are so numerous and varied that he is considered to be an encyclopedic writer in these fields. His geometrical works deal largely with problems on mensuration written in three books. Book I deals with the area of squares, rectangles, triangles, trapezoids (trapezia), various other specialised quadrilaterals, the regular polygons, circles, surfaces of cylinders, cones, spheres etc. In this book, Heron has derived the famous formula for the area of a triangle in terms of its three sides.

Fig. 10.1

The formula given by Heron about the area of a triangle, is also known as Hero’s formula. It is stated as:

$$\text{ Area of a triangle }=\sqrt{s(s-a)(s-b)(s-c)}$$

where $a,b$ and $c$ are the sides of the triangle, and $s=$ semi-perimeter, i.e., half the perimeter of the triangle $=\frac{a+b+c}{2}$,

This formula is helpful where it is not possible to find the height of the triangle easily. Let us apply it to calculate the area of the triangular park $\mathrm{ABC}$, mentioned above (see Fig. 10.2).

Fig. 10.2

Let us take $a=40\mathrm{m},b=24\mathrm{m},c=32\mathrm{m}$,

so that we have $$s=\frac{40+24+32}{2}\mathrm{m}=48\mathrm{m}$$.

$s-a=(48-40)\mathrm{m}=8\mathrm{m}$,

$s-b=(48-24)\mathrm{m}=24\mathrm{m}$,

$s-c=(48-32)\mathrm{m}=16\mathrm{m}$.

Therefore, area of the park $\mathrm{ABC}$

$=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{48\times 8\times 24\times 16}{\mathrm{m}}^2=384{\mathrm{m}}^2$

We see that ${32}^2+{24}^2=1024+576=1600={40}^2$. Therefore, the sides of the park make a right triangle. The largest side, i.e., $\mathrm{BC}$ which is $40\mathrm{m}$ will be the hypotenuse and the angle between the sides $\mathrm{AB}$ and $\mathrm{AC}$ will be ${90}^{\circ }$.

We can check that the area of the park is $\frac{1}{2}\times 32\times 24{\mathrm{m}}^2=384{\mathrm{m}}^2$.

We find that the area we have got is the same as we found by using Heron’s formula.

Now using Heron’s formula, you verify this fact by finding the areas of other triangles discussed earlier viz.,

(i) equilateral triangle with side $10\mathrm{cm}$.

(ii) isosceles triangle with unequal side as $8\mathrm{cm}$ and each equal side as $5\mathrm{cm}$.

You will see that

For (i), we have $s=\frac{10+10+10}{2}\mathrm{cm}=15\mathrm{cm}$.

Area of triangle $=\sqrt{15(15-10)(15-10)(15-10)}{\mathrm{cm}}^2$

$$=\sqrt{15\times 5\times 5\times 5}{\mathrm{cm}}^2=25\sqrt{3}{\mathrm{cm}}^2$$

For (ii), we have $s=\frac{8+5+5}{2}\mathrm{cm}=9\mathrm{cm}$

Area of triangle $=\sqrt{9(9-8)(9-5)(9-5)}{\mathrm{cm}}^2=\sqrt{9\times 1\times 4\times 4}{\mathrm{cm}}^2=12{\mathrm{cm}}^2$.

Let us now solve some more examples:

Example 1 : Find the area of a triangle, two sides of which are $8\mathrm{cm}$ and $11\mathrm{cm}$ and the perimeter is $32\mathrm{cm}$ (see Fig. 10.3).

Fig. 10.3

Solution : Here we have perimeter of the triangle $=32\mathrm{cm},a=8\mathrm{cm}$ and $b=11\mathrm{cm}$.

Third side $c=32\mathrm{cm}-(8+11)\mathrm{cm}=13\mathrm{cm}$

So, $2s=32$, i.e., $s=16\mathrm{cm}$, $$\begin{array}{rl}& s-a=(16-8)\mathrm{cm}=8\mathrm{cm},\\ & s-b=(16-11)\mathrm{cm}=5\mathrm{cm},\\ & s-c=(16-13)\mathrm{cm}=3\mathrm{cm}\end{array}$$

Therefore, area of the triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

$$=\sqrt{16\times 8\times 5\times 3}{\mathrm{cm}}^2=8\sqrt{30}{\mathrm{cm}}^2$$

Example 2 : A triangular park $ABC$ has sides $120\mathrm{m},80\mathrm{m}$ and $50\mathrm{m}$ (see Fig. 10.4). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space $3\mathrm{m}$ wide for a gate on one side.

Fig. 10.4

Solution : For finding area of the park, we have

$$\begin{array}{rl}& 2s=50\mathrm{m}+80\mathrm{m}+120\mathrm{m}=250\mathrm{m}.\\ \text{ i.e., }& s=125\mathrm{m}\end{array}$$

Now, $s-a=(125-120)\mathrm{m}=5\mathrm{m}$,

$$\begin{array}{rl}& s-b=(125-80)\mathrm{m}=45\mathrm{m},\\ & s-c=(125-50)\mathrm{m}=75\mathrm{m}.\end{array}$$

Therefore, area of the park $=\sqrt{s(s-a)(s-b)(s-c)}$

$$\begin{array}{rlr}& =\sqrt{125\times 5\times 45\times 75}{\mathrm{m}}^2& =375\sqrt{15}{\mathrm{m}}^2\end{array}$$

Also, perimeter of the park $=\mathrm{AB}+\mathrm{BC}+\mathrm{CA}=250\mathrm{m}$

Therefore, length of the wire needed for fencing $=250\mathrm{m}-3\mathrm{m}$ (to be left for gate)

$$=247\mathrm{m}$$

And so the cost of fencing $=20rupees\times 247=4940$ rupees

Example 3 : The sides of a triangular plot are in the ratio of $3:5:7$ and its perimeter is $300\mathrm{m}$. Find its area.

Solution : Suppose that the sides, in metres, are $3x,5x$ and $7x$ (see Fig. 10.5).

Then, we know that $3x+5x+7x=300$ (perimeter of the triangle)

Therefore, $15x=300$, which gives $x=20$.

So the sides of the triangle are $3\times 20\mathrm{m},5\times 20\mathrm{m}$ and $7\times 20\mathrm{m}$

i.e., $60\mathrm{m},100\mathrm{m}$ and $140\mathrm{m}$.

Can you now find the area [Using Heron’s formula]?

We have $s=\frac{60+100+140}{2}\mathrm{m}=150\mathrm{m}$,

Fig. 10.5

and area will be $$\begin{array}{rl}& \sqrt{150(150-60)(150-100)(150-140)}{\mathrm{m}}^2\\ & =\sqrt{150\times 90\times 50\times 10}{\mathrm{m}}^2\\ & =1500\sqrt{3}{\mathrm{m}}^2\end{array}$$

EXERCISE 10.1

1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ’ $a$ ‘. Find the area of the signal board, using Heron’s formula. If its perimeter is $180\mathrm{cm}$, what will be the area of the signal board?

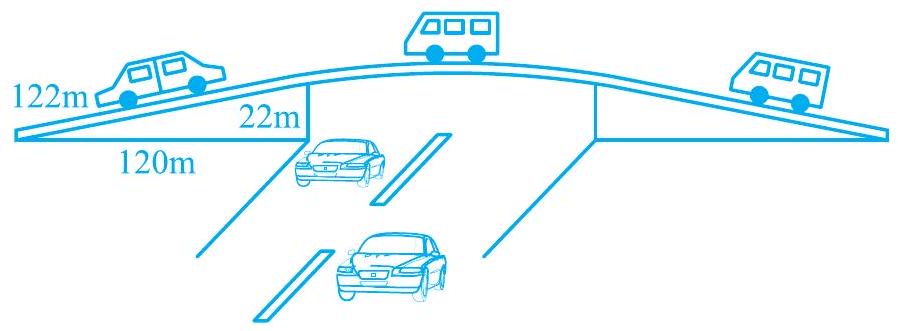
2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are $122\mathrm{m},22\mathrm{m}$ and $120\mathrm{m}$ (see Fig. 10.6). The advertisements yield an earning of ₹ 5000 per ${\mathrm{m}}^2$ per year. A company hired one of its walls for 3 months. How much rent did it pay?

Fig. 10.6

3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREENAND CLEAN” (see Fig. 10.7). If the sides of the wall are $15\mathrm{m},11\mathrm{m}$ and $6\mathrm{m}$, find the area painted in colour.

Fig. 10.7

4. Find the area of a triangle two sides of which are $18\mathrm{cm}$ and $10\mathrm{cm}$ and the perimeter is $42\mathrm{cm}$.

5. Sides of a triangle are in the ratio of $12:17:25$ and its perimeter is $540\mathrm{cm}$. Find its area.

6. An isosceles triangle has perimeter $30\mathrm{cm}$ and each of the equal sides is $12\mathrm{cm}$. Find the area of the triangle.

10.2 Summary

In this chapter, you have studied the following points :

1. Area of a triangle with its sides as $a,b$ and $c$ is calculated by using Heron’s formula, stated as

$$\begin{array}{rl}\text{ Area of triangle }& =\sqrt{s(s-a)(s-b)(s-c)}\\ \text{where}s& =\frac{a+b+c}{2}\end{array}$$