10.1 त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा

हम जानते हैं कि जब त्रिभुज की ऊंचाई दी जाती है तो उसका क्षेत्रफल $\frac{1}{2}\times$ आधार $\times$ ऊंचाई होता है। अब मान लीजिए कि हम एक विषमबाहु त्रिभुज की भुजाओं की लंबाई जानते हैं, ऊँचाई नहीं। क्या आप अब भी इसका क्षेत्रफल ज्ञात कर सकते हैं? उदाहरण के लिए, आपके पास एक त्रिकोणीय पार्क है जिसकी भुजाएँ 40 $\mathrm{m},32\mathrm{m}$, और $24\mathrm{m}$ हैं। आप इसके क्षेत्रफल की गणना कैसे करेंगे? निश्चित रूप से यदि आप सूत्र लागू करना चाहते हैं, तो आपको इसकी ऊंचाई की गणना करनी होगी। लेकिन ऊंचाई की गणना करने के लिए हमारे पास कोई सुराग नहीं है। ऐसा करने का प्रयास करें. यदि आप इसे प्राप्त नहीं कर पा रहे हैं तो अगले भाग पर जाएँ।

हीरोन का जन्म संभवतः मिम्र में अलेक्जेंड्रिया नामक स्थान पर हुआ। उन्होंने अनुप्रायोगिक गणित (applied mathematics) पर कार्य किया। उनका गणितीय और भौतिकीय विषयों पर कार्य इतना अधिक और विभिन्न प्रकार का था कि उन्हें इन क्षेत्रों का एक विश्वकोण संबंधी (encyclopedic) लेखक समझा जाता था। उनका ज्यामितीय कार्य मुख्यतः मेन्सुरेशन ( क्षेत्रमिति) की समस्याओं से संबंधित था। यह कार्य तीन पुस्तकों में लिखा गया है। पुस्तक 1 में, वर्गों, आयतों, त्रिभुजों, समलंबों, अनेक प्रकार के विशिष्ट चतुर्भुजों, सम बहुभुजों, वृत्तों के क्षेत्रफलों, बेलनों, शंकुओं, गोलों, इत्यादि के पृष्ठीय क्षेत्रफलों का वर्णन है।>इसी पुस्तक में, हीरोन ने त्रिभुज की तीनों भुजाओं के पदों में उसके (10 सा०यू०पू०-75 सा०्यू०ू०) क्षेत्रफल का प्रसिद्ध (या सुपरिचित) सूत्र प्रतिपादित किया है।

आकृति 10.1

हीरोन के इस सूत्र को हीरो का सूत्र (Hero’s formula) भी कहा जाता है। इसे नीचे दिया जा रहा है:

$$\text{ त्रिभुज का क्षेत्रफल }=\sqrt{s(s-a)(s-b)(s-c)}$$

जहाँ $a,b$ और $c$ त्रिभुज की भुजाएँ हैं तथा $s=\text{ त्रिभुज का अर्धपरिमाप (semi-perimeter) }=\frac{a+b+c}{2}\text{ है। }$

यह सूत्र उस स्थिति में सहायक होता है, जब त्रिभुज की ऊँचाई सरलता से ज्ञात न हो सकती हो। आइए ऊपर बताए गए त्रिभुजाकार पार्क $\mathrm{ABC}$ का क्षेत्रफल ज्ञात करने के लिए, इस सूत्र का प्रयोग करें (देखिए आकृति 10.2)।

आकृति 10.2

आइए $a=40\mathrm{m},b=24\mathrm{m},c=32\mathrm{m}$ लें

ताकि हमें $$s=\frac{40+24+32}{2}\mathrm{m}=48\mathrm{m}$$ प्राप्त होगा।

अब, $s-a=(48-40)\mathrm{m}=8\mathrm{m}$,

$s-b=(48-24)\mathrm{m}=24\mathrm{m}$,

और $s-c=(48-32)\mathrm{m}=16\mathrm{m}$ हैं।

अतः, पार्क $\mathrm{ABC}$ का क्षेत्रफल

$=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{48\times 8\times 24\times 16}{\mathrm{m}}^2=384{\mathrm{m}}^2$

हम यह भी देखते हैं कि ${32}^2+{24}^2=1024+576=1600={40}^2$ है। अतः, इस पार्क की भुजाएँ एक समकोण त्रिभुज बनाती हैं। सबसे बड़ी, अर्थात् $\mathrm{BC}$, जिसकी लम्बाई $40\mathrm{m}$ है, इस त्रिभुज का कर्ण है तथा $\mathrm{AB}$ और $\mathrm{AC}$ के बीच का कोण ${90}^{\circ }$ होगा।

इसलिए, सूत्र I से हम जाँच कर सकते हैं कि पार्क का क्षेत्रफल $\frac{1}{2}\times 32\times 24{\mathrm{m}}^2=384{\mathrm{m}}^2$.

हम पाते हैं कि यह क्षेत्रफल वही है जो हमें हीरोन के सूत्र से प्राप्त हुआ था।

अब आप पहले चर्चित किए गए अन्य त्रिभुजों के क्षेत्रफलों को हीरोन के सूत्र से ज्ञात करके जाँच कीजिए कि क्षेत्रफल पहले जैसे ही प्राप्त होते हैं। ये त्रिभुज हैं :

(i) $10\mathrm{cm}$ भुजा वाला समबाहु त्रिभुज और

(ii) असमान भुजा $8\mathrm{cm}$ और बराबर भुजाएँ $5\mathrm{cm}$ वाला समद्विबाहु त्रिभुज।

आप देखेंगे कि

(i) के लिए, $s=\frac{10+10+10}{2}\mathrm{cm}=15\mathrm{cm}$

इसलिए, त्रिभुज का क्षेत्रफल $=\sqrt{15(15-10)(15-10)(15-10)}{\mathrm{cm}}^2$

$$=\sqrt{15\times 5\times 5\times 5}{\mathrm{cm}}^2=25\sqrt{3}{\mathrm{cm}}^2$$

(ii) के लिए, $s=\frac{8+5+5}{2}\mathrm{cm}=9\mathrm{cm}$

इसलिए, त्रिभुज का क्षेत्रफल $=\sqrt{9(9-8)(9-5)(9-5)}{\mathrm{cm}}^2=\sqrt{9\times 1\times 4\times 4}{\mathrm{cm}}^2=12{\mathrm{cm}}^2$.

आइए अब कुछ उदाहरण लें।

उदाहरण 1 : एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ $8\mathrm{cm}$ और $11\mathrm{cm}$ हैं और जिसका परिमाप $32\mathrm{cm}$ है (देखिए आकृति 10.3)।

आकृति 10.3

हल : यहाँ, परिमाप $=32\mathrm{cm},a=8\mathrm{cm}$ और $b=11\mathrm{cm}$ है।

इसलिए, तीसरी भुजा $c=32\mathrm{cm}-(8+11)\mathrm{cm}=13\mathrm{cm}$

अब, $2s=32$ है। इसलिए $s=16\mathrm{cm}$, $$\begin{array}{rl}& s-a=(16-8)\mathrm{cm}=8\mathrm{cm},\\ & s-b=(16-11)\mathrm{cm}=5\mathrm{cm},\\ & s-c=(16-13)\mathrm{cm}=3\mathrm{cm}\end{array}$$

इसलिए, त्रिभुज का क्षेत्रफल $=\sqrt{s(s-a)(s-b)(s-c)}$

$$=\sqrt{16\times 8\times 5\times 3}{\mathrm{cm}}^2=8\sqrt{30}{\mathrm{cm}}^2$$

उदाहरण 2: एक त्रिभुजाकार पार्क $\mathrm{ABC}$ की भुजाएँ $120\mathrm{m},80\mathrm{m}$ और $50\mathrm{m}$ हैं (देखिए आकृति 10.4)। एक मालिन धनिया को इसके चारों ओर एक बाड़ लगानी है और इसके अंदर घास उगानी है। उसे कितने क्षेत्रफल में घास उगानी है? एक ओर $3\mathrm{m}$ चौड़े एक फाटक के लिए स्थान छोड़ते हुए इसके चारों ओर ₹ 20 प्रति मीटर की दर से काँटेदार बाड़ लगाने का व्यय भी ज्ञात कीजिए।

आकृति 10.4

हल : पार्क का क्षेत्रफल ज्ञात करने के लिए, हमें प्राप्त है :

$$2s=50\mathrm{m}+80\mathrm{m}+120\mathrm{m}=250\mathrm{m}$$ अर्थात् $s=125\mathrm{m}$

इसलिए, $s-a=(125-120)\mathrm{m}=5\mathrm{m}$,

$$\begin{array}{rl}& s-b=(125-80)\mathrm{m}=45\mathrm{m},\\ & s-c=(125-50)\mathrm{m}=75\mathrm{m}\end{array}$$

अतः, घास उगाने के लिए क्षेत्रफल $=\sqrt{s(s-a)(s-b)(s-c)}$

$$\begin{array}{rlr}& =\sqrt{125\times 5\times 45\times 75}{\mathrm{m}}^2& =375\sqrt{15}{\mathrm{m}}^2\end{array}$$

साथ ही, पार्क का परिमाप $=\mathrm{AB}+\mathrm{BC}+\mathrm{CA}=250\mathrm{m}$

अतः, बाड़ लगाने के लिए आवश्यक तार की लम्बाई $=250\mathrm{m}-3\mathrm{m}$ (फाटक के लिए)

$$=247\mathrm{m}$$

इसलिए, बाड़ लगाने का व्यय $=20रुपये\times 247=4940$ रुपये

उदाहरण 3 : एक त्रिभुजाकार भूखंड (plot) की भुजाओं का अनुपात $3:5:7$ है और उसका परिमाप $300\mathrm{m}$ है। इस भूखंड का क्षेत्रफल ज्ञात कीजिए।

हल : मान लीजिए भुजाएँ (मीटरों में) $3x,5x$ और $7x$ हैं (देखिए आकृति 10.5)।

तब, हम जानते हैं कि $3x+5x+7x=300$ (त्रिभुज का परिमाप)

इसलिए, $15x=300$ है, जिससे $x=20$ प्राप्त होता है।

इसलिए, त्रिभुज की भुजाएँ $3\times 20\mathrm{m},5\times 20\mathrm{m}$ और $7\times 20\mathrm{m}$ हैं।

अर्थात् ये भुजाएँ $60\mathrm{m},100\mathrm{m}$ और $140\mathrm{m}$ हैं।

क्या आप अब (हीरोन का सूत्र प्रयोग करके) क्षेत्रफल ज्ञात कर सकते हैं?

अब, $s=\frac{60+100+140}{2}\mathrm{m}=150\mathrm{m}$

आकृति 10.5

इसलिए, क्षेत्रफल $=\sqrt{150(150-60)(150-100)(150-140)}{\mathrm{m}}^2$ $$\begin{array}{rl}& =\sqrt{150\times 90\times 50\times 10}{\mathrm{m}}^2\\ & =1500\sqrt{3}{\mathrm{cm}}^2\end{array}$$

प्रश्नावली 10.1

1. एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ’ $a$ ’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप $180\mathrm{cm}$ है, तो इसका क्षेत्रफल क्या होगा?

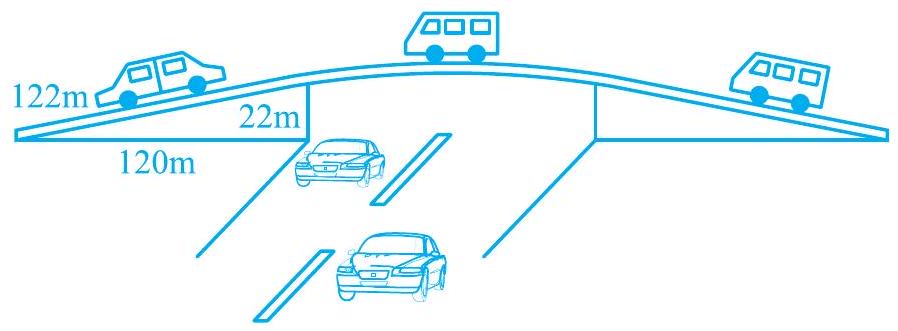
2. किसी फ्लाईओवर (flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ $122\mathrm{m},22\mathrm{m}$ और $120\mathrm{m}$ हैं (देखिए आकृति 10.6)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति ${\mathrm{m}}^2$ की प्राप्ति होती है। एक कम्पनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?

आकृति 10.6

3. किसी पार्क में एक फिसल पट्टी (slide) बनी हुई है। इसकी पार्श्वीय दीवारों (side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर “पार्क को हरा-भरा और साफ रखिए” लिखा हुआ है (देखिए आकृति 10.7)। यदि इस दीवार की विमाएँ $15\mathrm{m}$, $11\mathrm{m}$ और $6\mathrm{m}$ हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।

आकृति 10.7

4. उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ $18\mathrm{cm}$ और $10\mathrm{cm}$ हैं तथा उसका परिमाप $42\mathrm{cm}$ है।

5. एक त्रिभुज की भुजाओं का अनुपात $12:17:25$ है और उसका परिमाप $540\mathrm{cm}$ है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

6. एक समद्विबाहु त्रिभुज का परिमाप $30\mathrm{cm}$ है और उसकी बराबर भुजाएँ $12\mathrm{cm}$ लम्बाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

10.2 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदु का अध्ययन किया है :

1. एक त्रिभुज का क्षेत्रफल जिसकी भुजाएँ इस प्रकार हैं और हेरोन के सूत्र का उपयोग करके गणना की जाती है, जैसा कि कहा गया है

$$\begin{array}{rl}\text{ त्रिभुज का क्षेत्रफल }& =\sqrt{s(s-a)(s-b)(s-c)}\\ \text{होता है जहाँ}s& =\frac{a+b+c}{2}\end{array}$$