Chapter 09 Circles
9.1 Angle Subtended by a Chord at a Point
You have already studied about circles and its parts in Class VI.
Take a line segment

Fig. 9.1

Fig. 9.2
Let us examine the relationship between the size of the chord and the angle subtended by it at the centre. You may see by drawing different chords of a circle and angles subtended by them at the centre that the longer is the chord, the bigger will be the angle subtended by it at the centre. What will happen if you take two equal chords of a circle? Will the angles subtended at the centre be the same or not?
Draw two or more equal chords of a circle and measure the angles subtended by them at the centre (see Fig.9.3). You will find that the angles subtended by them at the centre are equal. Let us give a proof of this fact.

Fig. 9.3
Theorem 9.1 : Equal chords of a circle subtend equal angles at the centre.
Proof : You are given two equal chords AB and CD of a circle with centre O (see Fig.9.4). You want to prove that

Fig. 9.4
In triangles
Therefore
This gives
(Corresponding parts of congruent triangles)
Remark : For convenience, the abbreviation CPCT will be used in place of ‘Corresponding parts of congruent triangles’, because we use this very frequently as you will see.
Now if two chords of a circle subtend equal angles at the centre, what can you say about the chords? Are they equal or not? Let us examine this by the following activity:
Take a tracing paper and trace a circle on it. Cut it along the circle to get a disc. At its centre

Fig. 9.5
Though you have seen it for this particular case, try it out for other equal angles too. The chords will all turn out to be equal because of the following theorem:
Theorem 9.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
The above theorem is the converse of the Theorem 9.1. Note that in Fig. 9.4, if you take
Can you now see that
EXERCISE 9.1
1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Show Answer
Solution
A circle is a collection of points which are equidistant from a fixed point. This fixed point is called as the centre of the circle and this equal distance is called as radius of the
circle. And thus, the shape of a circle depends on its radius. Therefore, it can be observed that if we try to superimpose two circles of equal radius, then both circles will cover each other. Therefore, two circles are congruent if they have equal radius. Consider two congruent circles having centre

In
Hence, equal chords of congruent circles subtend equal angles at their centres.
2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Show Answer
Solution
Let us consider two congruent circles (circles of same radius) with centres as 
In
Hence, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
9.2 Perpendicular from the Centre to a Chord
Activity : Draw a circle on a tracing paper. Let
Yes it will. So MA=MB.

Fig. 9.6
Give a proof yourself by joining
Theorem 9.3 : The perpendicular from the centre of a circle to a chord bisects the chord.
What is the converse of this theorem? To write this, first let us be clear what is assumed in Theorem 9.3 and what is proved. Given that the perpendicular from the centre of a circle to a chord is drawn and to prove that it bisects the chord. Thus in the converse, what the hypothesis is ‘if a line from the centre bisects a chord of a circle’ and what is to be proved is ’the line is perpendicular to the chord’. So the converse is:
Theorem 9.4 : The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Is this true? Try it for few cases and see. You will see that it is true for these cases. See if it is true, in general, by doing the following exercise. We will write the stages and you give the reasons.
Let

Fig. 9.7
Therefore,
This gives
9.3 Equal Chords and their Distances from the Centre
Let

Fig. 9.8
The length of the perpendicular from a point to a line is the distance of the line from the point.
Note that if the point lies on the line, the distance of the line from the point is zero.
A circle can have infinitely many chords. You may observe by drawing chords of a circle that longer chord is nearer to the centre than the smaller chord. You may observe it by drawing several chords of a circle of different lengths and measuring their distances from the centre. What is the distance of the diameter, which is the longest chord from the centre? Since the centre lies on it, the distance is zero. Do you think that there is some relationship between the length of chords and their distances from the centre? Let us see if this is so.

Fig. 9.9
Activity : Draw a circle of any radius on a tracing paper. Draw two equal chords
Theorem 9.5 : Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Next, it will be seen whether the converse of this theorem is true or not. For this, draw a circle with centre O. From the centre O, draw two line segments OL and OM of equal length and lying inside the circle [see Fig. 9.10(i)]. Then draw chords PQ and RS of the circle perpendicular to OL and OM respectively [see Fig 9.10(ii)]. Measure the lengths of PQ and RS. Are these different? No, both are equal. Repeat the activity for more equal line segments and drawing the chords perpendicular to them. This verifies the converse of the Theorem 9.5 which is stated as follows:

Fig. 9.10
Theorem 9.6 : Chords equidistant from the centre of a circle are equal in length. We now take an example to illustrate the use of the above results:
Example 1 : If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
Solution : Given that

Fig. 9.11
In triangles OLE and OME,
EXERCISE 9.2
1. Two circles of radii
Show Answer
Solution
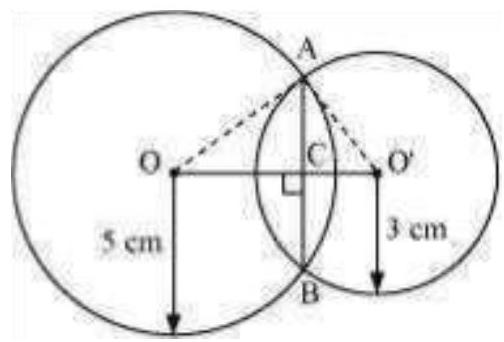
Let the radius of the circle centered at
It is given that,
Let
In
From equations (1) and (2), we obtain
Therefore, the common chord will pass through the centre of the smaller circle i.e., O’ and hence, it will be the diameter of the smaller circle.
Length of the common chord
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Show Answer
Solution
Let
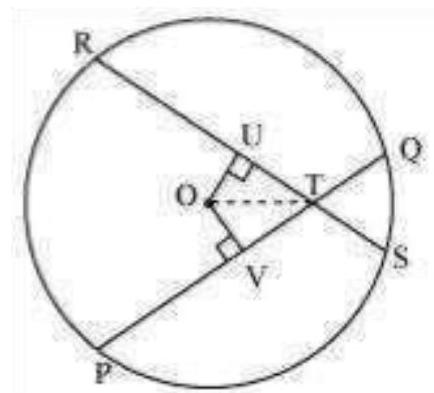
Draw perpendiculars OV and OU on these chords.
In
OT
It is given that,
On adding equations (1) and (3), we obtain
On subtracting equation (4) from equation (2), we obtain
Equations (4) and (5) indicate that the corresponding segments of chords PQ and RS are congruent to each other.
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Show Answer
Solution
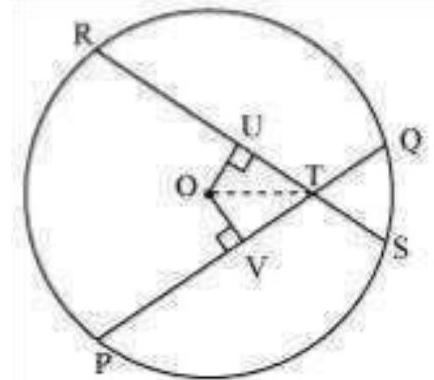
Let
Draw perpendiculars OV and OU on these chords.
In
OT
Therefore, it is proved that the line joining the point of intersection to the centre makes equal angles with the chords.
4. If a line intersects two concentric circles (circles with the same centre) with centre
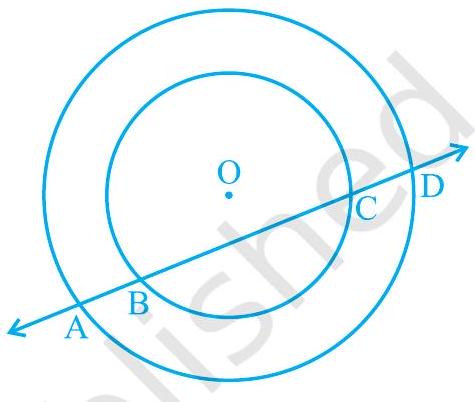
Fig. 9.12
Show Answer
Solution
Let us draw a perpendicular OM on line AD.
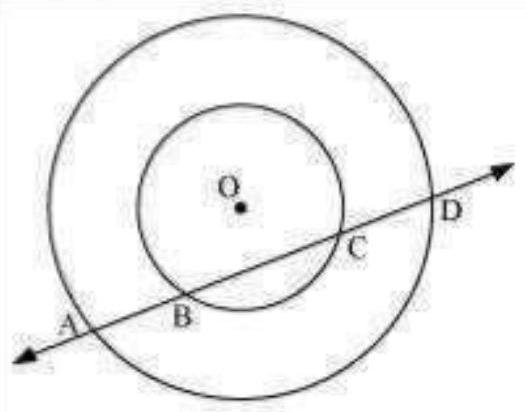
It can be observed that
We know that perpendicular drawn from the centre of the circle bisects the chord.
On subtracting equation (2) from (1), we obtain
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius
Show Answer
Solution
Draw perpendiculars
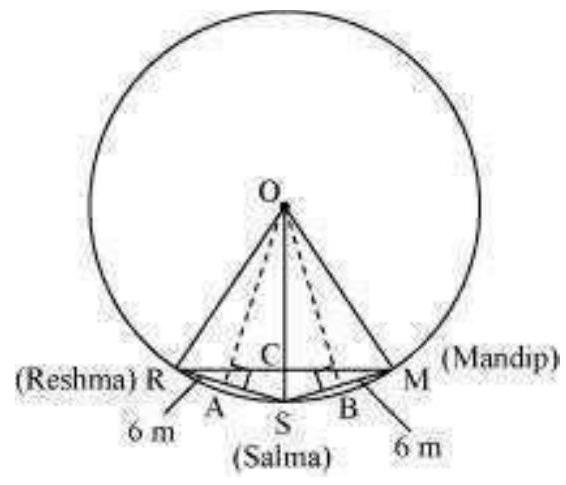
In
ORSM will be a kite (
RCS will be of
Area of
Therefore, the distance between Reshma and Mandip is
6. A circular park of radius
Show Answer
Solution
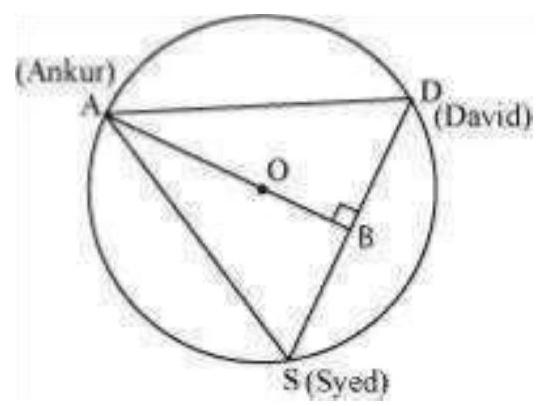
It is given that
Therefore,
Medians of equilateral triangle pass through the circum centre
In
Therefore, the length of the string of each phone will be
9.4 Angle Subtended by an Arc of a Circle
You have seen that the end points of a chord other than diameter of a circle cuts it into two arcs - one major and other minor. If you take two equal chords, what can you say about the size of arcs? Is one arc made by first chord equal to the corresponding arc made by another chord? In fact, they are more than just equal in length. They are congruent in the sense that if one arc is put on the other, without bending or twisting, one superimposes the other completely.
You can verify this fact by cutting the arc, corresponding to the chord

Fig. 9.13
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Also the angle subtended by an arc at the centre is defined to be angle subtended by the corresponding chord at the centre in the sense that the minor arc subtends the angle and the major arc subtends the reflex angle. Therefore, in Fig 9.14, the angle subtended by the minor arc
In view of the property above and Theorem 9.1, the following result is true:

Fig. 9.14
Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre.
Therefore, the angle subtended by a chord of a circle at its centre is equal to the angle subtended by the corresponding (minor) arc at the centre. The following theorem gives the relationship between the angles subtended by an arc at the centre and at a point on the circle.
Theorem 9.7 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof : Given an arc PQ of a circle subtending angles POQ at the centre

(i)

(ii)

(iii)
Fig. 9.15
Consider the three different cases as given in Fig. 9.15. In (i), arc PQ is minor; in (ii), arc PQ is a semicircle and in (iii), arc PQ is major.
Let us begin by joining
In all the cases,
because an exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Also in
Therefore,
This gives
Similarly,
From (1) and (2),
This is the same as
For the case (iii), where
Remark : Suppose we join points
In Theorem 9.7, A can be any point on the remaining part of the circle. So if you take any other point
Therefore,

Fig. 9.16
This proves the following:
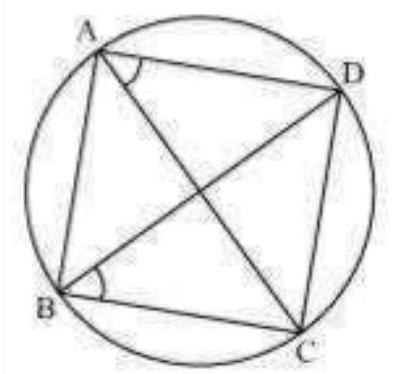
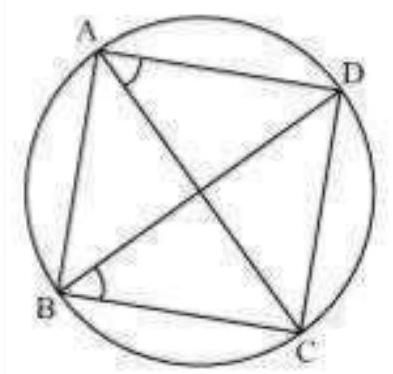
Theorem 9.8 : Angles in the same segment of a circle are equal.
Again let us discuss the case (ii) of Theorem 10.8 separately. Here
Therefore, you find another property of the circle as:
Angle in a semicircle is a right angle.
The converse of Theorem 9.8 is also true. It can be stated as:
Theorem 9.9 : If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
You can see the truth of this result as follows:
In Fig. 9.17,

Fig. 9.17
To show that the points
If points
But it is given that
Therefore,
This is not possible unless
Similarly, E’ should also coincide with D.
9.5 Cyclic Quadrilaterals
A quadrilateral

Fig. 9.18
| S.No. of Quadrilateral | ||||||
|---|---|---|---|---|---|---|
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. | ||||||
| 5. | ||||||
| 6. |
What do you infer from the table?
You find that
Theorem 9.10 : The sum of either pair of opposite angles of a cyclic quadrilateral is
In fact, the converse of this theorem, which is stated below is also true.
Theorem 9.11 : If the sum of a pair of opposite angles of a quadrilateral is
You can see the truth of this theorem by following a method similar to the method adopted for Theorem 9.9.
Example 2 : In Fig. 9.19,

Fig. 9.19
Solution : Join OC, OD and BC.
Triangle ODC is equilateral
Therefore,
Now,
This gives
Again,
So,
Which gives
Example 3 : In Fig 9.20, ABCD is a cyclic quadrilateral in which

Fig. 9.20
Solution :
But
(Opposite angles of a cyclic quadrilateral)
So,
Example 4 : Two circles intersect at two points A and

Fig. 9.21
Solution : Join AB.
So,
Therefore,
Example 5 : Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.
Solution : In Fig. 9.22, ABCD is a quadrilateral in which the angle bisectors

Fig. 9.22
and
Therefore,
Therefore, by Theorem 9.11, the quadrilateral EFGH is cyclic.
EXERCISE 9.3
1. In Fig. 9.23,
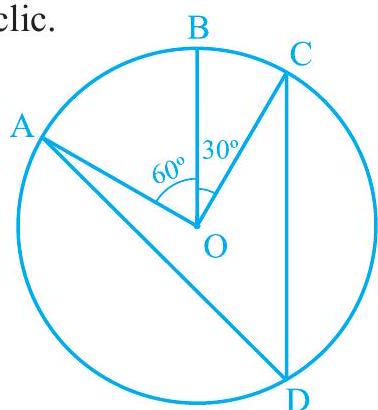
Fig. 9.23
Show Answer
Solution
It can be observed that
We know that angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Show Answer
Solution
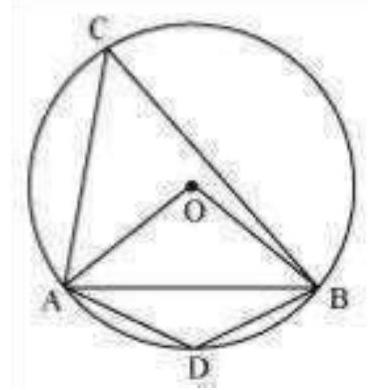
In
Therefore, each interior angle of this triangle will be of
In cyclic quadrilateral
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are
3. In Fig. 9.24,
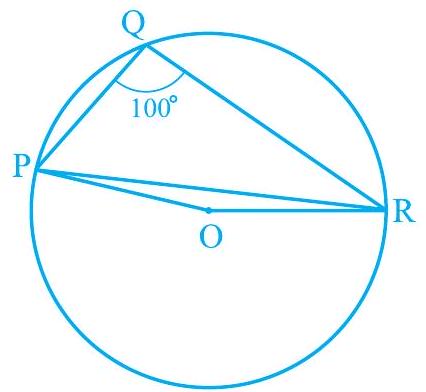
Fig. 9.24
Show Answer
Solution
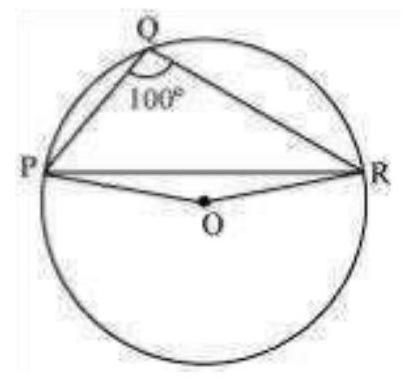
Consider PR as a chord of the circle.
Take any point
PQRS is a cyclic quadrilateral.
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
In
4. In Fig. 9.25,
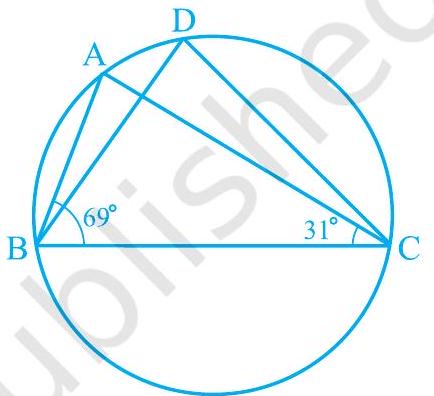
Fig. 9.25
Show Answer
Solution5. In Fig. 9.26, A, B, C and D are four points on a circle.
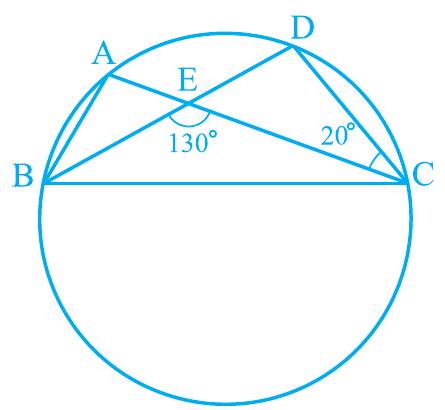
Fig. 9.26
Show Answer
Solution
For chord CD,
However,
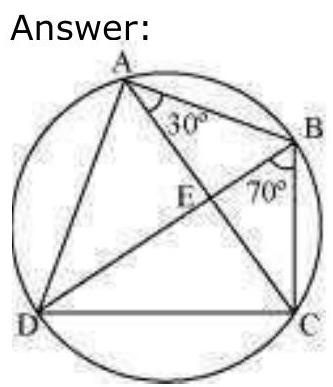
6.
Show Answer
Solution
CD + BAD
We have,
7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Show Answer
Solution
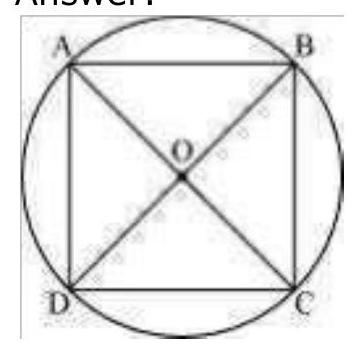
Let
(Considering
Each interior angle of a cyclic quadrilateral is of
8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Show Answer
Solution
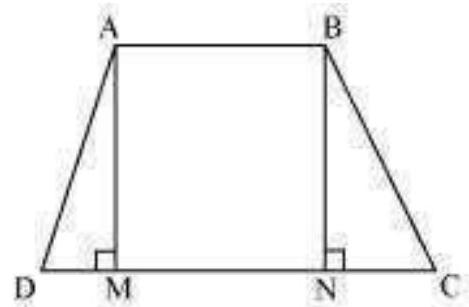
Consider a trapezium
Draw
In
This equation shows that the opposite angles are supplementary.
Therefore,
9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at
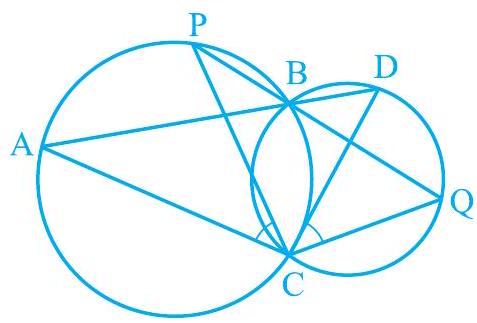
Fig. 9.27
Show Answer
Solution
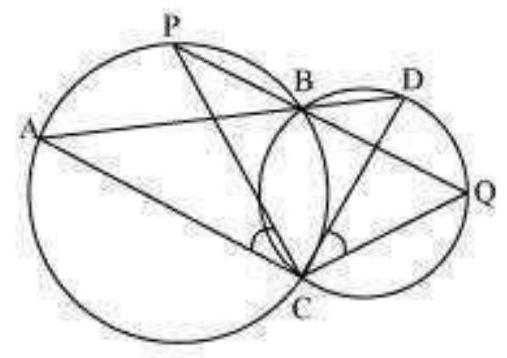
Join chords AP and DQ.
For chord AP,
For chord DQ,
PBQ are line segments intersecting at
From equations ( 1 ), ( 2 ), and ( 3 ), we obtain
10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Show Answer
Solution
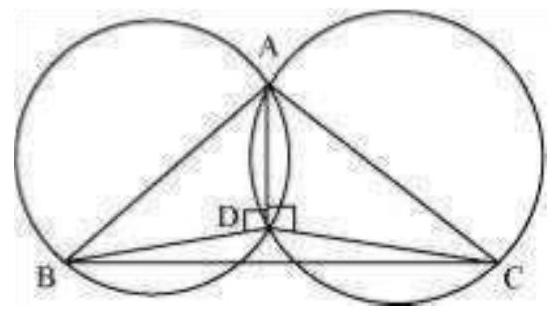
Consider a
Two circles are drawn while taking
Let they intersect each other at
Join AD.
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point
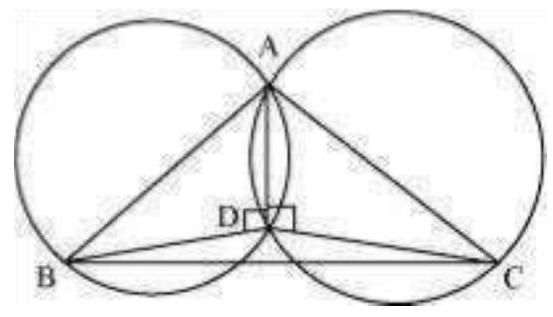
11.
Show Answer
Solution
In
In
Adding equations (1) and (2), we obtain
However, it is given that
From equations (3) and (4), it can be observed that the sum of the measures of opposite angles of quadrilateral
Consider chord CD.
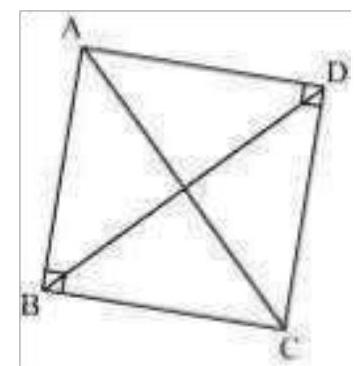
12. Prove that a cyclic parallelogram is a rectangle.
Show Answer
Solution
Let
From equation (1),
Parallelogram
9.6 Summary
In this chapter, you have studied the following points:
1. A circle is the collection of all points in a plane, which are equidistant from a fixed point in the plane.
2. Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.
3. If the angles subtended by two chords of a circle (or of congruent circles) at the centre (corresponding centres) are equal, the chords are equal.
4. The perpendicular from the centre of a circle to a chord bisects the chord.
5. The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
6. Equal chords of a circle (or of congruent circles) are equidistant from the centre (or corresponding centres).
7. Chords equidistant from the centre (or corresponding centres) of a circle (or of congruent circles) are equal.
8. If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major) are congruent.
9. Congruent arcs of a circle subtend equal angles at the centre.
10. The angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.
11. Angles in the same segment of a circle are equal.
12. Angle in a semicircle is a right angle.
13. If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.
14. The sum of either pair of opposite angles of a cyclic quadrilateral is
15. If sum of a pair of opposite angles of a quadrilateral is










