अध्याय 09 वृत्त
9.1 जीवा द्वारा एक बिन्दु पर अंतरित कोण
एक रेखाखंड

आकृति 9.1

आकृति 9.2
आइए हम जीवा की माप तथा उसके द्वारा केन्द्र पर अंतरित कोण में संबंध की जाँच करें। आप एक वृत्त में विभिन्न जीवाएँ खींचकर तथा उनके द्वारा केन्द्र पर अंतरित कोणों को बनाकर देख सकते हैं कि जीवा यदि बड़ी होगी, तो उसके द्वारा केन्द्र पर अंतरित कोण भी बड़ा होगा। क्या होगा यदि आप दो बराबर जीवाएँ लेंगे? क्या केन्द्र पर अंतरित कोण समान होंगे या नहीं?
एक वृत्त की दो या अधिक बराबर जीवाएँ खींचिए तथा केन्द्र पर उनके द्वारा अंतरित कोणों को मापिए (देखिए आकृति 9.3)। आप पाएँगे कि उनके द्वारा केन्द्र पर अंतरित कोण बराबर हैं। आइए इस तथ्य की हम उपपत्ति दें।

आकृति 9.3
प्रमेय 9.1 : वृत्त की बराबर जीवाएँ केन्द्र पर बराबर कोण अंतरित करती हैं।
उपपत्ति : आपको एक वृत्त, जिसका केन्द्र

आकृति 9.4
त्रिभुजों
अतः,
इस प्रकार, हम पाते हैं कि
(सर्वांगसम त्रिभुजों के संगत भाग)
टिप्पणी : सुविधा के लिए ‘सर्वांगसम त्रिभुजों के संगत भाग’ के स्थान पर संक्षेप में CPCT का प्रयोग किया जाएगा, क्योंकि जैसा कि आप देखेंगे कि इसका हम बहुधा प्रयोग करते हैं।
अब यदि एक वृत्त की दो जीवाएँ केन्द्र पर बराबर कोण अंतरित करें, तो उन जीवाओं के बारे में आप क्या कह सकते हैं? क्या वे बराबर हैं अथवा नहीं? आइए हम इसकी निम्न क्रियाकलाप द्वारा जाँच करें।
एक अक्स कागज़ (tracing paper) लीजिए और इस पर एक वृत्त खींचिए। इसे वृत्त के अनुदिश काटकर एक चकती (disc) प्राप्त कीजिए। इसके केन्द्र

आकृति 9.5
यद्यपि आपने इसे एक विशेष दशा में ही देखा है, इसे आप अन्य समान कोणों के लिए दोहराइए। निम्न प्रमेय के कारण सभी जीवाएँ बराबर होंगी:
प्रमेय 9.2 : यदि एक वृत्त की जीवाओं द्वारा केन्द्र पर अंतरित कोण बराबर हों, तो वे जीवाएँ बराबर होती हैं।
उपर्युक्त प्रमेय, प्रमेय 9.1 का विलोम है। ध्यान दीजिए कि आकृति 9.4 में यदि आप
क्या अब आप देख सकते हैं कि
प्रश्नावली 9.1
1. याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
Show Answer
Missing2. सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
Show Answer
Missing9.2 केन्द्र से जीवा पर लम्ब
क्रियाकलाप : एक अक्स कागज पर एक वृत्त खींचिए। माना इसका केन्द्र
हाँ, यह होगा। इसलिए

आकृति 9.6
प्रमेय 9.3 : एक वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
इस प्रमेय का विलोम क्या है? इसको लिखने के लिए, सर्वप्रथम हमें स्पष्ट होना है कि प्रमेय 9.3 में क्या दिया गया है और क्या सिद्ध करना है। दिया है कि केन्द्र से जीवा पर लंब खींचा गया है और सिद्ध करना है कि वह जीवा को समद्विभाजित करता है। अतः विलोम में परिकल्पना है ‘यदि एक केन्द्र से जाने वाली रेखा वृत्त की एक जीवा को समद्विभाजित करे’ और सिद्ध करना है ‘रेखा जीवा पर लम्ब है’। इस प्रकार, विलोम है :
प्रमेय 9.4: एक वृत्त के केन्द्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर लंब होती है।
क्या यह सत्य है? इसको कुछ स्थितियों में प्रयत्न करके देखिए। आप देखेंगे कि यह इन सभी स्थितियों में सत्य है। निम्न अभ्यास करके देखिए कि क्या यह कथन व्यापक रूप में सत्य है। हम इसके कुछ कथन देंगे और आप इनके कारण दीजिए।
मान लीजिए कि एक वृत्त, जिसका केन्द्र

आकृति 9.7
अत:,
इससे प्राप्त होता है:
9.3 समान जीवाएँ और उनकी केन्द्र से दूरियाँ
मान लीजिए

आकृति 9.8
एक बिन्दु से एक रेखा पर लम्ब की लम्बाई रेखा की बिन्दु से दूरी होती है।
ध्यान दीजिए कि यदि बिन्दु रेखा पर स्थित है, तो रेखा की इससे दूरी शून्य है।
एक वृत्त में असंख्य जीवाएँ हो सकती हैं। आप एक वृत्त में जीवाएँ खींचकर जाँच कर सकते हैं कि लंबी जीवा, छोटी जीवा की तुलना में केन्द्र के निकट होती है। इसकी आप विभिन्न लम्बाई की कई जीवाएँ की खींचकर तथा उनकी केन्द्र से दूरियाँ मापकर जाँच कर सकते हैं। व्यास, जो वृत्त की सबसे बड़ी जीवा है, की केन्द्र से क्या दूरी है? क्योंकि केन्द्र इस पर स्थित है, अतः इसकी दूरी शून्य है। क्या आप सोचते हैं कि जीवा की लम्बाई और उसकी केन्द्र से दूरी में कोई संबंध है? आइए देखें कि क्या ऐसा है।

आकृति 9.9
क्रियाकलाप : किसी त्रिज्या का अक्स कागज पर एक वृत्त खींचिए। इसकी दो बराबर जीवाएँ
प्रमेय 9.5 : एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या केन्द्रों से) समान दूरी पर होती है।
अब यह देखा जाए कि क्या इसका विलोम सत्य है अथवा नहीं। इसके लिए केन्द्र

आकृति 9.10
प्रमेय 9.6 : एक वृत्त के केन्द्र से समदूरस्थ जीवाएँ लम्बाई में समान होती हैं। अब हम उपर्युक्त परिणामों पर आधारित एक उदाहरण लेते हैं।
उदाहरण 1 : यदि एक वृत्त की दो प्रतिच्छेदी जीवाएँ प्रतिच्छेद बिन्दु से जाने वाले व्यास से समान कोण बनाएँ, तो सिद्ध कीजिए कि वे जीवाएँ बराबर हैं।
हल : दिया है कि एक वृत्त, जिसका केन्द्र

आकृति 9.11
त्रिभुजों OLE तथा OME में,
प्रश्नावली 9.2
1.
Show Answer
Missing2. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
Show Answer
Missing3. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
Show Answer
Missing4. यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र
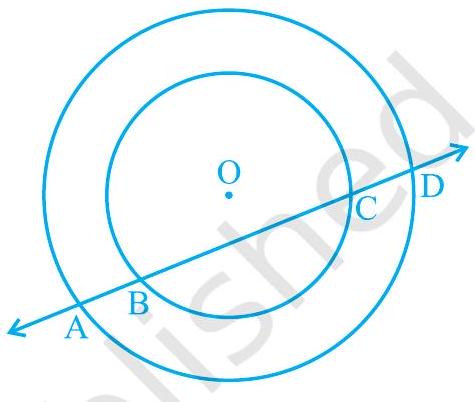
आकृति 9.12
Show Answer
Missing5. एक पार्क में बने
Show Answer
Missing6.
Show Answer
Missing9.4 एक वृत्त के चाप द्वारा अंतरित कोण
आपने देखा है कि एक जीवा के अंत बिन्दु (व्यास के अतिरिक्त) वृत्त को दो चापों में एक (दीर्घ तथा दूसरा लघु) विभाजित करते हैं। यदि आप बराबर जीवाएँ लें, तो आप उन चापों की मापों के बारे में क्या कह सकते हैं? क्या एक जीवा द्वारा बना चाप दूसरी जीवा के द्वारा बने चाप के बराबर है? वास्तव में, ये बराबर लम्बाई से भी कुछ अधिक है। यह इस अर्थ में, कि यदि एक चाप को दूसरे चाप के ऊपर रखा जाए, तो बिना ऐंठे या मोड़े वे एक दूसरे को पूर्णतया ढक लेंगे।
इस तथ्य को आप जीवा

आकृति 9.13
यदि किसी वृत्त की दो जीवाएँ बराबर हों, तो उनके संगत चाप सवरंगसम होते हैं तथा विलोमतः यदि दो चाप सर्वांगसम हों, तो उनके संगत जीवाएँ बराबर होती हैं।
चाप द्वारा केन्द्र पर अंतरित कोण भी संगत जीवा द्वारा केन्द्र पर अंतरित कोण से इस अर्थ में परिभाषित किया जाता है कि लघु चाप कोण को अंतरित करता है और दीर्घ चाप संगत प्रतिवर्ती कोण अंतरित करता है। अतः आकृति 9.14 में, लघु चाप
उपरोक्त गुण एवं प्रमेय 9.1 के संदर्भ में निम्न परिणाम सत्य है :

आकृति 9.14
किसी वृत्त के सर्वांगसम चाप (या बराबर चाप) केन्द्र पर बराबर कोण अंतरित करते हैं।
अतः, किसी वृत्त की जीवा द्वारा केन्द्र पर अंतरित कोण संगत (लघु) चाप द्वारा केन्द्र पर अंतरित कोण के बराबर होता है। निम्न प्रमेय एक चाप द्वारा केन्द्र पर अंतरित कोण तथा वृत्त के किसी बिन्दु पर अंतरित कोण में संबंध देती है।
प्रमेय 9.7 : एक चाप द्वारा केन्द्र पर अंतरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अंतरित कोण का दुगुना होता है।
उपपत्ति : एक वृत्त का चाप

(i)

(ii)

(iii)
आकृति 9.15
आकृति 9.15 में दी गई तीन विभिन्न स्थितियों पर विचार कीजिए।
(i) में चाप
आइए हम
सभी स्थितियों में,
( क्योंकि त्रिभुज का बहिष्कोण उसके दो अभिमुख अंतः कोणों के योग के बराबर होता है।)
साथ ही
अतः,
इससे प्राप्त होता है:
इसी प्रकार,
(1) और (2) से,
अर्थात्,
स्थिति (iii) के लिए, जहाँ PQ दीर्घ चाप है, (3) के स्थान पर
प्रतिवर्ती कोण
टिप्पणी : मान लीजिए कि उपर्युक्त आकृतियों में हम
प्रमेय 9.7 में वृत्त के शेष भाग पर कोई भी बिन्दु
अतः,

आकृति 9.16
यह निम्न को सिद्ध करता है :
प्रमेय 9.8 : एक ही वृत्तखंड के कोण बराबर होते हैं।
आइए अब प्रमेय 9.8 की स्थिति (ii) की अलग से विवेचना करें। यहाँ
इस प्रकार, आप वृत्त का एक और गुण पाते हैं जो निम्न है:
अर्धवृत्त का कोण समकोण होता है।
प्रमेय 9.8 का विलोम भी सत्य है, जिसका इस प्रकार कथन दिया जा सकता है:
प्रमेय 9.9: यदि दो बिन्दुओं को मिलाने वाला रेखाखंड, उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिन्दुओं पर समान कोण अंतरित करे, तो चारों बिन्दु एक वृत्त पर स्थित होते हैं (अर्थात् वे चक्रीय होते हैं)।
आप इस कथन की सत्यता निम्न प्रकार से देख सकते हैं :
आकृति 9.17 में

आकृति 9.17
यह दर्शाने के लिए कि बिन्दु
यदि बिन्दु
परन्तु दिया है कि
अत:,
यह तब तक संभव नहीं है जब तक
इसी प्रकार,
9.5 चक्रीय चतुर्भुज
एक चतुर्भुज

आकृति 9.18
| चतुर्भुज की क्रम संख्या | ||||||
|---|---|---|---|---|---|---|
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. | ||||||
| 5. | ||||||
| 6. |
इस सारणी से आप क्या निष्कर्ष निकालते हैं?
यदि मापने में कोई त्रुटि न हुई हो, तो यह निम्न को सत्यापित करता है:
प्रमेय 9.10 : चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग
वास्तव में इस प्रमेय का विलोम, जिसका कथन निम्न प्रकार से है, भी सत्य है:
प्रमेय 9.11: यदि किसी चतुर्भुज के सम्मुख कोणों के एक युग्म का योग
इस प्रमेय की सत्यता आप प्रमेय 9.9 में दी गई विधि की तरह से जाँच सकते हैं।
उदाहरण 2 : आकृति 9.19 में,

आकृति 9.19
हल :
त्रिभुज
इससे प्राप्त होता है:
पुन:
इसलिए,
जिससे
उदाहरण 3 : आकृति 9.20 में,

आकृति 9.20
हल :
अत:,
परन्तु,
(चक्रीय चतुर्भुज के सम्मुख कोण)
इसलिए,
उदाहरण 4 : दो वृत्त दो बिन्दुओं

आकृति 9.21
हल :
इसलिए,
अतः,
उदाहरण 5 : सिद्ध कीजिए कि किसी चतुर्भुज के अंतः कोणों के समद्विभाजकों से बना चतुर्भुज (यदि संभव हो) चक्रीय होता है।
हल : आकृति 9.22 में,

आकृति 9.22
तथा
इसलिए, प्रमेय 9.11 से चतुर्भुज
प्रश्नावली 9.3
1. आकृति 9.23 में, केन्द्र
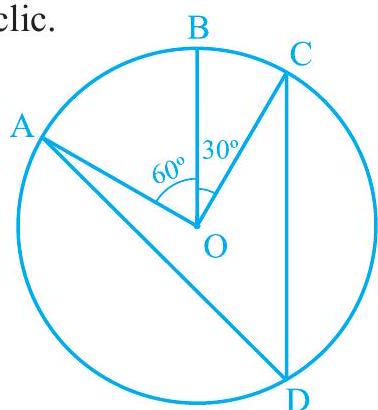
आकृति 9.23
Show Answer
Missing2. किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अंतरित कोण ज्ञात कीजिए।
Show Answer
Missing3. आकृति 9.24 में,
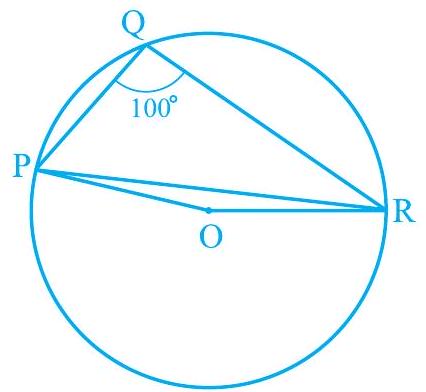
आकृति 9.24
Show Answer
Missing4. आकृति 9.25 में,
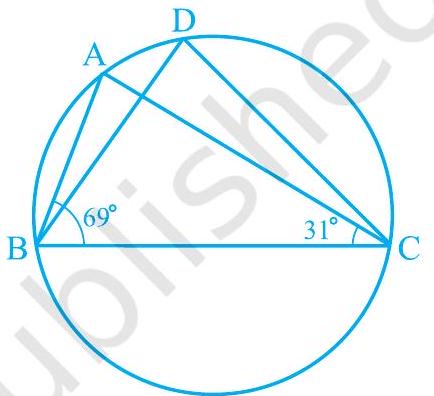
आकृति 9.25
Show Answer
Missing- आकृति 9.26 में, एक वृत्त पर
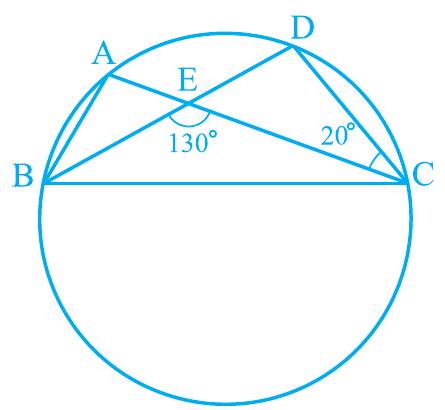
आकृति 9.26
Show Answer
Missing6.
Show Answer
Missing7. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
Show Answer
Missing8. यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
Show Answer
Missing9. दो वृत्त दो बिन्दुओं
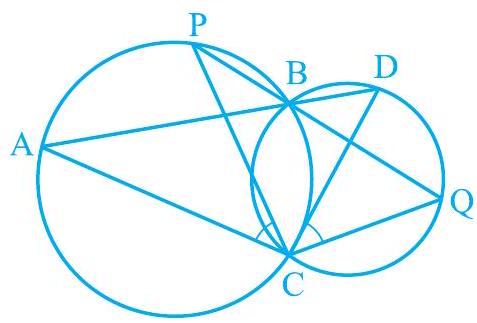
आकृति 9.27
Show Answer
Missing10. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
Show Answer
Missing11. उभयनिष्ठ कर्ण
Show Answer
Missing12. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।
Show Answer
Missing9.6 सारांश
इस अध्याय में, आपने निम्न बिन्दुओं का अध्ययन किया है :
1. एक वृत्त किसी तल के उन सभी बिन्दुओं का समूह होता है, जो तल के एक स्थिर बिन्दु से समान दूरी पर हों।
2. एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र (या संगत केन्द्रों) पर बराबर कोण अंतरित करती हैं।
3. यदि किसी वृत्त की (या सर्वांगसम वृत्तों की) दो जीवाएँ केन्द्र पर (या संगत केन्द्रों पर) बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
4. किसी वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है।
5. केन्द्र से होकर जाने वाली और किसी जीवा को समद्विभाजित करने वाली रेखा जीवा पर लम्ब होती है।
6. एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या संगत केन्द्रों से) समान दूरी पर होती हैं।
7. एक वृत्त के केन्द्र (या सर्वांगसम वृत्तों के केन्द्रों) से समान दूरी पर स्थित जीवाएं बराबर होती हैं।
8. यदि किसी वृत्त के दो चाप सर्वांगसम हों, तो उनकी संगत जीवाएँ बराबर होती हैं और विलोमतः यदि किसी वृत्त की दो जीवाएँ बराबर हों, तो उनके संगत चाप (लघु, दीर्घ) सर्वांगसम होते हैं।
9. किसी वृत्त की सर्वांगसम चाप केन्द्र पर बराबर कोण अंतरित करते हैं।
10. किसी चाप द्वारा केन्द्र पर अंतरित कोण उसके द्वारा वृत्त के शेष भाग के किसी बिन्दु पर अंतरित कोण का दुगुना होता है।
11. एक वृत्तखंड में बने कोण बराबर होते हैं।
12. अर्धवृत्त का कोण समकोण होता है।
13. यदि दो बिन्दुओं को मिलाने वाला रेखाखंड उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिन्दुओं पर समान कोण अंतरित करे, तो चारों बिन्दु एक वृत्त पर स्थित होते हैं।
14. चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग
15. यदि किसी चतुर्भुज के सम्मुख कोणों के किसी एक युग्म का योग










