Chapter 08 Quadrilaterals
8.1 Properties of a Parallelogram
You have already studied quadrilaterals and their types in Class VIII. A quadrilateral has four sides, four angles and four vertices. A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel. Let us perform an activity.
Cut out a parallelogram from a sheet of paper and cut it along a diagonal (see Fig. 8.1). You obtain two triangles. What can you say about these triangles?
Place one triangle over the other. Turn one around, if necessary. What do you observe?
Observe that the two triangles are congruent to each other.

Fig. 8.1
Repeat this activity with some more parallelograms. Each time you will observe that each diagonal divides the parallelogram into two congruent triangles. Let us now prove this result.
Theorem 8.1 : A diagonal of a parallelogram divides it into two congruent triangles.
Proof : Let

Fig. 8.2
In
So,
Also,
So,
and
So,
or, diagonal
Now, measure the opposite sides of parallelogram
You will find that
This is another property of a parallelogram stated below:
Theorem 8.2 : In a parallelogram, opposite sides are equal.
You have already proved that a diagonal divides the parallelogram into two congruent triangles; so what can you say about the corresponding parts say, the corresponding sides? They are equal.
So,
Now what is the converse of this result? You already know that whatever is given in a theorem, the same is to be proved in the converse and whatever is proved in the theorem it is given in the converse. Thus, Theorem 8.2 can be stated as given below :
If a quadrilateral is a parallelogram, then each pair of its opposite sides is equal. So its converse is :
Theorem 8.3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Can you reason out why?
Let sides

Fig. 8.3
Clearly,
So,
and
Can you now say that ABCD is a parallelogram? Why?
You have just seen that in a parallelogram each pair of opposite sides is equal and conversely if each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram. Can we conclude the same result for the pairs of opposite angles?
Draw a parallelogram and measure its angles. What do you observe?
Each pair of opposite angles is equal.
Repeat this with some more parallelograms. We arrive at yet another result as given below.
Theorem 8.4 : In a parallelogram, opposite angles are equal.
Now, is the converse of this result also true? Yes. Using the angle sum property of a quadrilateral and the results of parallel lines intersected by a transversal, we can see that the converse is also true. So, we have the following theorem :
Theorem 8.5 : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
There is yet another property of a parallelogram. Let us study the same. Draw a parallelogram

Fig. 8.4
Measure the lengths of
What do you observe? You will observe that
or,
Repeat this activity with some more parallelograms.
Each time you will find that
So, we have the following theorem :
Theorem 8.6 : The diagonals of a parallelogram bisect each other.
Now, what would happen, if in a quadrilateral the diagonals bisect each other? Will it be aparallelogram? Indeed this is true.
This result is the converse of the result of Theorem 8.6. It is given below:
Theorem 8.7 : If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
You can reason out this result as follows:
Note that in Fig. 8.5, it is given that

Fig. 8.5
So,
Therefore,
From this, we get
Similarly,
Therefore
Let us now take some examples.
Example 1 : Show that each angle of a rectangle is a right angle.
Solution : Let us recall what a rectangle is.
A rectangle is a parallelogram in which one angle is a right angle.
Let
We have to show that
We have,

Fig. 8.6
So,
But,
So,
Now,
(Opposite angles of the parallellogram)
So,
Therefore, each of the angles of a rectangle is a right angle.
Example 2 : Show that the diagonals of a rhombus are perpendicular to each other.
Solution : Consider the rhombus ABCD (see Fig. 8.7).
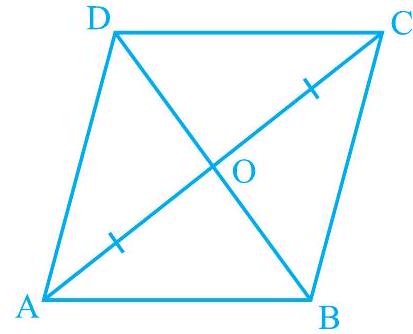
Fig. 8.7
You know that
Now, in
Therefore,
This gives,
But,
So,
or,
So, the diagonals of a rhombus are perpendicular to each other.
Example 3 :
(i)
(ii)

Fig. 8.8
Solution : (i)
So,
Also,
or,
Now, AD bisects
So,
Therefore,
(ii) Now, these equal angles form a pair of alternate angles when line segments
So,
Also,
Now, both pairs of opposite sides of quadrilateral
So,
Example 4 : Two parallel lines

Fig. 8.9
Solution : It is given that PS
The bisectors of
We are to show that quadrilateral
Now,
(Alternate angles as
So,
i.e.,
These form a pair of alternate angles for lines
So,
Similarly,
Therefore, quadrilateral
Also,
So,
or,
or,
So,
Example 5 : Show that the bisectors of angles of a parallelogram form a rectangle.
Solution : Let

Fig. 8.10
In
Since
Also,
or,
or,
So,
Similarly, it can be shown that
So, PQRS is a quadrilateral in which all angles are right angles.
Can we conclude that it is a rectangle? Let us examine. We have shown that
Therefore,
EXERCISE 8.1
1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show Answer
Solution
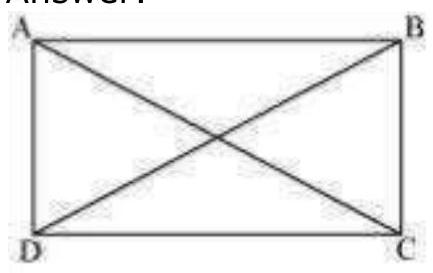
Let
In
It is known that the sum of the measures of angles on the same side of transversal is
Since
2. Show that the diagonals of a square are equal and bisect each other at right angles.
Show Answer
Solution
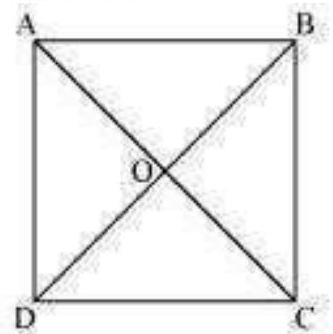
Let
In
Hence, the diagonals of a square are equal in length.
In
Hence, the diagonals of a square bisect each other.
In
As we had proved that diagonals bisect each other, therefore,
However,
Hence, the diagonals of a square bisect each other at right angles.
3. Diagonal
(i) it bisects
(ii)
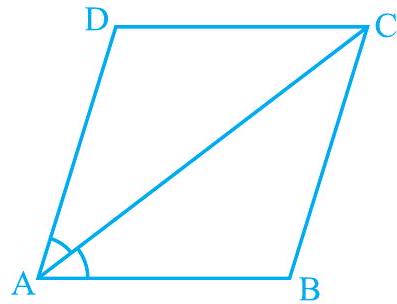
Fig. 8.11
Show Answer
Solution
(i)
And,
From equations (1), (2), and (3), we obtain
Hence,
(ii)From equation (4), we obtain
However,
is a rhombus.
4.
(i)
(ii) diagonal
Show Answer
Solution
(i) It is given that
However,
Hence,
(ii) Let us join BD.
In
However,
Also,
BD bisects b.
5. In parallelogram
(i)
(ii)
(iii)
(iv)
(v) APCQ is a parallelogram
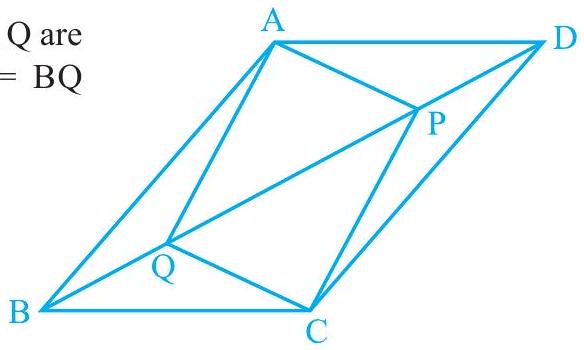
Fig. 8.12
Show Answer
Solution
(i) In
As we had observed that
(iii) In
As we had observed that
(v) From the result obtained in (ii) and (iv),
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
6.
(i)
(ii)
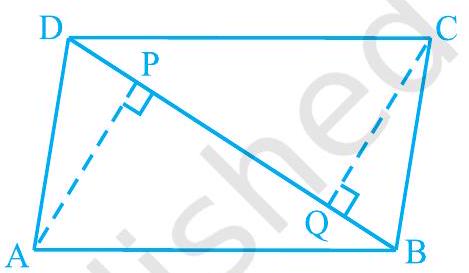
Fig. 8.13
Show Answer
Solution
(i) In
(ii) By using the above result
7.
(i)
(ii)
(iii)
(iv) diagonal
[Hint: Extend
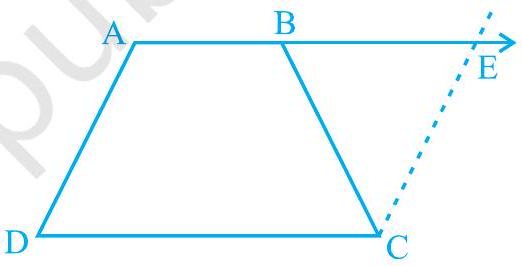
Fig. 8.14
Show Answer
Solution
Let us extend
(i)
However,
Therefore,
Consider parallel lines AD and CE. AE is the transversal line for them.
However,
From equations (1) and (2), we obtain
(ii)
Also,
However,
(iii) In
8.2 The Mid-point Theorem
You have studied many properties of a triangle as well as a quadrilateral. Now let us study yet another result which is related to the mid-point of sides of a triangle. Perform the following activity.
Draw a triangle and mark the mid-points

Fig. 8.15
Measure
What do you observe? You will find that :
so,
Repeat this activity with some more triangles.
So, you arrive at the following theorem:
Theorem 8.8 : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
You can prove this theorem using the following clue:
Observe Fig 8.16 in which

Fig. 8.16
So,
Therefore, BCDE is a parallelogram. (Why?)
This gives
In this case, also note that
Can you state the converse of Theorem 8.8? Is the converse true?
You will see that converse of the above theorem is also true which is stated as below:
Theorem 8.9 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
In Fig 8.17, observe that
Prove that

Fig. 8.17
Example 6 : In

Fig. 8.18
Solution : As D and E are mid-points of sides AB and
Similarly,
Therefore ADEF, BDFE and DFCE are all parallelograms.
Now
therefore,
Similarly
and
So, all the four triangles are congruent.
Example 7 :

Fig. 8.19
Solution : We are given that
Let us join
The trapezium ACFD is divided into two triangles;
namely
In
and
So,
Now, in
i.e.,
In other words,
EXERCISE 8.2
1.
(i)
(ii)
(iii)
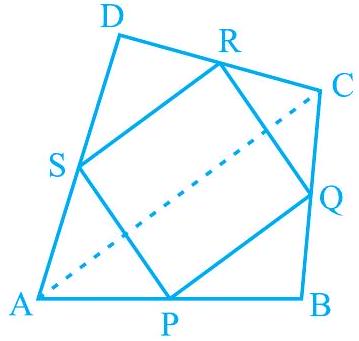
Fig. 8.20
Show Answer
Solution
(i) In
(ii) In
Using equations (1) and (2), we obtain
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal.
2.
Show Answer
Solution

b
In
AC (Using mid-point theorem) … (1)
From equations (1) and (2), we obtain
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
Let the diagonals of rhombus
In quadrilateral OMQN,
I| OM ( QR || BD)
Therefore, OMQN is a parallelogram.
However,
Clearly, PQRS is a parallelogram having one of its interior angles as
Hence,
3.
Show Answer
Solution

Let us join
In
Clearly,
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
In
However, the diagonals of a rectangle are equal. /
By using equation (1), (2), (3), (4), and (5), we obtain PQ
4.
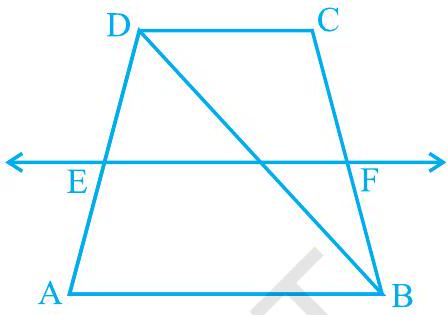
Fig. 8.21
Show Answer
Solution
Let

By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side.
In
Therefore,
As
In
5. In a parallelogram

Fig. 8.22
Show Answer
Solution
And hence, AE I| FC
Again,
In quadrilateral
In
DQ.
Similarly, in
Therefore, by using the converse of mid-point theorem, it can be said that
From equations (1) and (2), DP
Hence, the line segments
6.
(i) D is the mid-point of AC
(ii)
(iii)
Show Answer
Solution

(i) In
It is given that
Therefore,
(ii) As DM ||
(iii) Join MC.
In
Therefore,

congruence rule)
However,
Therefore, it fan be said that
8.3 Summary
In this chapter, you have studied the following points :
1. A diagonal of a parallelogram divides it into two congruent triangles.
2. In a parallelogram,
(i) opposite sides are equal
(ii) opposite angles are equal
(iii) diagonals bisect each other
3. Diagonals of a rectangle bisect each other and are equal and vice-versa.
4. Diagonals of a rhombus bisect each other at right angles and vice-versa.
5. Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
6. The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.
7. A line through the mid-point of a side of a triangle parallel to another side bisects the third side.










