अध्याय 08 चतुर्भुज
8.1 समांतर चतुर्भुज के गुण
आप कक्षा आठ में चतुर्भुजों और उनके प्रकारों का अध्ययन कर चुके हैं। एक चतुर्भुज चार भुजाएँ, चार कोण और चार शीर्ष हैं। एक समांतर चतुर्भुज एक चतुर्भुज है जिसमें सम्मुख भुजाओं के दोनों युग्म समांतर हैं आइए एक क्रियाकलाप करें।
कागज पर एक समांतर चतुर्भुज खींच कर उसे काट लीजिए। अब इसे विकर्ण के अनुदिश काट लीजिए (देखिए आकृति 8.1)। आप दो त्रिभुज प्राप्त करते हैं। इन त्रिभुजों के बारे में आप क्या कह सकते हैं?
एक त्रिभुज को दूसरे त्रिभुज पर रखिए। यदि आवश्यक हो, तो त्रिभुज को घुमाइए भी। आप क्या देखते हैं?
देखिए कि दोनों त्रिभुज परस्पर सर्वांगसम हैं।

आकृति 8.1
कुछ और समांतर चतुर्भुज खींच कर इस क्रियाकलाप को दोहराइए। प्रत्येक बार आप पाएँगे कि समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है। अब आइए इस परिणाम को सिद्ध करें।
प्रमेय 8.1 : किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
उपपत्ति : मान लीजिए

आकृति 8.2
इसलिए,
साथ ही,
इसलिए,
और
अतः,
अर्थात् विकर्ण
अब समांतर चतुर्भुज
आप पाएँगे कि
यह समांतर चतुर्भुज का एक अन्य गुण है, जिसे नीचे दिया जा रहा है :
प्रमेय 8.2 : एक समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती हैं।
आप पहले ही सिद्ध कर चुके हैं कि समांतर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है। अतः, आप इनके संगत भागों, मान लीजिए भुजाओं, के बारे में क्या कह सकते हैं? ये बराबर हैं।
इसलिए,
अब इस परिणाम का विलोम क्या है? आप जानते हैं कि जो प्रमेय (किसी कथन) में दिया हो, तो उसके विलोम में उसे सिद्ध करना होता है और जो प्रमेय में दिया गया है उसे विलोम में दिया हुआ माना जाता है। ध्यान दीजिए कि प्रमेय 8.2 को निम्न रूप में भी लिखा जा सकता है :
यदि एक चतुर्भुज एक समांतर चतुर्भुज है, तो उसकी सम्मुख भुजाओं का प्रत्येक युग्म बराबर होता है। इसलिए, इसका विलोम निम्न होगा :
प्रमेय 8.3 : यदि एक चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है।
क्या आप इसके कारण दे सकते हैं?
मान लीजिए चतुर्भुज

आकृति 8.3
स्पष्टतः,
( क्यों?) अतः,
और
क्या अब आप कह सकते हैं कि
आपने अभी देखा है कि एक समांतर चतुर्भुज में सम्मुख भुजाओं का प्रत्येक युग्म बराबर होता है और विलोमतः यदि किसी चतुर्भुज में सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है। क्या हम यही परिणाम सम्मुख कोणों के युग्मों के बारे में भी निकाल सकते हैं?
एक समांतर चतुर्भुज खींचिए और उसके कोणों को मापिए। आप क्या देखते हैं?
सम्मुख कोणों का प्रत्येक युग्म बराबर है।
इसे कुछ और समांतर चतुर्भुज लेकर दोहराइए। इससे हम एक अन्य परिणाम पर पहुँचते हैं, जो निम्न है :
प्रमेय 8.4 : एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
अब, क्या इस परिणाम का विलोम भी सत्य है? हाँ, ऐसा ही है। चतुर्भुज के कोण योग गुण और तिर्यक रेखा द्वारा प्रतिच्छेदित समांतर रेखाओं के गुणों का प्रयोग करके, हम देख सकते हैं कि उपरोक्त का विलोम भी सत्य है। इस प्रकार, हमें निम्न प्रमेय प्राप्त होती है:
प्रमेय 8.5 : यदि एक चतुर्भुज में सम्मुख कोणों का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है।
समांतर चतुर्भुज का एक गुण और भी है। आइए इसका अध्ययन करें। एक समांतर चतुर्भुज

आकृति 8.4
आप क्या देखते हैं? आप देखेंगे कि
है। अर्थात्
कुछ और समांतर चतुर्भुज लेकर इस क्रियाकलाप को दोहराइए।
प्रत्येक बार, आप प्राप्त करेंगे कि
इस प्रकार, हम निम्न प्रमेय प्राप्त करते हैं :
प्रमेय 8.6 : समांतर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाजित करते हैं।
अब, यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो क्या होगा? क्या यह एक समांतर चतुर्भुज होगा? वास्तव में, यह सत्य है।
यह प्रमेय 8.6 के परिणाम का विलोम है। इसे नीचे दिया जा रहा है :
प्रमेय 8.7 : यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो वह एक समांतर चतुर्भुज होता है।
आप इस परिणाम के लिए तर्क निम्न प्रकार दे सकते हैं :
ध्यान दीजिए कि आकृति 8.5 में, यह दिया है कि

आकृति 8.5
अत:,
इसलिए,
इससे हमें
इसी प्रकार,
अतः,
आइए अब कुछ उदाहरण लें।
उदाहरण 1 : दर्शाइए कि एक आयत का प्रत्येक कोण एक समकोण होता है।
हल : याद कीजिए कि एक आयत क्या होता है।
एक आयत वह समांतर चतुर्भुज होता है जिसका एक कोण समकोण हो।
मान लीजिए
हमें दर्शाना है कि

आकृति 8.6
इसलिए,
परन्तु,
इसलिए,
अब
(समांतर चतुर्भुज के सम्मुख कोण)
इसलिए,
अतः, आयत का प्रत्येक कोण
उदाहरण 2 : दर्शाइए कि एक समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।
हल : समचतुर्भुज 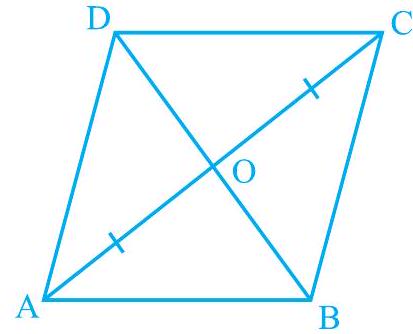
आकृति 8.7
आप जानते हैं कि
अब,
अतः,
इसलिए,
परन्तु,
इसलिए,
या,
अतः, समचर्तुभुज के विकर्ण परस्पर लम्ब हैं।
उदाहरण 3 :
(i)
(ii)

आकृति 8.8
हल : (i)
इसलिए,
साथ ही,
या,
अब,
इसलिए,
अतः,
(ii) अब ये दोनों बराबर कोण वे एकांतर कोण हैं जो रेखाखंडों
इसलिए,
साथ ही,
इस प्रकार, चतुर्भुज
अतः,
उदाहरण 4 : दो समांतर रेखाओं

आकृति 8.9
हल : यह दिया है कि
हमें दर्शाना है कि चतुर्भुज
अब,
(
इसलिए,
अर्थात्,
ये बराबर कोण रेखाओं
इसलिए,
इसी प्रकार,
अतः,
साथ ही,
इसलिए,
या,
या,
इसलिए,
उदाहरण 5 : दर्शाइए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत बनाते हैं।
हल : मान लीजिए

आकृति 8.10
चूँकि DS कोण D को और AS कोण A को समद्विभाजित करते हैं, इसलिए
साथ ही,
या,
या,
अतः,
इसी प्रकार, यह दर्शाया जा सकता है कि
इसलिए,
क्या हम निष्कर्ष निकाल सकते हैं कि यह एक आयत है? आइए इसकी जाँच करें।
हम दर्शा चुके हैं कि
अतः
प्रश्नावली 8.1
1. यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
Show Answer
Missing2. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
Show Answer
Missing3. समांतर चतुर्भुज
(i) यह
(ii)
आकृति 8.11
Show Answer
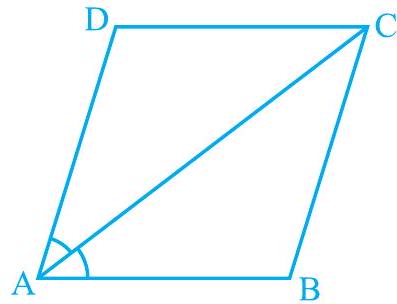
Missing4.
(i)
(ii) विकर्ण
Show Answer
Missing5. समांतर चतुर्भुज
(i)
(ii)
(iii)
(iv)
(v) APCQ एक समांतर चतुर्भुज है।
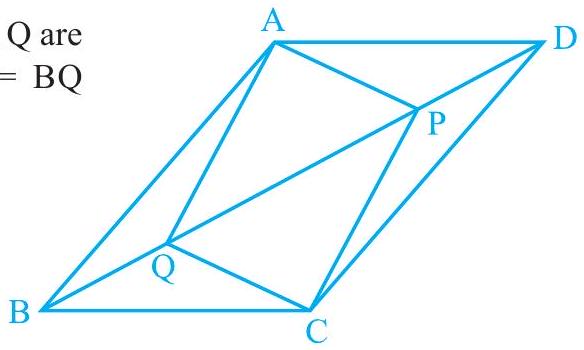
आकृति 8.12
Show Answer
Missing6.
(i)
(ii)
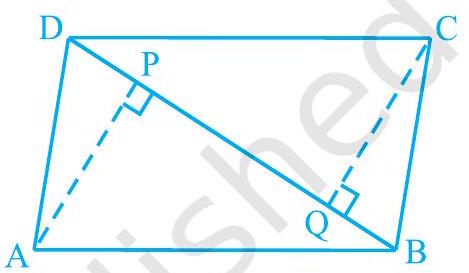
आकृति 8.13
Show Answer
Missing7.
(i)
(ii)
(iii)
(iv) विकर्ण
[संकेत :
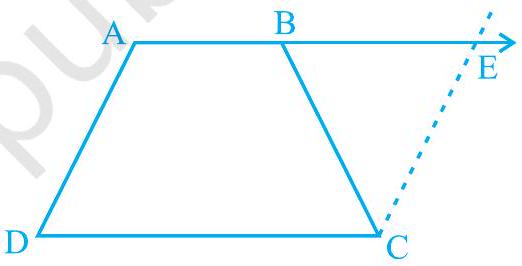
आकृति 8.14
Show Answer
Missing8.2 मध्य-बिंदु प्रमेय
आप एक त्रिभुज और एक चतुर्भुज के अनेक गुणों का अध्ययन कर चुके हैं। आइए त्रिभुज के एक अन्य गुण का अध्ययन करें, जो एक त्रिभुज की भुजाओं के मध्य-बिंदुओं से संबंधित है। इसके लिए, निम्नलिखित क्रियाकलाप कीजिए :
एक त्रिभुज

आकृति 8.15
आप क्या देखते हैं? आप पाएँगे कि
है। अतः,
कुछ अन्य त्रिभुज लेकर, इस क्रियाकलाप को दोहराइए।
इस प्रकार, आप सरलता से निम्न प्रमेय पर पहुँच सकते हैं:
प्रमेय 8.8 : किसी त्रिभुज की किन्ही दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।
आप इस प्रमेय को निम्नलिखित संकेत की सहायता से सिद्ध कर सकते हैं।
आकृति 8.16 को देखिए, जिसमें

आकृति 8.16
इसलिए,
अतः, BCDE एक समांतर चतुर्भुज है। (क्यों?) इससे
ध्यान दीजिए कि
क्या आप प्रमेय 8.8 का विलोम लिख सकते हैं? क्या यह विलोम सत्य है?
आप देखेंगे कि ऊपर दिए गए प्रमेय का विलोम भी सत्य है। इसे नीचे दिया जा रहा है :
प्रमेय 8.9 : किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
आकृति 8.17 में देखिए कि भुजा

आकृति 8.17
उदाहरण 6 :

आकृति 8.18
हल : चूँकि
इसी प्रकार,
इसलिए,
अब,
इसलिए,
इसी प्रकार,
और
अतः, चारों त्रिभुज सर्वांगसम हैं।
उदाहरण 7 :

आकृति 8.19
हल : हमें
आइए
समलंब ACFD दो त्रिभुजों
साथ ही,
अत:,
अब,
अर्थात्
दूसरे शब्दों में,
प्रश्नावली 8.2
1.
(i)
(ii)
(iii)
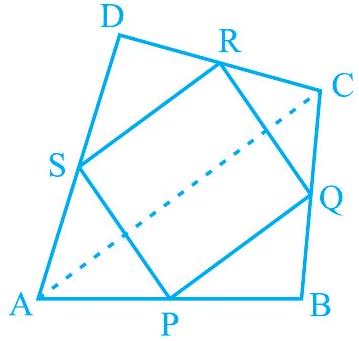
आकृति 8.20
Show Answer
Missing2.
Show Answer
Missing3.
Show Answer
Missing4.
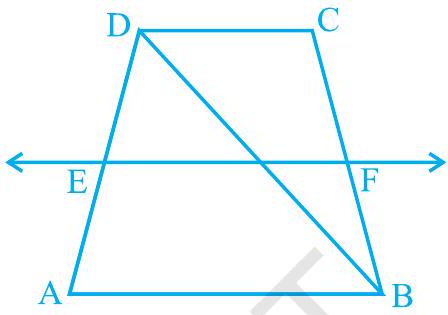
आकृति 8.21
Show Answer
Missing5. एक समांतर चतुर्भुज

आकृति 8.22
Show Answer
Missing6.
(i)
(ii)
(iii)
Show Answer
Missing8.3 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :
1. समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
2. एक समांतर चतुर्भुज में,
(i) सम्मुख भुजाएँ बराबर होती हैं।
(ii) सम्मुख कोण बराबर होते हैं।
(iii) विकर्ण परस्पर समद्विभाजित करते हैं।
3. आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
4. समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इसका विलोम भी सत्य है।
5. वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
6. किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है और उसका आधा होता है।
7. किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।










