10.1 INTRODUCTION

We have already come across simple algebraic expressions like $x+3,y-5,4x+5$, $10y-5$ and so on. In Class VI, we have seen how these expressions are useful in formulating puzzles and problems. We have also seen examples of several expressions in the chapter on simple equations.

Expressions are a central concept in algebra. This Chapter is devoted to algebraic expressions. When you have studied this Chapter, you will know how algebraic expressions are formed, how they can be combined, how we can find their values and how they can be used.

10.2 HOW ARE EXPRESSIONS FORMED?

We now know very well what a variable is. We use letters $x,y,l,m,\dots$ etc. to denote variables. A variable can take various values. Its value is not fixed. On the other hand, a constant has a fixed value. Examples of constants are: 4, 100,-17, etc.

We combine variables and constants to make algebraic expressions. For this, we use the operations of addition, subtraction, multiplication and division. We have already come across expressions like $4x+5,10y-20$. The expression $4x+5$ is obtained from the variable $x$, first by multiplying $x$ by the constant 4 and then adding the constant 5 to the product. Similarly, $10y-20$ is obtained by first multiplying $y$ by 10 and then subtracting 20 from the product.

The above expressions were obtained by combining variables with constants. We can also obtain expressions by combining variables with themselves or with other variables.

Look at how the following expressions are obtained:

$x^2,2y^2,3x^2-5,xy,4xy+7$

(i) The expression $x^2$ is obtained by multiplying the variable $x$ by itself;

$x\times x=x^2$

Just as $4\times 4$ is written as $4^2$, we write $x\times x=x^2$. It is commonly read as $x$ squared.

(Later, when you study the chapter ‘Exponents and Powers’ you will realise that $x^2$ may also be read as $x$ raised to the power 2).

In the same manner, we can write $x\times x\times x=x^3$

Commonly, $x^3$ is read as ’ $x$ cubed’. Later, you will realise that $x^3$ may also be read as $x$ raised to the power 3 .

$x,x^2,x^3,\dots$ are all algebraic expressions obtained from $x$.

(ii) The expression $2y^2$ is obtained from $y:2y^2=2\times y\times y$

Here by multiplying $y$ with $y$ we obtain $y^2$ and then we multiply $y^2$ by the constant 2 .

(iii) In $(3x^2-5)$ we first obtain $x^2$, and multiply it by 3 to get $3x^2$.

From $3x^2$, we subtract 5 to finally arrive at $3x^2-5$.

(iv) In $xy$, we multiply the variable $x$ with another variable $y$. Thus, $x\times y=xy$.

(v) In $4xy+7$, we first obtain $xy$, multiply it by 4 to get $4xy$ and add 7 to $4xy$ to get the expression.

TRY THESE

Describe how the following expressions are obtained:

$7xy+5,x^{2}y,4x^2-5x$

10.3 TERMS OF AN EXPRESSION

We shall now put in a systematic form what we have learnt above about how expressions are formed. For this purpose, we need to understand what terms of an expression and their factors are.

Consider the expression $(4x+5)$. In forming this expression, we first formed $4x$ separately as a product of 4 and $x$ and then added 5 to it. Similarly consider the expression $(3x^2+7y)$. Here we first formed $3x^2$ separately as a product of $3,x$ and $x$. We then formed $7y$ separately as a product of 7 and $y$. Having formed $3x^2$ and $7y$ separately, we added them to get the expression.

You will find that the expressions we deal with can always be seen this way. They have parts which are formed separately and then added. Such parts of an expression which are formed separately first and then added are known as terms. Look at the expression $(4x^2-3xy)$. We say that it has two terms, $4x^2$ and $-3xy$. The term $4x^2$ is a product of 4, $x$ and $x$, and the term (-3xy) is a product of (-3), $x$ and $y$.

Terms are added to form expressions. Just as the terms $4x$ and 5 are added to form the expression $(4x+5)$, the terms $4x^2$ and ( $.-3xy)$ are added to give the expression $(4x^2-3xy)$. This is because $4x^2+(-3xy)=4x^2-3xy$.

Note, the minus sign (-) is included in the term. In the expression $4x^2-3xy$, we took the term as $(-3xy)$ and not as (3xy). That is why we do not need to say that terms are ‘added or subtracted’ to form an expression; just ‘added’ is enough.

Factors of a term

We saw above that the expression $(4x^2-3xy)$ consists of two terms $4x^2$ and $-3xy$. The term $4x^2$ is a product of 4, $x$ and $x$; we say that 4, $x$ and $x$ are the factors of the term $4x^2$. A term is a product of its factors. The term $-3xy$ is a product of the factors $-3,x$ and $y$.

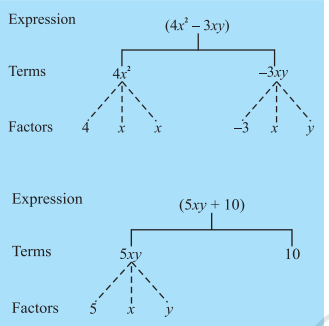
We can represent the terms and factors of the terms of an expression conveniently and elegantly by a tree diagram. The tree for the expression $(4x^2-3xy)$ is as shown in the adjacent figure.

Note, in the tree diagram, we have used dotted lines for factors and continuous lines for terms. This is to avoid mixing them.

Let us draw a tree diagram for the expression $5xy+10$.

The factors are such that they cannot be further factorised. Thus we do not write $5xy$ as $5\times xy$, because $xy$ can be further factorised. Similarly, if $x^3$ were a term, it would be written as $x\times x\times x$ and not $x^2\times x$. Also, remember that 1 is not taken as a separate factor.

TRY THESE

1. What are the terms in the following expressions?

Show how the terms are formed. Draw a tree diagram for each expression:

$8y+3x^2,7mn-4,2x^{2}y$.

2. Write three expression each having 4 terms.

Coefficients

We have learnt how to write a term as a product of factors. One of these factors may be numerical and the others algebraic (i.e., they contain variables). The numerical factor is said to be the numerical coefficient or simply the coefficient of the term. It is also said to be the coefficient of the rest of the term (which is obviously the product of algebraic factors of the term). Thus in $5xy,5$ is the coefficient of the term. It is also the coefficient of $xy$. In the term $10xyz,10$ is the coefficient of $xyz$, in the term $-7x^2{y}^2,-7$ is the coefficient of $x^2{y}^2$.

When the coefficient of a term is +1 , it is usually omitted. For example, $1x$ is written as $x;1x^2{y}^2$ is written as $x^2{y}^2$ and so on. Also, the coefficient ( -1 ) is indicated only by the minus sign. Thus $(-1)x$ is written as $-x;(-1)x^2{y}^2$ is written as $-x^2{y}^2$ and so on.

TRY THESE

Identify the coefficients of the terms of following expressions:

$4x-3y,a+b+5,2y+5,2xy$

Sometimes, the word ‘coefficient’ is used in a more general way. Thus we say that in the term $5xy,5$ is the coefficient of $xy,x$ is the coefficient of $5y$ and $y$ is the coefficient of $5x$. In $10x{y}^2,10$ is the coefficient of $x{y}^2,x$ is the coefficient of $10y^2$ and $y^2$ is the coefficient of $10x$. Thus, in this more general way, a coefficient may be either a numerical factor or an algebraic factor or a product of two or more factors. It is said to be the coefficient of the product of the remaining factors.

Example 1 Identify, in the following expressions, terms which are not constants. Give their numerical coefficients:

$xy+4,13-y^2,13-y+5y^2,4p^{2}q-3p{q}^2+5$

Solution

Example 2

(a) What are the coefficients of $x$ in the following expressions?

$4x-3y,8-x+y,y^{2}x-y,2z-5xz$

(b) What are the coefficients of $y$ in the following expressions?

$4x-3y,8+yz,y{z}^2+5,my+m$

Solution

(a) In each expression we look for a term with $x$ as a factor. The remaining part of that term is the coefficient of $x$.

(b) The method is similar to that in (a) above.

10.4 LIKE AND UNLIKE TERMS

When terms have the same algebraic factors, they are like terms. When terms have different algebraic factors, they are unlike terms. For example, in the expression $2xy-3x+5xy-4$, look at the terms $2xy$ and $5xy$. The factors of $2xy$ are 2, $x$ and $y$. The factors of $5xy$ are 5, $x$ and $y$. Thus their algebraic (i.e., those which contain variables) factors are the same and

TRY THESE

Group the like terms together from the following:

$12x,12,-25x,-25,-25y,1,x,12y,y$ hence they are like terms. On the other hand the terms $2xy$ and $-3x$, have different algebraic factors. They are unlike terms. Similarly, the terms, $2xy$ and 4, are unlike terms. Also, the terms $-3x$ and 4 are unlike terms.

10.5 MONOMIALS, BINOMIALS, TRINOMIALS AND POLYNOMIALS

An expression with only one term is called a monomial; for example, $7xy,-5m$, $3z^2,4$ etc.

TRY THESE

Classify the following expressions as a monomial, a binomial or a trinomial: $a$, $a+b,ab+a+b,ab+a$ $+b-5,xy,xy+5$, $5x^2-x+2,4pq-3q+5p$, $7,4m-7n+10,4mn+7$.

An expression which contains two unlike terms is called a binomial; for example, $x+y,m-5,mn+4m,a^2-b^2$ are binomials. The expression $10pq$ is not a binomial; it is a monomial. The expression $(a+b+5)$ is not a binomial. It contains three terms.

An expression which contains three terms is called a trinomial; for example, the expressions $x+y+7,ab+a+b$, $3x^2-5x+2,m+n+10$ are trinomials. The expression $ab+a+b+5$ is, however not a trinomial; it contains four terms and not three. The expression $x+y+5x$ is not a trinomial as the terms $x$ and $5x$ are like terms.

In general, an expression with one or more terms is called a polynomial. Thus a monomial, a binomial and a trinomial are all polynomials.

Example 3 State with reasons, which of the following pairs of terms are of like terms and which are of unlike terms:

(i) $7x,12y$

(ii) $15x,-21x$

(iii) $-4ab,7ba$

(iv) $3xy,3x$

(v) $6x{y}^2,9x^{2}y$

(vi) $p{q}^2,-4p{q}^2$

(vii) $m{n}^2,10mn$

Solution

Following simple steps will help you to decide whether the given terms are like or unlike terms:

(i) Ignore the numerical coefficients. Concentrate on the algebraic part of the terms.

(ii) Check the variables in the terms. They must be the same.

(iii) Next, check the powers of each variable in the terms. They must be the same.

Note that in deciding like terms, two things do not matter (1) the numerical coefficients of the terms and (2) the order in which the variables are multiplied in the terms.

EXERCISE 10.1

1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

(i) Subtraction of $z$ from $y$.

(ii) One-half of the sum of numbers $x$ and $y$.

(iii) The number $z$ multiplied by itself.

(iv) One-fourth of the product of numbers $p$ and $q$.

(v) Numbers $x$ and $y$ both squared and added.

(vi) Number 5 added to three times the product of numbers $m$ and $n$.

(vii) Product of numbers $y$ and $z$ subtracted from 10.

(viii) Sum of numbers $a$ and $b$ subtracted from their product.

2. (i) Identify the terms and their factors in the following expressions Show the terms and factors by tree diagrams.

(a) $x-3$

(b) $1+x+x^2$

(c) $y-y^3$

(d) $5x{y}^2+7x^{2}y$

(e) $-ab+2b^2-3a^2$

(ii) Identify terms and factors in the expressions given below:

(a) $-4x+5$

(b) $-4x+5y$

(c) $5y+3y^2$

(d) $xy+2x^2{y}^2$

(e) $pq+q$

(f) $1.2ab-2.4b+3.6a$

(g) $\frac{3}{4}x+\frac{1}{4}$

(h) $0.1p^2+0.2q^2$

3. Identify the numerical coefficients of terms (other than constants) in the following expressions:

(i) $5-3t^2$

(ii) $1+t+t^2+t^3$

(iii) $x+2xy+3y$

(iv) $100m+1000n$

(v) $-p^2{q}^2+7pq$

(vi) $1.2a+0.8b$

(vii) $3.14r^2$

(viii) $2(l+b)$

(ix) $0.1y+0.01y^2$

4. (a) Identify terms which contain $x$ and give the coefficient of $x$.

(i) $y^{2}x+y$

(ii) $13y^2-8yx$

(iii) $x+y+2$

(iv) $5+z+zx$

(v) $1+x+xy$

(vi) $12x{y}^2+25$

(vii) $7x+x{y}^2$

(b) Identify terms which contain $y^2$ and give the coefficient of $y^2$.

(i) $8-x{y}^2$

(ii) $5y^2+7x$

(iii) $2x^{2}y-15x{y}^2+7y^2$

5. Classify into monomials, binomials and trinomials.

(i) $4y-7z$

(ii) $y^2$

(iii) $x+y-xy$

(iv) 100

(v) $ab-a-b$

(vi) $5-3t$

(vii) $4p^{2}q-4p{q}^2$

(viii) $7mn$

(ix) $z^2-3z+8$

(x) $a^2+b^2$

(xi) $z^2+z$

(xii) $1+x+x^2$

6. State whether a given pair of terms is of like or unlike terms.

(i) 1,100

(ii) $-7x,\frac{5}{2}x$

(iii) $-29x,-29y$

(iv) $14xy,42yx$

(v) $4m^{2}p,4m{p}^2$

(vi) $12xz,12x^2{z}^2$

7. Identify like terms in the following:

(a) $-x{y}^2,-4y{x}^2,8x^2,2x{y}^2,7y,-11x^2,-100x,-11yx,20x^{2}y$, $-6x^2,y,2xy,3x$

(b) $10pq,7p,8q,-p^2{q}^2,-7qp,-100q,-23,12q^2{p}^2,-5p^2,41,2405p,78qp$, $13p^{2}q,q{p}^2,701p^2$

10.6 FINDING THE VALUE OF AN EXPRESSION

We know that the value of an algebraic expression depends on the values of the variables forming the expression. There are a number of situations in which we need to find the value of an expression, such as when we wish to check whether a particular value of a variable satisfies a given equation or not.

We find values of expressions, also, when we use formulas from geometry and from everyday mathematics. For example, the area of a square is $l^2$, where $l$ is the length of a side of the square. If $l=5cm$., the area is $5^{2}c{m}^2$ or $25c{m}^2$; if the side is $10cm$, the area is ${10}^{2}c{m}^2$ or $100c{m}^2$ and so on. We shall see more such examples in the next section.

Example 4 Find the values of the following expressions for $x=2$.

(i) $x+4$

(ii) $4x-3$

(iii) $19-5x^2$

(iv) $100-10x^3$

Solution

Putting $x=2$

(i) In $x+4$, we get the value of $x+4$, i.e.,

$x+4=2+4=6$

(ii) In $4x-3$, we get

$4x-3=(4\times 2)-3=8-3=5$

(iii) In $19-5x^2$, we get

$19-5x^2=19-(5\times 2^2)=19-(5\times 4)=19-20=-1$

(iv) In $100-10x^3$, we get

$\begin{array}{rl}& 100-10x^3=100-(10\times 2^3)=100-(10\times 8)(\text{ Note }{2}^3=8)\\ & =100-80=20\end{array}$

Example 5 Find the value of the following expressions when $n=-2$.

(i) $5n-2$

(ii) $5n^2+5n-2$

(iii) $n^3+5n^2+5n-2$

Solution

(i) Putting the value of $n=-2$, in $5n-2$, we get,

$5(-2)-2=-10-2=-12$

(ii) In $5n^2+5n-2$, we have,

for $n=-2,5n-2=-12$

and $5n^2=5\times (-2{)}^2=5\times 4=20$ [as $.(-2{)}^2=4]$

Combining,

$5n^2+5n-2=20-12=8$

(iii) Now, for $n=-2$,

$\begin{array}{rl}& 5n^2+5n-2=8\text{ and }\\ & n^3=(-2{)}^3=(-2)\times (-2)\times (-2)=-8\end{array}$

Combining,

$n^3+5n^2+5n-2=-8+8=0$

We shall now consider expressions of two variables, for example, $x+y,xy$. To work out the numerical value of an expression of two variables, we need to give the values of both variables. For example, the value of $(x+y)$, for $x=3$ and $y=5$, is $3+5=8$.

Example 6 Find the value of the following expressions for $a=3,b=2$.

(i) $a+b$

(ii) $7a-4b$

(iii) $a^2+2ab+b^2$

(iv) $a^3-b^3$

Solution

Substituting $a=3$ and $b=2$ in

(i) $a+b$, we get

$a+b=3+2=5$

(ii) $7a-4b$, we get

$7a-4b=7\times 3-4\times 2=21-8=13$.

(iii) $a^2+2ab+b^2$, we get

$a^2+2ab+b^2=3^2+2\times 3\times 2+2^2=9+2\times 6+4=9+12+4=25$

(iv) $a^3-b^3$, we get

$a^3-b^3=3^3-2^3=3\times 3\times 3-2\times 2\times 2=9\times 3-4\times 2=27-8=19$

EXERCISE 10.2

1. If $m=2$, find the value of:

(i) $m-2$

(ii) $3m-5$

(iii) $9-5m$

(iv) $3m^2-2m-7$

(v) $\frac{5m}{2}4$

2. If $p=-2$, find the value of:

(i) $4p+7$

(ii) $-3p^2+4p+7$

(iii) $-2p^3-3p^2+4p+7$

3. Find the value of the following expressions, when $x=-1$ :

(i) $2x-7$

(ii) $-x+2$

(iii) $x^2+2x+1$

(iv) $2x^2-x-2$

4. If $a=2,b=-2$, find the value of:

(i) $a^2+b^2$

(ii) $a^2+ab+b^2$

(iii) $a^2-b^2$

5. When $a=0,b=-1$, find the value of the given expressions:

(i) $2a+2b$

(ii) $2a^2+b^2+1$

(iii) $2a^{2}b+2a{b}^2+ab$

(iv) $a^2+ab+2$

6. Simplify the expressions and find the value if $x$ is equal to 2

(i) $x+7+4(x-5)$

(ii) $3(x+2)+5x-7$

(iii) $6x+5(x-2)$

(iv) $4(2x-1)+3x+11$

7. Simplify these expressions and find their values if $x=3,a=-1,b=-2$.

(i) $3x-5-x+9$

(ii) $2-8x+4x+4$

(iii) $3a+5-8a+1$

(iv) $10-3b-4-5b$

(v) $2a-2b-4-5+a$

8. (i) If $z=10$, find the value of $z^3-3(z-10)$.

(ii) If $p=-10$, find the value of $p^2-2p-100$

9. What should be the value of $a$ if the value of $2x^2+x-a$ equals to 5 , when $x=0$ ?

10. Simplify the expression and find its value when $a=5$ and $b=-3$.

$2(a^2+ab)+3-ab$

WHAT HAVE WE DISCUSSED?

1. Algebraic expressions are formed from variables and constants. We use the operations of addition, subtraction, multiplication and division on the variables and constants to form expressions. For example, the expression $4xy+7$ is formed from the variables $x$ and $y$ and constants 4 and 7. The constant 4 and the variables $x$ and $y$ are multiplied to give the product $4xy$ and the constant 7 is added to this product to give the expression.

2. Expressions are made up of terms. Terms are added to make an expression. For example, the addition of the terms $4xy$ and 7 gives the expression $4xy+7$.

3. A term is a product of factors. The term $4xy$ in the expression $4xy+7$ is a product of factors $x,y$ and 4 . Factors containing variables are said to be algebraic factors.

4. The coefficient is the numerical factor in the term. Sometimes anyone factor in a term is called the coefficient of the remaining part of the term.

5. Any expression with one or more terms is called a polynomial. Specifically a one term expression is called a monomial; a two-term expression is called a binomial; and a three-term expression is called a trinomial.

6. Terms which have the same algebraic factors are like terms. Terms which have different algebraic factors are unlike terms. Thus, terms $4xy$ and $-3xy$ are like terms; but terms $4xy$ and $-3x$ are not like terms.

7. In situations such as solving an equation and using a formula, we have to find the value of an expression. The value of the expression depends on the value of the variable from which the expression is formed. Thus, the value of $7x-3$ for $x=5$ is 32 , since $7(5)-3=35-3=32$.