Work Power and Energy 5 Question 6
8. A particle, which is constrained to move along
(a)
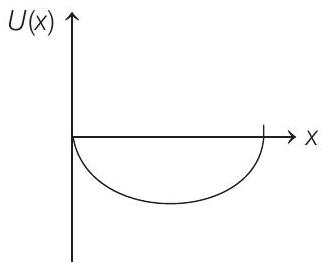
(b)
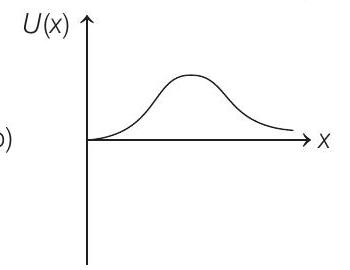
(c)
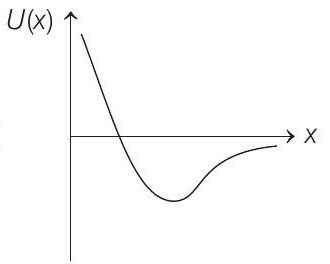
(d)
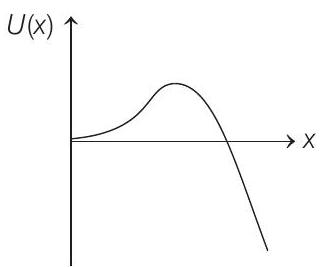
Show Answer
Answer:
Correct Answer: 8. (d)
Solution:
or
From the given function, we can see that






