Work Power and Energy 5 Question 14
17. A particle of unit mass is moving along the $x$-axis under the influence of a force and its total energy is conserved. Four possible forms of the potential energy of the particle are given in Column I ( $a$ and $U _0$ are constants). Match the potential energies in Column I to the corresponding statements in Column II
(2015 Adv.)
| Column I | Column II |
|---|---|
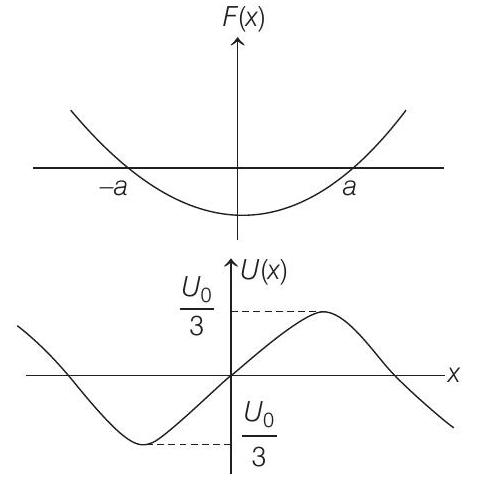
| A. $U_1(x)=\frac{U_0}{2}\left[1-\left(\frac{x}{a}\right)^2\right]^2$ | P. The force acting on the particle is zero at $x=a |
| B. $U_2(x)=\frac{U_0}{2}\left(\frac{x}{a}\right)^2$ | Q. The force acting on the particle is zero at $x=0 |
| C. $U_3(x)=\frac{U_0}{2}\left(\frac{x}{a}\right)^2 \exp \left[-\left(\frac{x}{a}\right)^2\right]$ | R. The force acting on the particle is zero at $x=-a |
| D. $U_4(x)=\frac{U_0}{2}\left[\frac{x}{a}-\frac{1}{3}\left(\frac{x}{a}\right)^3\right]$ | S. The particle experiences an attractive force towards $x=0$ in the region $ |
| T. The particle with total energy $\frac{U_0}{4}$ can oscillate about the point $x=-a$. |
Show Answer
Answer:
Correct Answer: 17. A-P, Q, R, T $\quad$ B-Q, S $\quad$ C-P, Q, R, S $\quad$ D-P, R, T
Solution:
- (A) $F _x=\frac{-d U}{d x}=-\frac{2 U _0}{a^{3}}[x-a][x][x+a]$
$$ \begin{aligned} F=0 \text { at } x=0, x=a, x=-a \\ \text { and } U=0 \text { at } x=-a \end{aligned} $$
$ \text { and } \quad x=a $
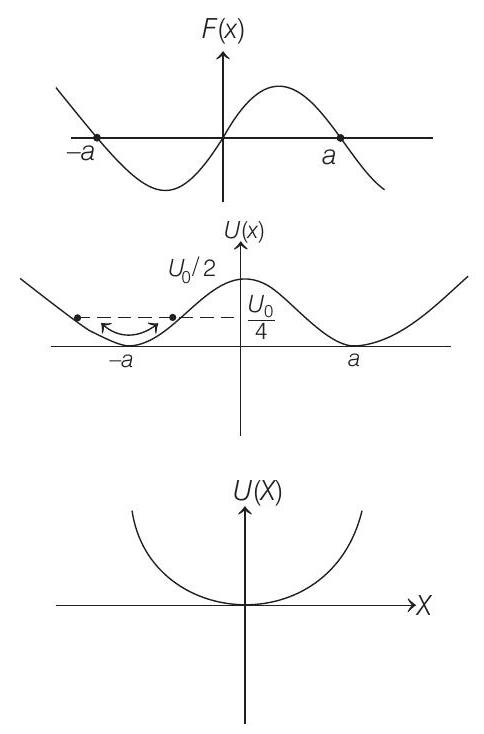
(B) $F _x=-\frac{d U}{d x}-U _0 \frac{x}{a}$
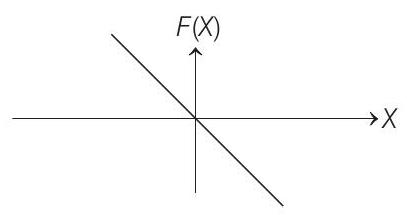
(C) $F _x=-\frac{d U}{d x}=U _0 \frac{e^{-x^{2} / x^{2}}}{a^{3}}[x][x-a][x+a]$
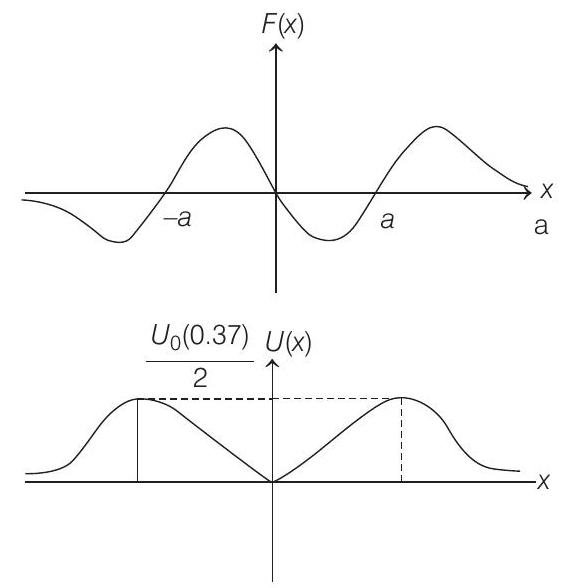
(D) $F _x=-\frac{d U}{d x}=-\frac{U _0}{2 a^{3}}[(x-a)(x+a)]$