Work Power and Energy 5 Question 14
17. A particle of unit mass is moving along the
(2015 Adv.)
| Column I | Column II |
|---|---|
| A. B. C. D. |
|
| T. The particle with total energy |
|
| point |
Show Answer
Answer:
Correct Answer: 17. A-P, Q, R, T B-Q, S
Solution:
- (A)
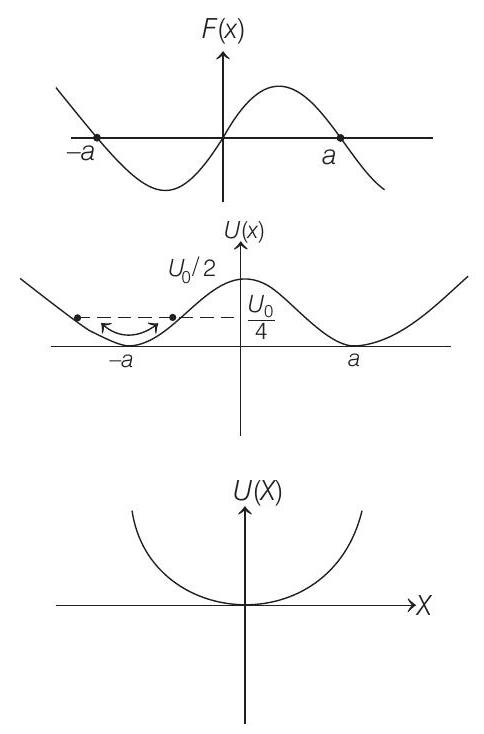
(B)
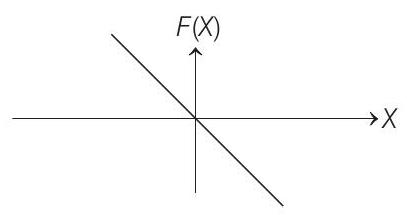
(C) 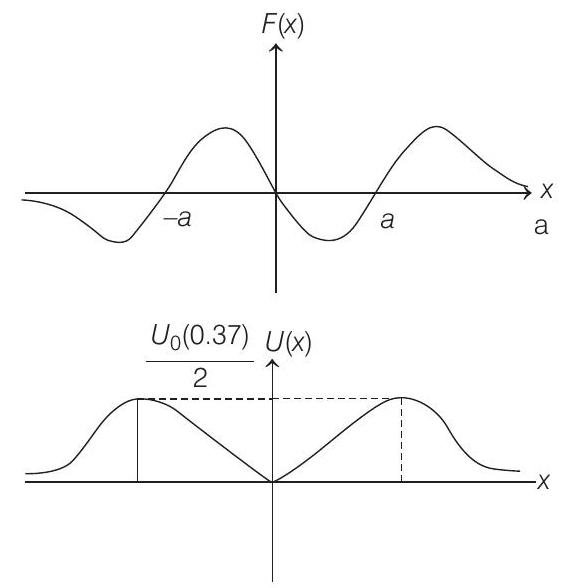
(D) 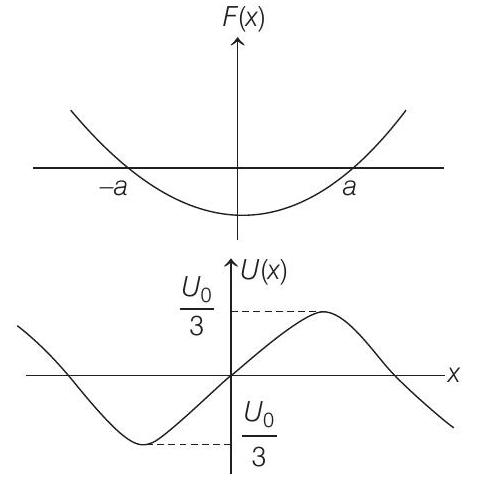
Download Chapter Test http://tinyurl.com/yyxyyt8y or






