Work Power and Energy 5 Question 12
15. A string, with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of $2 m$ from the wall, has a point mass $M=2 kg$ attached to it at a distance of $1 m$ from the wall. A mass $m=0.5 kg$ attached at the free end is held at rest so that the string is horizontal between the wall and the pulley and vertical beyond the pulley. What will be the speed with which the mass $M$ will hit the wall when the mass $m$ is released? (Take $g=9.8 m / s^{2}$ )
$(1985,6 M)$
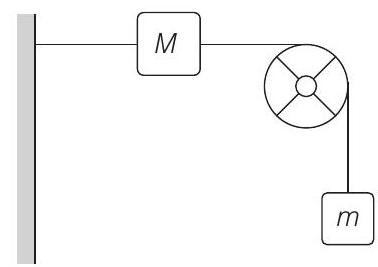
Show Answer
Answer:
Correct Answer: 15. $3.29 m / s$
Solution:
- Let $M$ strikes with speed $v$. Then, velocity of $m$ at this instant will be $v \cos \theta$ or $\frac{2}{\sqrt{5}} v$. Further $M$ will fall a distance of $1 m$ while $m$ will rise up by $(\sqrt{5}-1) m$. From energy conservation, decrease in potential energy of $M=$ increase in potential energy of $m$ +increase in kinetic energy of both the blocks.
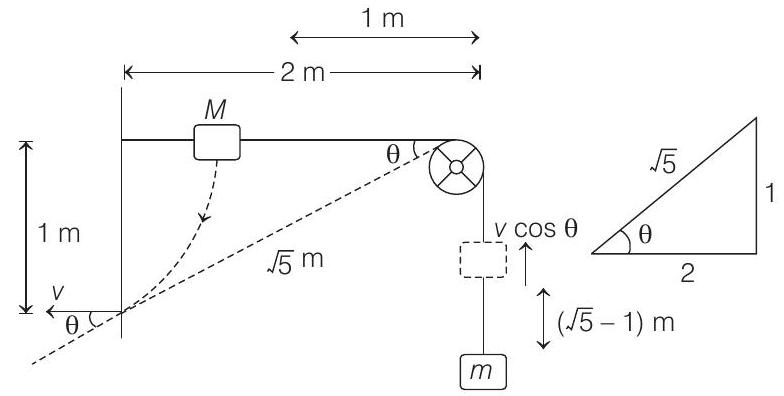
or $(2)(9.8)(1)=(0.5)(9.8)(\sqrt{5}-1)+\frac{1}{2} \times 2 \times v^{2}$
$$ +\frac{1}{2} \times 0.5 \times \frac{2 v}{\sqrt{5}}^{2} $$
Solving this equation, we get, $v=3.29 m / s$.






