Work Power and Energy 5 Question 12
15. A string, with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of
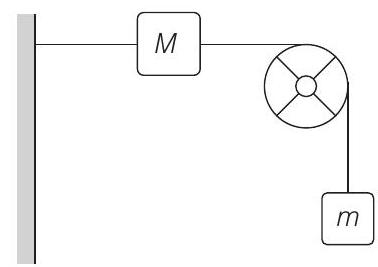
Show Answer
Answer:
Correct Answer: 15.
Solution:
- Let
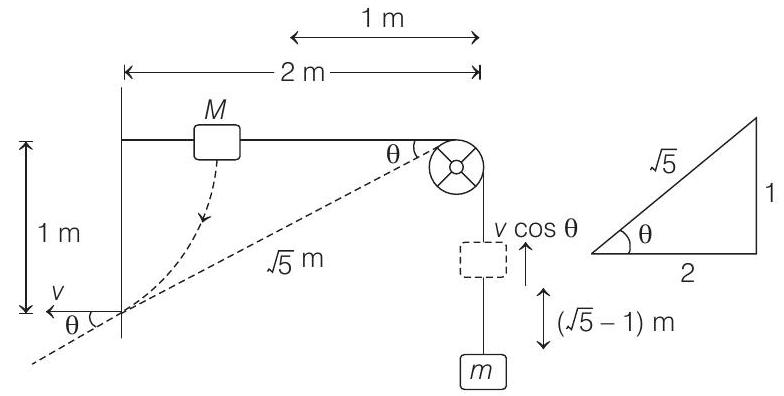
or
Solving this equation, we get,






