SATHEE: Work Power and Energy 4 Question 7

Work Power and Energy 4 Question 7

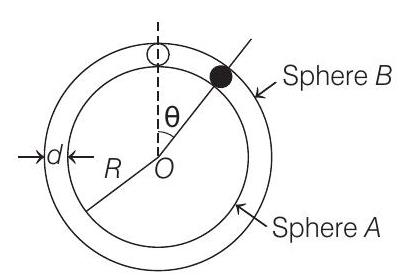9. A spherical ball of mass $m$ is kept at the highest point in the space between two fixed, concentric spheres $A$ and $B$ (see fig.). The smaller sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$ . The ball has a

diameter very slightly less than $d$ . All surfaces are frictionless. The ball is given a gentle push (towards the right in the figure). The angle made by the radius vector of the ball with the upward vertical is denoted by $θ$ .

(2002, 5M)

(a) Express the total normal reaction force exerted by the spheres on the ball as a function of angle $θ$ .

(b) Let $N_{A}$ and $N_{B}$ denote the magnitudes of the normal reaction forces on the ball exerted by the spheres $A$ and $B$ , respectively. Sketch the variations of $N_{A}$ and $N_{B}$ as function of $\cos θ$ in the range $0 \leq θ \leq π$ by drawing two separate graphs in your answer book, taking $\cos θ$ on the horizontal axis.

Show Answer

Answer:

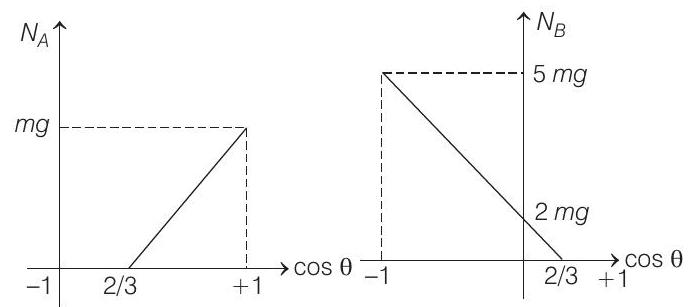
Correct Answer: 9. (a) $N = m g (3 \cos θ - 2)$

(b) For $θ \leq \cos^{- 1} \frac{2}{3}, N_{B} = 0, N_{A} = m g (3 \cos θ - 2)$ and for $θ \geq \cos^{- 1} \frac{2}{3}; N_{A} = 0, N_{B} = m g (2 - 3 \cos θ)$

Solution:

(a) $h = R + \frac{d}{2} (1 - \cos θ)$

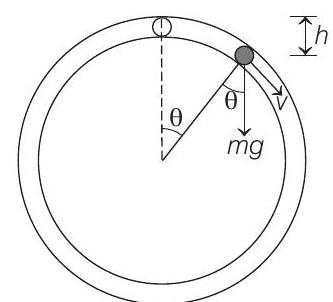
Velocity of ball at angle $θ$ is

$v^{2} = 2 g h = 2 R + \frac{d}{2} (1 - \cos θ) g$

Let $N$ be the normal reaction (away from centre) at angle $θ$ .

Then, $m g \cos θ - N = \frac{m v^{2}}{R + \frac{d}{2}}$

Substituting value of $v^{2}$ from Eq. (i), we get

$\begin{aligned} m g \cos θ - N & = 2 m g (1 - \cos θ) \\ ∴ N & = m g (3 \cos θ - 2) \end{aligned}$

(b) The ball will lose contact with the inner sphere when $N = 0$

or $3 \cos θ - 2 = 0$ or $θ = \cos^{- 1} \frac{2}{3}$

After this it makes contact with outer sphere and normal reaction starts acting towards the centre.

Thus for $θ \leq \cos^{- 1} \frac{2}{3}$

and

$\begin{aligned} N_{B} = 0 \\ N_{A} = m g (3 \cos θ - 2) \end{aligned}$

$\begin{aligned} and for \begin{array}{c} θ \geq \cos^{- 1} \frac{2}{3} \\ N_{A} = 0 and N_{B} = m g (2 - 3 \cos θ) \end{array} \end{aligned}$

The corresponding graphs are as follows.

Work Power and Energy 4 Question 7

9. A spherical ball of mass $m$ is kept at the highest point in the space between two fixed, concentric spheres $A$ and $B$ (see fig.). The smaller sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$ . The ball has a

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Work Power and Energy 4 Question 7

9. A spherical ball of mass m is kept at the highest point in the space between two fixed, concentric spheres A and B (see fig.). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

9. A spherical ball of mass $m$ is kept at the highest point in the space between two fixed, concentric spheres $A$ and $B$ (see fig.). The smaller sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$ . The ball has a