Work Power and Energy 4 Question 7
9. A spherical ball of mass $m$ is kept at the highest point in the space between two fixed, concentric spheres $A$ and $B$ (see fig.). The smaller sphere $A$ has a radius $R$ and the space between the two spheres has a width $d$. The ball has a
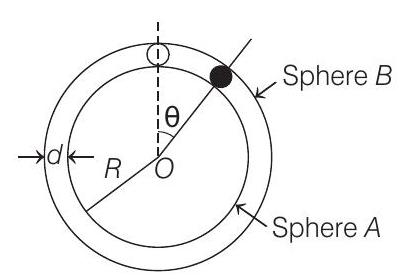diameter very slightly less than $d$. All surfaces are frictionless. The ball is given a gentle push (towards the right in the figure). The angle made by the radius vector of the ball with the upward vertical is denoted by $\theta$.
(2002, 5M)
(a) Express the total normal reaction force exerted by the spheres on the ball as a function of angle $\theta$.
(b) Let $N _A$ and $N _B$ denote the magnitudes of the normal reaction forces on the ball exerted by the spheres $A$ and $B$, respectively. Sketch the variations of $N _A$ and $N _B$ as function of $\cos \theta$ in the range $0 \leq \theta \leq \pi$ by drawing two separate graphs in your answer book, taking $\cos \theta$ on the horizontal axis.
Show Answer
Answer:
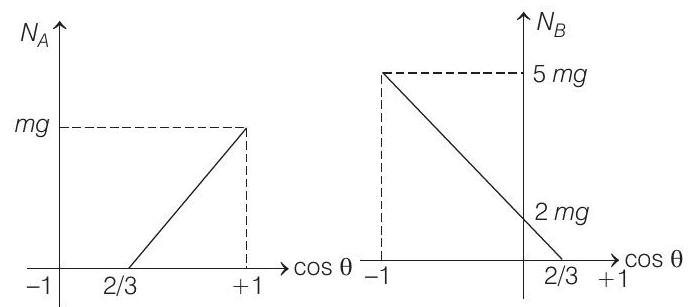
Correct Answer: 9. (a) $N=m g(3 \cos \theta-2)$
(b) For $\theta \leq \cos ^{-1} \frac{2}{3}, N _B=0, N _A=m g(3 \cos \theta-2)$ and for $\theta \geq \cos ^{-1} \frac{2}{3} ; N _A=0, N _B=m g(2-3 \cos \theta)$
Solution:
- (a) $h=R+\frac{d}{2}(1-\cos \theta)$
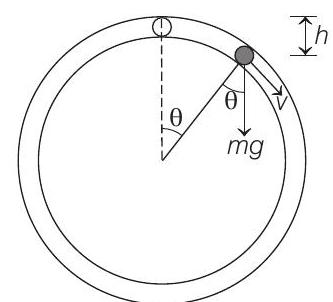
Velocity of ball at angle $\theta$ is
$$ v^{2}=2 g h=2 \quad R+\frac{d}{2}(1-\cos \theta) g $$
Let $N$ be the normal reaction (away from centre) at angle $\theta$.
Then, $m g \cos \theta-N=\frac{m v^{2}}{R+\frac{d}{2}}$
Substituting value of $v^{2}$ from Eq. (i), we get
$$ \begin{aligned} m g \cos \theta-N & =2 m g(1-\cos \theta) \\ \therefore \quad N & =m g(3 \cos \theta-2) \end{aligned} $$
(b) The ball will lose contact with the inner sphere when $N=0$
or $3 \cos \theta-2=0$ or $\theta=\cos ^{-1} \quad \frac{2}{3}$
After this it makes contact with outer sphere and normal reaction starts acting towards the centre.
Thus for $\quad \theta \leq \cos ^{-1} \frac{2}{3}$
and
$$ \begin{aligned} & N _B=0 \\ & N _A=m g(3 \cos \theta-2) \end{aligned} $$
$$ \begin{aligned} & \text { and for } \quad \begin{array}{c} \theta \geq \cos ^{-1} \frac{2}{3} \\ N _A=0 \quad \text { and } \quad N _B=m g(2-3 \cos \theta) \end{array} \end{aligned} $$
The corresponding graphs are as follows.
