SATHEE: Work Power and Energy 3 Question 1

Work Power and Energy 3 Question 1

1. A point particle of mass $m$ , moves along the uniformly rough track $P Q R$ as shown in the figure. The coefficient of friction, between the particle and the rough track equals $μ$ . The particle is released from rest, from the point $P$ and it comes to rest at a point $R$ . The energies lost by the ball, over the parts $P Q$ and $Q R$ of the track, are equal to each other, and no energy is lost when particle changes direction from $P Q$ to $Q R$ . The values of the coefficient of friction $μ$ and the distance $x$ $(= Q R)$ , are respectively close to

(2016 Main)

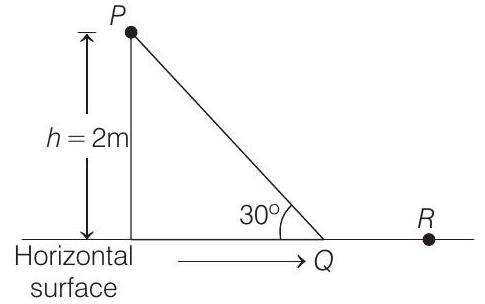
(a) 0.2 and $6.5 m$

(b) 0.2 and $3.5 m$

(d) 0.29 and $6.5 m$

The block $B$ is displaced towards wall 1 by a small distance $x$ and released. The block returns and moves a maximum distance $y$ towards wall 2. Displacements $x$ and $y$ are measured with respect to the equilibrium position of the block $B$ . The ratio $\frac{y}{x}$ is

$(2008, 3 M)$

(a) 4

(b) 2

(d) $\frac{1}{4}$

Show Answer

Answer:

Correct Answer: 1. (c)

Solution:

As energy loss is same, thus

$\begin{aligned} μ m g \cos θ \cdot (P Q) & = μ m g \cdot (Q R) \\ ∴ & Q R & = (P Q) \cos θ \\ \Rightarrow & Q R & = 4 \times \frac{\sqrt{3}}{2} \\ = 2 \sqrt{3} \approx 3.5 m \end{aligned}$

Further,decrease in potential energy $=$ loss due to friction

$∴ m g h = (μ m g \cos θ) d_{1} + (μ m g) d_{2}$

$\begin{aligned} m \times 10 \times 2 & = μ \times m \times 10 \times \frac{\sqrt{3}}{2} \times 4 \\ + μ \times m \times 10 \times 2 \sqrt{3} \\ \Rightarrow & 4 \sqrt{3} μ & = 2 μ & = \frac{1}{2 \sqrt{3}} = 0.288 = 0.29 \end{aligned}$

Work Power and Energy 3 Question 1

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Work Power and Energy 3 Question 1

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu