Work Power and Energy 1 Question 6
7. A force $\mathbf{F}=-k(y \hat{\mathbf{i}}+x \hat{\mathbf{j}})$ (where, $k$ is a positive constant) acts on a particle moving in the $x-y$ plane. Starting from the origin, the particle is taken along the positive $X$-axis to the point $(a, 0)$ and then parallel to the $Y$-axis to the point $(a, a)$. The total work done by the force $F$ on the particle is
(a) $-2 k a^{2}$
(b) $2 k a^{2}$
(c) $-k a^{2}$
(d) $k a^{2}$
(1998, 2M)
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- $d W=\mathbf{F} \cdot \mathbf{d} \mathbf{s}$, where $\mathbf{d} \mathbf{s}=d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}}+d z \hat{\mathbf{k}}$
$$ \begin{array}{rlrl} & \text { and } & \mathbf{F} & =-k(y \hat{\mathbf{i}}+x \hat{\mathbf{j}}) \\ & \therefore & d W & =-k(y d x+x d y) \\ & & =-k d(x y) \\ & & W & =\int _{0,0}^{a, a} d W=-k \int _{0,0}^{a, a} d(x y)=-k[x y] _{0,0}^{a, a} \\ & W & =-k a^{2} \end{array} $$
Alternate Answer
While moving from $(0,0)$ to $(a, 0)$ along positive $X$-axis,
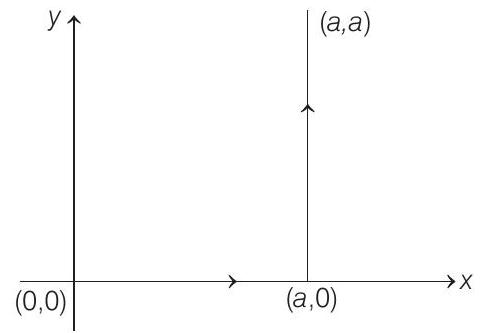
$y=0 \therefore \mathbf{F}=-k x \hat{\mathbf{j}}$ i.e. force is in negative $y$-direction while the displacement is in positive $x$-direction. Therefore, $W _1=0$ (Force $\perp$ displacement).
Then, it moves from $(a, 0)$ to $(a, a)$ along a line parallel to $Y$-axis $(x=+a)$. During this $\mathbf{F}=-k(y \hat{\mathbf{i}}+a \hat{\mathbf{j}})$
The first component of force, $-k y \hat{\mathbf{i}}$ will not contribute any work, because this component is along negative $x$-direction $(-\hat{\mathbf{i}})$ while displacement is in positive $y$-direction $(a, 0)$ to $(a, a)$.
The second component of force i.e. $-k a \hat{\mathbf{j}}$ will perform negative work $\begin{aligned} & \mathbf{F} _y=-k a \hat{\mathbf{j}} \ & \mathbf{s}=a \hat{\mathbf{j}}\end{aligned}, W _2=(-k a)(a)=-k a^{2}$
$$ \therefore \quad W=W _1+W _2=-k a^{2} $$
NOTE
In the given force, work done is path independent. It depends only on initial and final positions. Therefore, first method is brief and correct






