Wave Motion 4 Question 5
5. Two cars $A$ and $B$ are moving away from each other in opposite directions. Both the cars are moving with a speed of $20 ms^{-1}$ with respect to the ground. If an observer in car $A$ detects a frequency $2000 Hz$ of the sound coming from car $B$, what is the natural frequency of the sound source in car $B$ ? (speed of sound in air $=340 ms^{-1}$ )
(2019 Main, 9 April II)
(a) $2060 Hz$
(b) $2250 Hz$
(c) $2300 Hz$
(d) $2150 Hz$
Show Answer
Solution:
- The given condition can be shown below as,
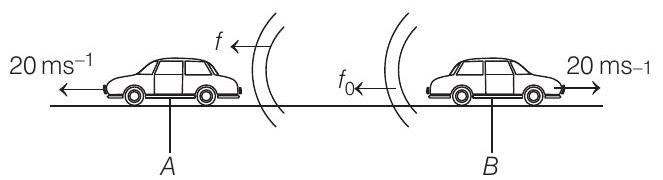
Here, source and observer both are moving away from each other. So, by Doppler’s effect, observed frequency is given by
$$ f=f _0\left(\frac{v+v _o}{v-v _s}\right) \cdots(i) $$
where, $\quad v=$ speed of sound $=340 ms^{-1}$,
$$ v _o=\text { speed of observer }=-20 ms^{-1}, $$
$$ \begin{aligned} & v _s=\text { speed of source }=-20 ms^{-1}, \\ & f _0=\text { true frequency } \end{aligned} $$
and $\quad f=$ apparent frequency $=2000 Hz$
Substituting the given values in Eq. (i), we get
$$ \begin{aligned} 2000 & =\left(\frac{340-20}{340+20}\right) \times f _0 \\ \Rightarrow \quad f _0 & =\frac{2000 \times 360}{320}=2250 Hz \end{aligned} $$






