Wave Motion 4 Question 5
5. Two cars
(2019 Main, 9 April II)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- The given condition can be shown below as,
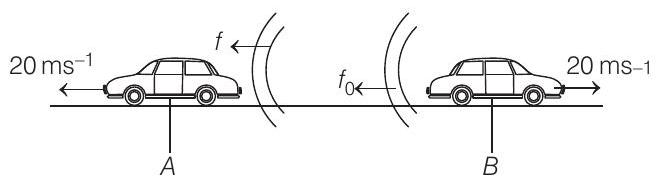
Here, source and observer both are moving away from each other. So, by Doppler’s effect, observed frequency is given by
where,
and
Substituting the given values in Eq. (i), we get






