Wave Motion 4 Question 29
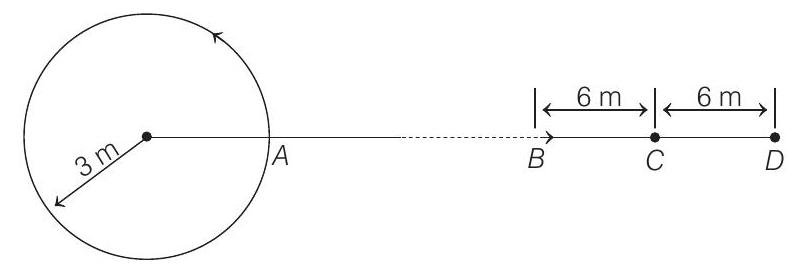
27. A source of sound is moving along a circular path of radius $3 m$ with an angular velocity of $10 rad / s$. A sound detector located far away from the source is executing linear simple harmonic motion along the line $B D$ (see figure) with an amplitude $B C=C D=6 m$. The frequency of oscillation of the detector is $5 / \pi$ per second. The source is at the point $A$ when the detector is at the point $B$. If the source emits a continuous sound wave of frequency $340 Hz$, find the maximum and the minimum frequencies recorded by the detector. (Speed of sound $=340 m / s$ )
(1990, 7M)
Show Answer
Answer:
Correct Answer: 27. 438.7 Hz to 257.3 Hz
Solution:
- Angular frequency of detector
$$ \omega=2 \pi f=2 \pi\left(\frac{5}{\pi}\right)=10 rad / s $$
Since, angular frequency of source of sound and of detector are equal, their time periods will also be equal.
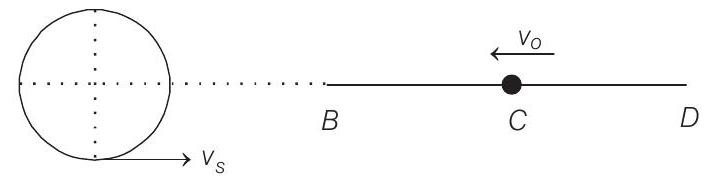
Maximum frequency will be heard in the position shown in figure. Since, the detector is far away from the source, we can use,
$$ f _{\max }=f\left(\frac{v+v _o}{v-v _s}\right) $$
Here, $v=$ speed of sound $=340 m / s$
(given)
$$ \begin{aligned} v _s & =R \omega=30 m / s \\ v _o & =\omega A=60 m / s \\ \therefore \quad f _{\max } & =340\left[\frac{340+60}{340-30}\right] \\ & =438.7 Hz \end{aligned} $$
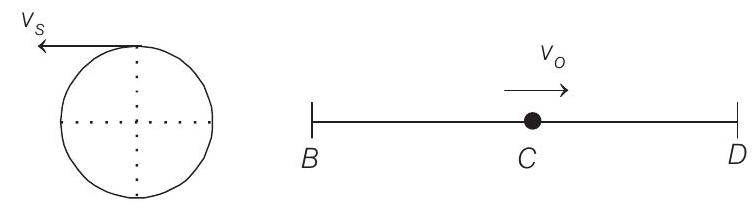
Minimum frequency will be heard in the condition shown in figure. The minimum frequency will be
$$ \begin{aligned} f _{\min } & =f\left[\frac{v-v _o}{v+v _s}\right]=340\left[\frac{340-60}{340+30}\right] \\ & =257.3 Hz \end{aligned} $$






