SATHEE: Wave Motion 3 Question 9

Wave Motion 3 Question 9

9. A long wire $P Q R$ is made by joining two wires $P Q$ and $Q R$ of equal radii. $P Q$ has length $4.8 m$ and mass $0.06 k g . Q R$ has length $2.56 m$ and mass $0.2 k g$ . The wire $P Q R$ is under a tension of $80 N$ . A sinusoidal wave pulse of amplitude $3.5 c m$ is sent along the wire $P Q$ from the end $P$ . No power is dissipated during the propagation of the wave pulse. Calculate

(1999, 10M)

(a) the time taken by the wave pulse to reach the other end $R$ and

(b) the amplitude of the reflected and transmitted wave pulse after the incident wave pulse crosses the joint $Q$ .

Show Answer

Answer:

Correct Answer: 9. (a) $0.14 s$ (b) $A_{r} = 1.5 c m$ and $A_{t} = 2.0 c m$

Solution:

Amplitude of incident wave $A_{i} = 3.5 c m$

Tension $T = 80 N$

Amplitude of incident wave $A_{i} = 3.5 c m$

Mass per unit length of wire $P Q$ is

$m_{1} = \frac{0.06}{4.8} = \frac{1}{80} k g / m$

and mass per unit length of wire $Q R$ is

$m_{2} = \frac{0.2}{2.56} = \frac{1}{12.8} k g / m$

(a) Speed of wave in wire $P Q$ is

$v_{1} = \sqrt{\frac{T}{m_{1}}} = \sqrt{\frac{80}{1 / 80}} = 80 m / s$

and speed of wave in wire

$\begin{aligned} Q R is v_{2} = \sqrt{\frac{T}{m_{2}}} & = \sqrt{\frac{80}{1 / 12.8}} \\ = 32 m / s \end{aligned}$

$∴$ Time taken by the wave pulse to reach from $P$ to $R$ is

$\begin{aligned} t = \frac{4.8}{v_{1}} + \frac{2.56}{v_{2}} = (\frac{4.8}{80} + \frac{2.56}{32}) s \\ t = 0.14 s \end{aligned}$

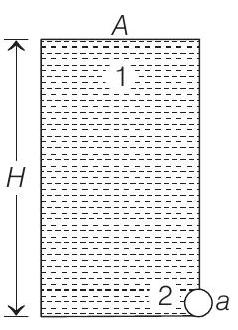
(b) The expressions for reflected and transmitted amplitudes ( $A_{r}$ and $A_{t}$ ) in terms of $v_{1}, v_{2}$ and $A_{i}$ are as follows :

$A_{r} = \frac{v_{2} - v_{1}}{v_{2} + v_{1}} A_{i} and A_{t} = \frac{2 v_{2}}{v_{1} + v_{2}} A_{i}$

Substituting the values, we get

$A_{r} = (\frac{32 - 80}{32 + 80}) (3.5) = - 1.5 c m$

i.e. the amplitude of reflected wave will be $1.5 c m$ . Negative sign of $A_{r}$ indicates that there will be a phase change of $π$ in reflected wave. Similarly,

$A_{t} = (\frac{2 \times 32}{32 + 80}) (3.5) = 2.0 c m$

i.e. the amplitude of transmitted wave will be $2.0 c m$ . NOTE The expressions of $A_{r}$ and $A_{t}$ are derived as below. Derivation

Suppose the incident wave of amplitude $A_{i}$ and angular frequency $ω$ is travelling in positive $x$ -direction with velocity $v_{1}$ then, we can write

$y_{i} = A_{i} \sin w [t - \frac{x}{v_{1}}]$

In reflected as well as transmitted wave, $ω$ will not change, therefore, we can write, and

$\begin{aligned} y_{r} = A_{r} \sin ω [t + \frac{x}{v_{1}}] \\ y_{t} = A_{t} \sin ω [t - \frac{x}{v_{2}}] \end{aligned}$

Now, as wave is continuous, so at the boundary $(x = 0)$ .

Continuity of displacement requires

Substituting, we get

$y_{i} + y_{r} = y_{t} for (x = 0)$

$A_{i} + A_{r} = A_{t}$

Also at the boundary, slope of wave will be continuous i.e.,

$\frac{\partial y_{i}}{\partial x} + \frac{\partial y_{r}}{\partial x} = \frac{\partial y_{t}}{\partial x}$

for $x = 0$

Which gives,

$A_{i} - A_{r} = (\frac{v_{1}}{v_{2}}) A_{t}$

Solving Eqs. (iv) and (v) for $A_{r}$ and $A_{t}$ , we get the required equations i.e.

$\begin{aligned} A_{r} = \frac{v_{2} - v_{1}}{v_{2} + v_{1}} A_{i} \\ and & A_{t} = \frac{2 v_{2}}{v_{2} + v_{1}} A_{i} \end{aligned}$

Wave Motion 3 Question 9

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Wave Motion 3 Question 9

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu