Wave Motion 3 Question 9
9. A long wire $P Q R$ is made by joining two wires $P Q$ and $Q R$ of equal radii. $P Q$ has length $4.8 m$ and mass $0.06 kg . Q R$ has length $2.56 m$ and mass $0.2 kg$. The wire $P Q R$ is under a tension of $80 N$. A sinusoidal wave pulse of amplitude $3.5 cm$ is sent along the wire $P Q$ from the end $P$. No power is dissipated during the propagation of the wave pulse. Calculate
(1999, 10M)
(a) the time taken by the wave pulse to reach the other end $R$ and
(b) the amplitude of the reflected and transmitted wave pulse after the incident wave pulse crosses the joint $Q$.
Show Answer
Answer:
Correct Answer: 9. (a) $0.14 s \quad$ (b) $A _r=1.5 cm$ and $A _t=2.0 cm$
Solution:
- Amplitude of incident wave $A _i=3.5 cm$
Tension $T=80 N$
Amplitude of incident wave $A _i=3.5 cm$
Mass per unit length of wire $P Q$ is
$$ m _1=\frac{0.06}{4.8}=\frac{1}{80} kg / m $$
and mass per unit length of wire $Q R$ is
$$ m _2=\frac{0.2}{2.56}=\frac{1}{12.8} kg / m $$
(a) Speed of wave in wire $P Q$ is
$$ v _1=\sqrt{\frac{T}{m _1}}=\sqrt{\frac{80}{1 / 80}}=80 m / s $$
and speed of wave in wire
$$ \begin{aligned} Q R \text { is } v _2=\sqrt{\frac{T}{m _2}} & =\sqrt{\frac{80}{1 / 12.8}} \\ & =32 m / s \end{aligned} $$
$\therefore$ Time taken by the wave pulse to reach from $P$ to $R$ is
$$ \begin{aligned} & t=\frac{4.8}{v _1}+\frac{2.56}{v _2}=\left(\frac{4.8}{80}+\frac{2.56}{32}\right) s \\ & t=0.14 s \end{aligned} $$
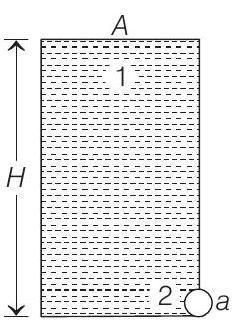
(b) The expressions for reflected and transmitted amplitudes ( $A _r$ and $A _t$ ) in terms of $v _1, v _2$ and $A _i$ are as follows :
$$ A _r=\frac{v _2-v _1}{v _2+v _1} A _i \quad \text { and } \quad A _t=\frac{2 v _2}{v _1+v _2} A _i $$
Substituting the values, we get
$$ A _r=\left(\frac{32-80}{32+80}\right)(3.5)=-1.5 cm $$
i.e. the amplitude of reflected wave will be $1.5 cm$. Negative sign of $A _r$ indicates that there will be a phase change of $\pi$ in reflected wave. Similarly,
$$ A _t=\left(\frac{2 \times 32}{32+80}\right)(3.5)=2.0 cm $$
i.e. the amplitude of transmitted wave will be $2.0 cm$. NOTE The expressions of $A _r$ and $A _t$ are derived as below. Derivation
Suppose the incident wave of amplitude $A _i$ and angular frequency $\omega$ is travelling in positive $x$-direction with velocity $v _1$ then, we can write
$$ y _i=A _i \sin w\left[t-\frac{x}{v _1}\right] $$
In reflected as well as transmitted wave, $\omega$ will not change, therefore, we can write, and
$$ \begin{aligned} & y _r=A _r \sin \omega\left[t+\frac{x}{v _1}\right] \\ & y _t=A _t \sin \omega\left[t-\frac{x}{v _2}\right] \end{aligned} $$
Now, as wave is continuous, so at the boundary $(x=0)$.
Continuity of displacement requires
Substituting, we get
$$ y _i+y _r=y _t \text { for }(x=0) $$
$$ A _i+A _r=A _t $$
Also at the boundary, slope of wave will be continuous i.e.,
$$ \frac{\partial y _i}{\partial x}+\frac{\partial y _r}{\partial x}=\frac{\partial y _t}{\partial x} $$
for $\quad x=0$
Which gives,
$$ A _i-A _r=\left(\frac{v _1}{v _2}\right) A _t $$
Solving Eqs. (iv) and (v) for $A _r$ and $A _t$, we get the required equations i.e.
$$ \begin{aligned} & A _r=\frac{v _2-v _1}{v _2+v _1} A _i \\ \text { and } \quad & A _t=\frac{2 v _2}{v _2+v _1} A _i \end{aligned} $$
