Wave Motion 2 Question 5
5. A resonance tube is old and has jagged end. It is still used in the laboratory to determine velocity of sound in air. A tuning fork of frequency $512 Hz$ produces first resonance when the tube is filled with water to a mark $11 cm$ below a reference mark. near the open end of the tube. The experiment is repeated with another fork of frequency $256 Hz$ which produces first resonance when water reaches a mark $27 cm$ below the reference mark. The velocity of sound in air, obtained in the experiment is close to
(Main 2019, 12 Jan II)
(a) $328 ms^{-1}$ (b)
(b) $341 ms^{-1}$
(c) $322 ms^{-1}$
(d) $335 ms^{-1}$
Show Answer
Answer:
Correct Answer: 5. (a)
Solution:
- Key idea
To overcome the error occured in measurement of resonant length. We introduce end correction factor $e$ in length.
In first resonance, length of air coloumn $=\frac{\lambda}{4}$.
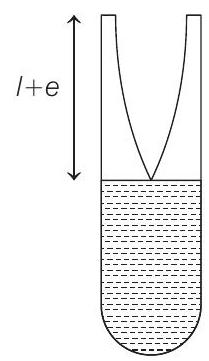
So, $\quad l _1+e=\frac{\lambda}{4}$ or $11 \times 4+4 e=\lambda$
So, speed of sound is
$$ \Rightarrow \quad v=f _1 \lambda=512(44+4 e) \cdots(i) $$
And in second case,
$$ \begin{array}{cc} & l _1^{\prime}+e=\frac{\lambda^{\prime}}{4} \text { or } 27 \times 4+4 e=\lambda^{\prime} \\ \Rightarrow \quad & v=f _2 \lambda^{\prime}=256(108+4 e) \cdots(ii) \end{array} $$
Dividing both Eqs. (i) and (ii), we get
$$ 1=\frac{512(44+4 e)}{256(108+4 e)} \Rightarrow e=5 cm $$
Substituting value of $e$ in Eq. (i), we get
Speed of sound $v=512(44+4 e)$
$$ \begin{aligned} & =512(44+4 \times 5) \\ & =512 \times 64 cm s^{-1}=327.68 ms^{-1} \approx 328 ms^{-1} \end{aligned} $$






