Wave Motion 1 Question 4
4. A heavy ball of mass $M$ is suspended from the ceiling of a car by a light string of mass $m(m«M)$. When the car is at rest, the speed of transverse waves in the string is $60 ms^{-1}$. When the car has acceleration $a$, the wave speed increases to $60.5 ms^{-1}$. The value of $a$, in terms of gravitational acceleration $g$ is closest to
(2019 Main, 9 Jan I)
(a) $\frac{g}{20}$
(b) $\frac{g}{5}$
(c) $\frac{g}{30}$
(d) $\frac{g}{10}$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- When the car is at rest, then the situation can be shown in the figure below.
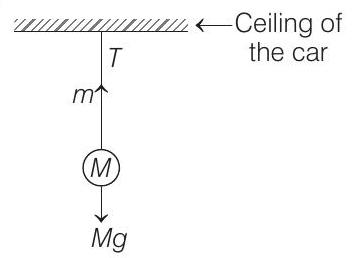
Since, $m«M$, then we can neglect the mass of the string. So, the initial velocity of the wave in the string can be given as,
$$ v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{M g}{\frac{M}{l}}}=60 m / s $$
where, $T$ is the tension in the string and $\mu$ is the mass of the block per unit length $(l)$.
Now, when the car has acceleration ’ $a$ ‘, then the situation can be shown in the figure given below,
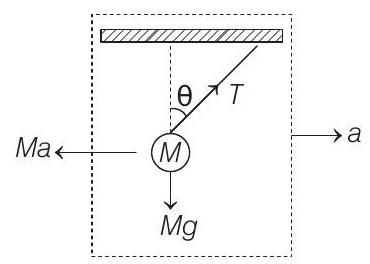
Resolving the components of ’ $T$ ’ along $X$-and $Y$-axis, we get
$$ \begin{aligned} T \cos \theta & =M g \\ T \sin \theta & =M a \end{aligned} $$
Squaring both sides of Eqs. (ii) and (iii) and adding them, we get
$$ \begin{array}{cc} & T^{2}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)=M^{2}\left(g^{2}+a^{2}\right) \\ \Rightarrow \quad T=M\left(g^{2}+a^{2}\right)^{\frac{1}{2}} \end{array} $$
Now, the velocity of the wave in the string would be given as,
$$ v^{\prime}=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{M\left(g^{2}+a^{2}\right)^{\frac{1}{2}}}{\frac{M}{l}}}=60.5 m / s $$
Dividing Eq. (i) and Eq. (v), we get
$$ \frac{v}{v^{\prime}}=\frac{\sqrt{\frac{\frac{M g}{l}}{l}}}{\sqrt{\frac{M\left(g^{2}+a^{2}\right)^{\frac{1}{2}}}{\frac{M}{l}}}}=\sqrt{\frac{g}{\left(g^{2}+a^{2}\right)^{\frac{1}{2}}}}=\frac{60}{60.5} $$
or
$$ \frac{60.5}{60}=\sqrt{\frac{\left(g^{2}+a^{2}\right)^{\frac{1}{2}}}{g}} $$
Squaring both the sides, we get
$\begin{aligned} \frac{(60.5)^{2}}{(60)^{2}} & =\frac{\left(g^{2}+a^{2}\right)^{\frac{1}{2}}}{g} \ \left(1+\frac{0.5}{60}\right)^{2} & =\sqrt{1+\left(\frac{a}{g}\right)^{2}}\end{aligned}$
Using binomial expansion,
$$ (1+x)^{n}=1+\frac{n x}{1 !}+\ldots $$
On both sides, we get
$$ \begin{gathered} 1+2 \times \frac{0.5}{60}=1+\frac{1}{2} \cdot \frac{a^{2}}{g^{2}} \\ \Rightarrow 1+\frac{1}{60}=1+\frac{1}{2} \cdot \frac{a^{2}}{g^{2}} \quad \text { or } \quad \frac{a}{g}=\frac{1}{\sqrt{30}} \\ \text { or } \quad a=\frac{g}{\sqrt{30}}=\frac{g}{5.4} \simeq \frac{g}{5} \end{gathered} $$






