Wave Motion 1 Question 1
1. A progressive wave travelling along the positive $x$-direction is represented by $y(x, t)=A \sin (k x-\omega t+\phi)$. Its snapshot at $t=0$ is given in the figure.
(2019 Main, 12 April I)
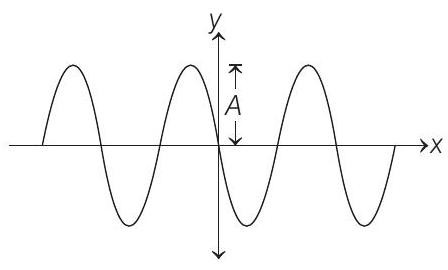
For this wave, the phase $\phi$ is
(a) $-\frac{\pi}{2}$
(b) $\pi$
(c) 0
(d) $\frac{\pi}{2}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- From the given snapshot at $t=0$,
$$ y=0 \text { at } x=0 $$
and $y=-\operatorname{ve}$ when $x$ increases from zero.
Standard expression of any progressive wave is given by $y=A \sin (k x-\omega t+\phi)$
Here, $\phi$ is the phase difference, we need to get
at $\quad t=0 \quad y=A \sin (k x+\phi)$
Clearly $\phi=\pi$, so that
$$ \begin{aligned} & & y=A \sin (k x+\pi) \\ \Rightarrow & & y=-A \sin (k x) \\ \text { and } & y & =0 \text { at } x=0 \\ & y & =- \text { ve at } x>0 \end{aligned} $$






