SATHEE: Wave Motion 1 Question 1

Wave Motion 1 Question 1

1. A progressive wave travelling along the positive $x$ -direction is represented by $y (x, t) = A \sin (k x - ω t + ϕ)$ . Its snapshot at $t = 0$ is given in the figure.

(2019 Main, 12 April I)

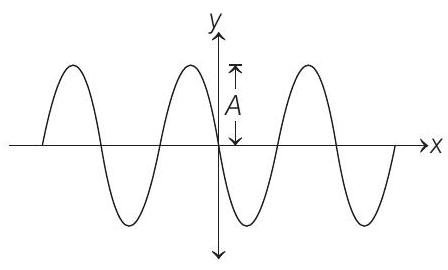
For this wave, the phase $ϕ$ is

(a) $- \frac{π}{2}$

(b) $π$

(d) $\frac{π}{2}$

Show Answer

Answer:

Correct Answer: 1. (b)

Solution:

From the given snapshot at $t = 0$ ,

$y = 0 at x = 0$

and $y = - ve$ when $x$ increases from zero.

Standard expression of any progressive wave is given by $y = A \sin (k x - ω t + ϕ)$

Here, $ϕ$ is the phase difference, we need to get

at $t = 0 y = A \sin (k x + ϕ)$

Clearly $ϕ = π$ , so that

$\begin{aligned} y = A \sin (k x + π) \\ \Rightarrow & y = - A \sin (k x) \\ and & y & = 0 at x = 0 \\ y & = - ve at x > 0 \end{aligned}$

पिछला

अगला

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in

SATHEE का मीडिया कवरेज

खेल स्टोर

ऐप स्टोर

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Wave Motion 1 Question 1

1. A progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin⁡(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

1. A progressive wave travelling along the positive $x$ -direction is represented by $y (x, t) = A \sin (k x - ω t + ϕ)$ . Its snapshot at $t = 0$ is given in the figure.