Simple Harmonic Motion 5 Question 21
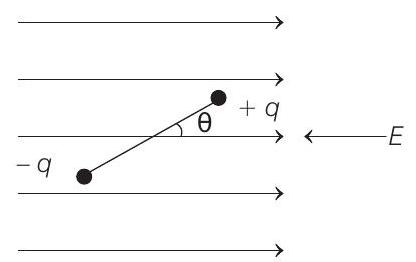
26. A point particle of mass $M$ attached to one end of a massless rigid non- conducting rod of length $L$. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges $+q$ and $-q$ respectively. This arrangement is held in a region of a uniform electric field $E$ such that the rod makes a small angle $\theta$ (say of about 5 degrees) with the field direction. Find an expression for the minimum time needed for the rod to become parallel to the field after it is set free. $(1989,8 M)$
Show Answer
Answer:
Correct Answer: 26. $\frac{\pi}{2} \sqrt{\frac{M L}{2 q E}}$
Solution:
- A torque will act on the rod, which tries to align the rod in the direction of electric field. This torque will be of restoring nature and has a magnitude $P E \sin \theta$. Therefore, we can write
$$ \tau=-P E \sin \theta \quad \text { or } \quad I \alpha=-P E \sin \theta $$
Here, $\quad I=2 M \quad \frac{L^{2}}{2}=\frac{M L^{2}}{2}$ and $P=q L$ Further, since $\theta$ is small so, we can write, $\sin \theta \approx \theta$.
Substituting these values in Eq. (i), we have
$$ \frac{M L^{2}}{2} \alpha=-(q L)(E) \theta $$
or
$$ \alpha=-\frac{2 q E}{M L} \theta $$
As $\alpha$ is proportional to $-\theta$, motion of the rod is simple harmonic in nature, time period of which is given by
$$ T=2 \pi \sqrt{\left|\frac{\theta}{\alpha}\right|}=2 \pi \sqrt{\frac{M L}{2 q E}} $$
The desired time will be,
$$ t=\frac{T}{4}=\frac{\pi}{2} \sqrt{\frac{M L}{2 q E}} $$
Download Chapter Test http://tinyurl.com/y455aoqv






