Simple Harmonic Motion 5 Question 21

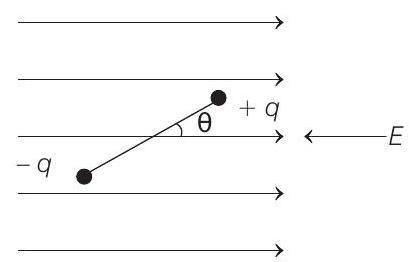
26. A point particle of mass M attached to one end of a massless rigid non- conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and −q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degrees) with the field direction. Find an expression for the minimum time needed for the rod to become parallel to the field after it is set free. (1989,8M)

Show Answer

Answer:

Correct Answer: 26. π2ML2qE

Solution:

  1. A torque will act on the rod, which tries to align the rod in the direction of electric field. This torque will be of restoring nature and has a magnitude PEsin⁡θ. Therefore, we can write

τ=−PEsin⁡θ or Iα=−PEsin⁡θ

Here, I=2ML22=ML22 and P=qL Further, since θ is small so, we can write, sin⁡θ≈θ.

Substituting these values in Eq. (i), we have

ML22α=−(qL)(E)θ

or

α=−2qEMLθ

As α is proportional to −θ, motion of the rod is simple harmonic in nature, time period of which is given by

T=2π|θα|=2πML2qE

The desired time will be,

t=T4=π2ML2qE

Download Chapter Test http://tinyurl.com/y455aoqv

9

इंजीनियरिंग की तैयारी

रसायन विज्ञान 11वीं

रसायन विज्ञान 12वीं

गणित 11वीं

गणित 12वीं

भौतिक विज्ञान 11वीं

भौतिक विज्ञान 12वीं

जेईई पिछले वर्ष के प्रश्न

जेईई ट्यूटोरियल सत्र

चिकित्सा तैयारी

जीव विज्ञान 11वीं

जीव विज्ञान 12वीं

रसायन विज्ञान 11वीं

रसायन विज्ञान 12वीं

भौतिक विज्ञान 11वीं

भौतिक विज्ञान 12वीं

एनईईटी पिछले वर्ष के प्रश्न

एनईईटी ट्यूटोरियल सत्र

एनसीईआरटी पुस्तकें और समाधान

जेईई के लिए एनसीईआरटी पुस्तकें

एनईईटी के लिए एनसीईआरटी पुस्तकें

जेईई के लिए एनसीईआरटी समाधान

एनईईटी के लिए एनसीईआरटी समाधान

जेईई के लिए एनसीईआरटी एक्जम्पलर

एनईईटी के लिए एनसीईआरटी एक्जम्पलर

9वीं के लिए एनसीईआरटी किताबें

10वीं के लिए एनसीईआरटी किताबें

9वीं-10वीं के लिए एनसीईआरटी एक्जम्पलर

महत्वपूर्ण संसाधन

भौतिक विज्ञान फॉर्मूला

रसायन विज्ञान फॉर्मूला

गणित के फॉर्मूला

उपयोगी लेख

अन्य संसाधन

मीडिया कवरेज

सहायता वीडियो

शैक्षिक खेल

10वीं और 12वीं बोर्ड परीक्षा के लिए

GK

सामयिक घटनाएँ

पंचांग

पाठ्यक्रम

जेईई पाठ्यक्रम

ऐनईईटी पाठ्यक्रम

परीक्षा मंच

जेईई / इंजीनियरिंग टेस्ट

एनईईटी/मेडिकल टेस्ट

नमूना मॉक टेस्ट

जेईई के लिए मॉक टेस्ट

सदस्यता

जेईई के लिए मेंटरशिप

एनईईटी के लिए मेंटरशिप

एनसीईआरटी व्यायाम वीडियो समाधान

एनसीईआरटी अध्याय वीडियो समाधान

दोहरा फलक

© 2024 कॉपीराइट SATHEE

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in
SATHEE का मीडिया कवरेज
goolge

खेल स्टोर
goolge

ऐप स्टोर