Simple Harmonic Motion 5 Question 16
21. Two independent harmonic oscillators of equal masses are oscillating about the origin with angular frequencies $\omega _1$ and $\omega _2$ and have total energies $E _1$ and $E _2$, respectively. The variations of their momenta $p$ with positions $x$ are shown in the figures. If $\frac{a}{b}=n^{2}$ and $\frac{a}{R}=n$, then the correct equations is/are
(2015 Adv.)
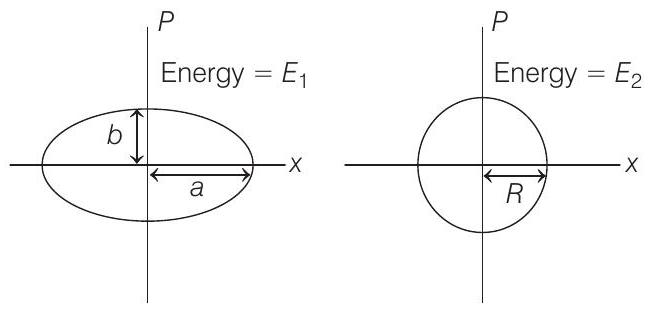
(a) $E _1 \omega _1=E _2 \omega _2$
(b) $\frac{\omega _2}{\omega _1}=n^{2}$
(c) $\omega _1 \omega _2=n^{2}$
(d) $\frac{E _1}{\omega _1}=\frac{E _2}{\omega _2}$
Show Answer
Answer:
Correct Answer: 21. (b, d)
Solution:
- Ist Particle
$$ P=0 \text { at } x=a $$
$\Rightarrow \quad$ ’ $a$ ’ is the amplitude of oscillation ’ $A _1$ ‘.
$$ \begin{aligned} \Rightarrow \quad \text { At } x & =0, P=b \quad \text { (at mean position) } \\ m v _{\max } & =b \\ v _{\max } & =\frac{b}{m} \\ E _1 & =\frac{1}{2} m v _{\max }^{2}=\frac{m}{2} \frac{b^{2}}{m}=\frac{b^{2}}{2 m} \\ A _1 \omega _1 & =v _{\max }=\frac{b}{m} \\ \quad \omega _1 & =\frac{b}{m a}=\frac{1}{m n^{2}}\left(A _1=a, \frac{a}{b}=n^{2}\right) \end{aligned} $$
IInd Particle
$$ \begin{array}{rlrl} \Rightarrow & & P & =0 \text { at } x=R \\ \text { At } & & A _2 & =R \\ \Rightarrow & x & =0, P=R \\ & & v _{\max } & =\frac{R}{m} \\ & & E _2 & =\frac{1}{2} m v _{\max }^{2}=\frac{m}{2} \frac{R^{2}}{m}=\frac{R^{2}}{2 m} \\ \Rightarrow & & A _2 \omega _2 & =\frac{R}{m} \\ & & \omega _2 & =\frac{R}{m R}=\frac{1}{m} \end{array} $$
(b) $\frac{\omega _2}{\omega _1}=\frac{1 / m}{1 / m n^{2}}=n^{2}$
(c) $\omega _1 \omega _2=\frac{1}{m n^{2}} \times \frac{1}{m}=\frac{1}{m^{2} n^{2}}$
(d) $\frac{E _1}{\omega _1}=\frac{b^{2} / 2 m}{1 / m n^{2}}=\frac{b^{2} n^{2}}{2}=\frac{a^{2}}{2 n^{2}}=\frac{R^{2}}{2}$
$$ \begin{aligned} & \frac{E _2}{\omega _2}=\frac{R^{2} / 2 m}{1 / m}=\frac{R^{2}}{2} \\ & \Rightarrow \quad \frac{E _1}{\omega _1}=\frac{E _2}{\omega _2} \end{aligned} $$
NOTE
It is not given that the second figure is a circle. But from the figure and as per the requirement of question, we consider it is a circle.






