SATHEE: Simple Harmonic Motion 5 Question 16

Simple Harmonic Motion 5 Question 16

21. Two independent harmonic oscillators of equal masses are oscillating about the origin with angular frequencies $ω_{1}$ and $ω_{2}$ and have total energies $E_{1}$ and $E_{2}$ , respectively. The variations of their momenta $p$ with positions $x$ are shown in the figures. If $\frac{a}{b} = n^{2}$ and $\frac{a}{R} = n$ , then the correct equations is/are

(2015 Adv.)

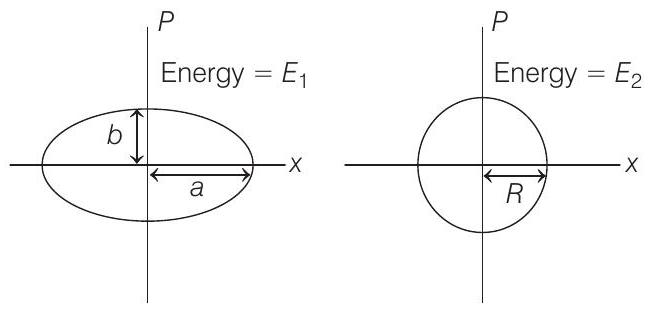
(a) $E_{1} ω_{1} = E_{2} ω_{2}$

(b) $\frac{ω_{2}}{ω_{1}} = n^{2}$

(d) $\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$

Show Answer

Answer:

Correct Answer: 21. (b, d)

Solution:

Ist Particle

$P = 0 at x = a$

$\Rightarrow$ ’ $a$ ’ is the amplitude of oscillation ’ $A_{1}$ ‘.

$\begin{aligned} \Rightarrow At x & = 0, P = b (at mean position) \\ m v_{max} & = b \\ v_{max} & = \frac{b}{m} \\ E_{1} & = \frac{1}{2} m v_{max}^{2} = \frac{m}{2} \frac{b^{2}}{m} = \frac{b^{2}}{2 m} \\ A_{1} ω_{1} & = v_{max} = \frac{b}{m} \\ ω_{1} & = \frac{b}{m a} = \frac{1}{m n^{2}} (A_{1} = a, \frac{a}{b} = n^{2}) \end{aligned}$

IInd Particle

$\begin{aligned} \Rightarrow & P & = 0 at x = R \\ At & A_{2} & = R \\ \Rightarrow & x & = 0, P = R \\ v_{max} & = \frac{R}{m} \\ E_{2} & = \frac{1}{2} m v_{max}^{2} = \frac{m}{2} \frac{R^{2}}{m} = \frac{R^{2}}{2 m} \\ \Rightarrow & A_{2} ω_{2} & = \frac{R}{m} \\ ω_{2} & = \frac{R}{m R} = \frac{1}{m} \end{aligned}$

(b) $\frac{ω_{2}}{ω_{1}} = \frac{1 / m}{1 / m n^{2}} = n^{2}$

(d) $\frac{E_{1}}{ω_{1}} = \frac{b^{2} / 2 m}{1 / m n^{2}} = \frac{b^{2} n^{2}}{2} = \frac{a^{2}}{2 n^{2}} = \frac{R^{2}}{2}$

$\begin{aligned} \frac{E_{2}}{ω_{2}} = \frac{R^{2} / 2 m}{1 / m} = \frac{R^{2}}{2} \\ \Rightarrow \frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}} \end{aligned}$