Simple Harmonic Motion 3 Question 6
6. The period of oscillation of simple pendulum of length $L$ suspended from the roof of the vehicle which moves without friction, down an inclined plane of inclination $\alpha$, is given by
(a) $2 \pi \sqrt{\frac{L}{g \cos \alpha}}$
(b) $2 \pi \sqrt{\frac{L}{g \sin \alpha}}$
(c) $2 \pi \sqrt{\frac{L}{g}}$
(d) $2 \pi \sqrt{\frac{L}{g \tan \alpha}}$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- Free body diagram of bob of the pendulum with respect to the accelerating frame of reference is as follows
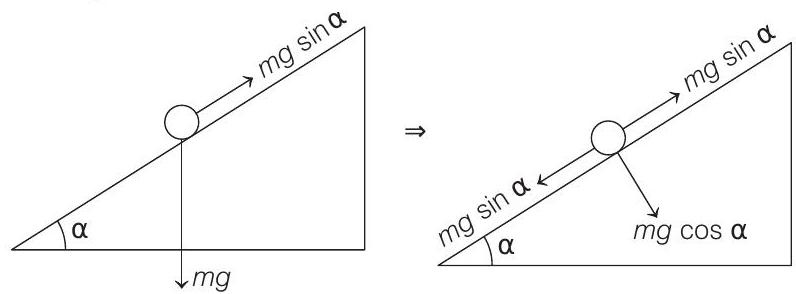
$\therefore$ Net force on the bob is $F _{\text {net }}=m g \cos \alpha$ or net acceleration of the bob is $g _{\text {eff }}=g \cos \alpha$
or
$$ T=2 \pi \sqrt{\frac{L}{g _{\text {eff }}}} $$
NOTE
- Whenever point of suspension is accelerating
$$ \text { Take, } \quad T=2 \pi \sqrt{\frac{L}{g _{\text {eff }}}} $$
where, $g _{\text {eff }}=g-a$
$\mathbf{a}=$ acceleration of point of suspension.
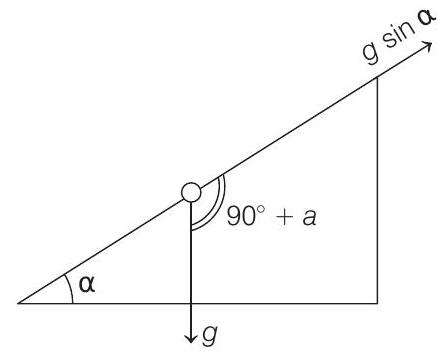
In this question, $a=g \sin \alpha$ (down the plane)
$$ \begin{aligned} & \quad|g-a|=g _{\text {eff }} \\ & =\sqrt{g^{2}+(g \sin \alpha)^{2}+2(g)(g \sin \alpha) \cos \left(90^{\circ}+\alpha\right)} \\ & =g \cos \alpha \end{aligned} $$






