SATHEE: Simple Harmonic Motion 3 Question 6

Simple Harmonic Motion 3 Question 6

6. The period of oscillation of simple pendulum of length $L$ suspended from the roof of the vehicle which moves without friction, down an inclined plane of inclination $α$ , is given by

(a) $2 π \sqrt{\frac{L}{g \cos α}}$

(b) $2 π \sqrt{\frac{L}{g \sin α}}$

(d) $2 π \sqrt{\frac{L}{g \tan α}}$

Show Answer

Answer:

Correct Answer: 6. (a)

Solution:

Free body diagram of bob of the pendulum with respect to the accelerating frame of reference is as follows

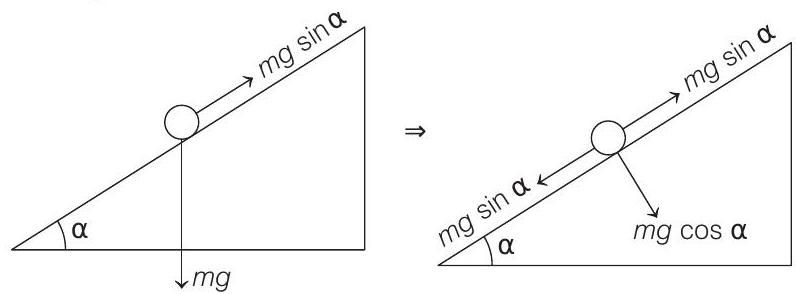
$∴$ Net force on the bob is $F_{net} = m g \cos α$ or net acceleration of the bob is $g_{eff} = g \cos α$

$T = 2 π \sqrt{\frac{L}{g_{eff}}}$

NOTE

Whenever point of suspension is accelerating

$Take, T = 2 π \sqrt{\frac{L}{g_{eff}}}$

where, $g_{eff} = g - a$

$a =$ acceleration of point of suspension.

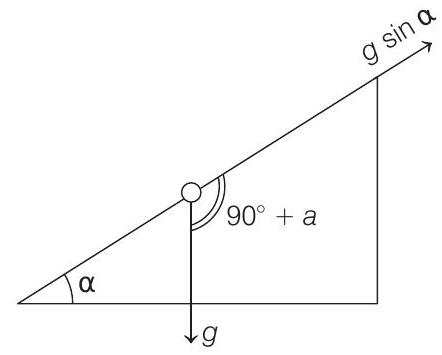
In this question, $a = g \sin α$ (down the plane)

$\begin{aligned} | g - a | = g_{eff} \\ = \sqrt{g^{2} + (g \sin α)^{2} + 2 (g) (g \sin α) \cos (90^{\circ} + α)} \\ = g \cos α \end{aligned}$

पिछला

अगला

Simple Harmonic Motion 3 Question 6

6. The period of oscillation of simple pendulum of length $L$ suspended from the roof of the vehicle which moves without friction, down an inclined plane of inclination $α$ , is given by

Answer:

NOTE

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Simple Harmonic Motion 3 Question 6

6. The period of oscillation of simple pendulum of length L suspended from the roof of the vehicle which moves without friction, down an inclined plane of inclination α, is given by

Answer:

NOTE

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

6. The period of oscillation of simple pendulum of length $L$ suspended from the roof of the vehicle which moves without friction, down an inclined plane of inclination $α$ , is given by