Simple Harmonic Motion 3 Question 12
12. A thin fixed ring of radius $1 m$ has a positive charge $1 \times 10^{-5} C$ uniformly distributed over it. A particle of mass $0.9 g$ and having a negative charge of $1 \times 10^{-6} C$ is placed on the axis at a distance of $1 cm$ from the centre of the ring. Show that the motion of the negatively charged particle is approximately simple harmonic. Calculate the time period of oscillations.
(1982, 5M)
Show Answer
Answer:
Correct Answer: 12. $0.628 s$
Solution:
- Given, $Q=10^{-5} C$
$$ \begin{aligned} q & =10^{-6} C, \quad R=1 m \\ \text { and } \quad m & =9 \times 10^{-4} kg \end{aligned} $$
Electric field at a distance $x$ from the centre on the axis of a ring is given by
$$ E=\frac{1}{4 \pi \varepsilon _0} \frac{Q x}{\left(R^{2}+x^{2}\right)^{3 / 2}} $$
If $x«R, R^{2}+x^{2} \approx R^{2}$ and $E \approx \frac{Q x}{4 \pi \varepsilon _0 R^{3}}$
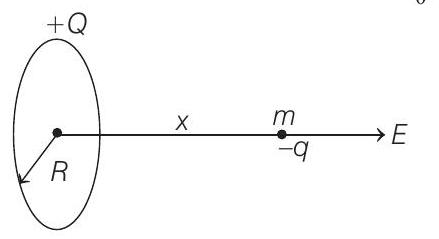
Net force on negatively charged particle would be $q E$ and towards the centre of ring. Hence, we can write
$$ \begin{aligned} F & =-\frac{Q q x}{\left(4 \pi \varepsilon _0\right) R^{3}} \\ \text { or } \quad \text { acceleration } a & =\frac{F}{m}=-\frac{Q q x}{\left(4 \pi \varepsilon _0\right) m R^{3}} \end{aligned} $$
as $a \propto-x$, motion of the particle is simple harmonic in nature. Time period of which will be given by
$$ T=2 \pi \sqrt{\left|\frac{x}{a}\right|} \text { or } T=2 \pi \sqrt{\frac{\left(4 \pi \varepsilon _0\right) m R^{3}}{Q q}} $$
Substituting the values, we get
$$ \begin{aligned} T & =2 \pi \sqrt{\frac{\left(9 \times 10^{-4}\right)(1)^{3}}{\left(9 \times 10^{9}\right)\left(10^{-5}\right)\left(10^{-6}\right)}} \\ & =0.628 s \end{aligned} $$






