Simple Harmonic Motion 3 Question 12
12. A thin fixed ring of radius
(1982, 5M)
Show Answer
Answer:
Correct Answer: 12.
Solution:
- Given,
Electric field at a distance
If
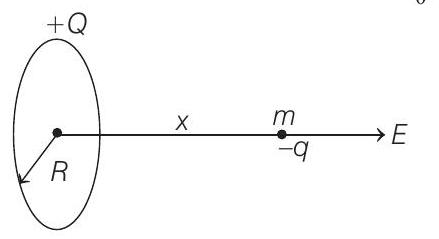
Net force on negatively charged particle would be
as
Substituting the values, we get






