Simple Harmonic Motion 3 Question 11
11. A thin rod of length $L$ and uniform cross-section is pivoted at its lowest point $P$ inside a stationary homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through $P$.
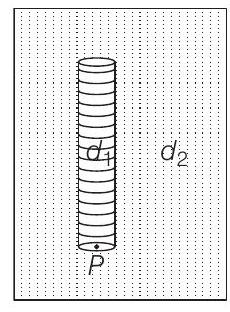
The density $d _1$ of the material of the rod is smaller than the density $d _2$ of the liquid. The rod is displaced by small angle $\theta$ from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
$(1996,5$ M)
Show Answer
Answer:
Correct Answer: 11. $\omega=\sqrt{\frac{3 g\left(d _2-d _1\right)}{2 d _1 L}}$
Solution:
- Let $S$ be the area of cross-section of the rod. In the displaced position, as shown in figure, weight $(w)$ and upthrust $\left(F _B\right)$ both pass through its centre of gravity $G$. Here, $w=($ volume $)$ (density of rod)
$$ g=(S L)\left(d _1\right) g $$
$F _B=($ Volume) (density of liquid) $g$
$$ =(S L)\left(d _2\right) g $$
Given that, $d _1<d _2$. Therefore, $w<F _B$ Therefore, net force acting at $G$ will be
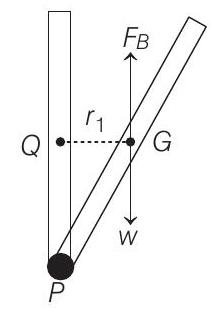
$$ \begin{aligned} & F=F _B-w=(S L g)\left(d _2-d _1\right) \quad \text { upwards. Restoring } \\ & \text { torque of this force about point } P \text { is } \\ & \quad \tau=F \times r _{\perp}=(S L g)\left(d _2-d _1\right)(Q G) \\ & \text { or } \quad \tau=-(S L g)\left(d _2-d _1\right) \frac{L}{2} \sin \theta \end{aligned} $$
Here, negative sign shows the restoring nature of torque.
$$ \text { or } \quad \tau=-\frac{S L^{2} g\left(d _2-d _1\right)}{2} \theta $$
$\sin \theta \approx \theta$ for small values of $\theta$
From Eq. (i), we see that $\tau \propto-\theta$
Hence, motion of the rod will be simple harmonic.
Rewriting Eq. (i) as
$$ I \frac{d^{2} \theta}{d t^{2}}=-\frac{S L^{2} g\left(d _2-d _1\right)}{2} \theta $$
Here, $I=$ moment of inertia of rod about an axis passing through $P$.
$$ I=\frac{M L^{2}}{3}=\frac{\left(S L d _1\right) L^{2}}{3} $$
Substituting this value of $I$ in Eq. (ii), we have
$$ \frac{d^{2} \theta}{d t^{2}}=-\frac{3}{2} \frac{g\left(d _2-d _1\right)}{d _1 L} \theta $$
Comparing this equation with standard differential equation of SHM, i.e. $\frac{d^{2} \theta}{d t^{2}}=-\omega^{2} \theta$
The angular frequency of oscillation is
$$ \omega=\sqrt{\frac{3 g\left(d _2-d _1\right)}{2 d _1 L}} $$






